自动搬运

查看原文

来自洛谷，原作者为

	llmmkk vanitas vanitatum

搬运于2025-08-24 22:17:10，当前版本为作者最后更新于2021-05-11 10:38:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

链接：P6075

---

前言：

虽然其他大佬们的走分界线的方法比我巧妙多了，但还是提供一种思路。

---

题意：

%&￥……@#直接看题面理解罢。

---

分析过程：

看到这样的题面我脑里第一反应就是DP，但是看到n和k的范围只能作罢。想到各种柿子又根本推不出来，于是颓废地打了个复杂度算不来的貌似是 $2^{n^3}$ 的深搜。于是有以下测试：

input      output

1 2         4

2 2         16

3 2         64

1 3         8

2 3         64

3 3        512

于是我们惊喜地发现答案貌似就是$2^{kn}$。但这个答案到底是怎么来的呢？

---

证明：

我们发现对这道题，所谓集合是可以拆解成n个元素分别处理的，可将其视为从三角形左上角起向右下进行连续的覆盖，如图：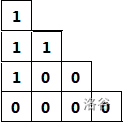

那么设一个元素在大小为k的三角形内的覆盖方案数为 $f(k)$ ，那么n个元素的方案总数即为 $f(k)^n$ 。接下来来推 $f(k)$ ，注意以下推理仍只关注一个元素。

对于一个大小为k的三角形，我们着重分析最下面一行，因为去掉这一行就能转化为更小的三角形，将覆盖，未覆盖以及任意取值分别看做“1”，“0”，和“？”，那么根据题意，这一行的状况只能是前面m个1，后面k-m个0，分情况讨论。

• 如果这行全部为零，即 ：

发现当前的方案数即为上面未确定三角形的方案数$f(k-1)$。

• 如果前面有 m $(1\le m< k-1 )$ 个1，即：

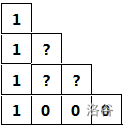
发现当前的方案数即为右上角缺失的三角形的方案数$f(k-1-m)$。

• 如果前面有k-1个1，即：

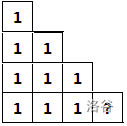
那么最后一位可填0或1，共2种方案。

总结一下，发现第一种和第二种可合并为$\sum\limits_{i=1}^{k-1}f(i)$,为了美观，我们设 $f(0)$ 为2，即可将第三种情况也合并，即：

$f(k)=\sum\limits_{i=0}^{k-1}f(i),f(0)=2$

• 当$k=1$时

$f(1)=f(0)=2=2^1$

• 当$k>1$时

因为$f(k-1)=\sum\limits_{i=0}^{k-2}f(i)$

所以$f(k)=\sum\limits_{i=0}^{k-1}f(i)=\sum\limits_{i=0}^{k-2}f(i)+f(k-1)=2*f(k-1)$

综上，$f(k)=2^k$

那么那么n个元素的方案总数即为$f(k)^n$即$2^{kn}$。

---

优化：

呐有人就要问了这不就是个快速幂板子题吗，有什么优化？对不起的确是有的。

由于我们取模的数1,000,000,007是个质数，所以有费马小定理：$a^{p-1}\equiv 1\pmod p$，也就是说我们可以对指数取模从而减少那么几次运算量，即$2^{kn\mod 1000000006}$

---

代码：

不就是个快速幂板子吗，就不放代码了。

---

题外话：

很睿智的作者看到 n ， k 的范围大，于是反手就把k*n对1,000,000,007取了个模。（100->40）

有人就要问了，这道绿题你写这么长给谁看啊？没错这篇题解就是我用来练$\LaTeX$的！