自动搬运

查看原文

来自洛谷，原作者为

	xiejinhao 人间总有一两风，填我十万八千梦

搬运于2025-08-24 22:16:45，当前版本为作者最后更新于2020-01-31 18:37:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P6033 [Ryoku 的探索] 题解

声明：转载本文或文中内容（包括图片）请注明出处，否则本人保留依法追究其责任的权力。

吐槽

为啥我觉得很简单但是很多人说很难？

其实出题人这一题没有出的太难，因为只需要找一个结论就好。

正文

既然上面已经提到是结论题了，那么结论是什么呢？

题目说到，这是一张 $n$ 点 $n$ 边的无向连通图，大家手画一下就可以知道这是一棵基环树（带一个简单环的“树”）。然后题目还提到了行走的方式，即：一条边的一个端点走过了就不走，否则优先走美观度大的边。

我们分析一下这句话，什么情况下一个端点会走过？就是走到环上了。画张图就明白了：

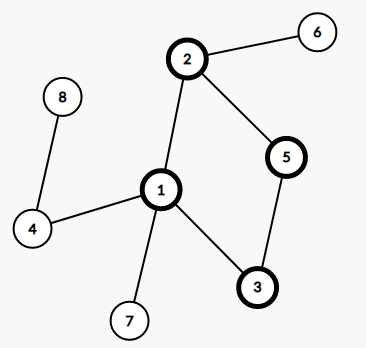
（一棵环为 $\{1,3,4,5\}$ 的基环树）

由上图可见，无论从哪个点进入环，环上总会有一条边不能经过（因为总会有一个端点被访问过），所以我们现在先考虑环上的点会忽略哪些边。

step1：对环上节点的处理

以上面那幅图为例，假设从 $2$ 进行深度优先遍历，这个时候有可能访问到节点 $6$，因为他不在环上是没有影响的（访问完 $6$ 及其相关子树又会回到 $2$），所以我们考虑继续遍历。接下来遍历到 $\{1,5\}$ 其中一者，假设遍历到 $5$，同理继续遍历 $3$、$1$，当遍历到 $1$ 时你会发现，$2$ 访问过了，因此可以确定 $\{2,5,3,1\}$ 在环上，在回溯的时候我们就以进行操作。

同时，你会发现如果我们从 $2$ 先遍历到 $5$，那么 $(1,2)$ 这条边就不会再次访问，简言之，对于环上节点 $i$ 及其相邻的两条环边（在环上的边） $e_1,e_2$，若按照美观度先访问了 $e_1$，（也就是 $p_1>p_2$），那么就会少走 $e_2$ 这条边，也就是少走了 $w_2$ 的长度。

因此对于环上的节点，我们可以把所有边的 $w$ 加起来，最后去判断要减去那一条环边即可。（刚刚已经提到，一个环上的节点恰好有两条环边）这样计算的复杂度就为 $O(1)$，加上找环，总的复杂度就为 $O(N)$。

如果你觉得比较懵，我们综合代码来理解：

if(vis[x]) { 
	一些内容;
	return true;
} vis[x] = 1;

上面这段代码的意思时：执行遍历的时候，我们用 $vis$ 记录每个点是否走过，如果走到了一个走过的节点，就意味着这个节点在环上，我们可以用一个 $vector$ 把整个环存下来。

刚刚提到了，存环需要回溯的时候实现，我们不妨把 $dfs$ 变为 $bool$ 的返回值类型，这样就更好判断。

先定义一些数组、变量：

int head[N], ver[M], Next[M], e[M], p[M];
// 边表

bool vis[N]; int End, Ep, Ee;
vector<int> ring;
long long ans[N];
// ans 答案   ring 存环用   vis 标记访问
// End 环的终止 Ep 终边的美观度 Ee 终边的长度
// 对于 End Ep Ee 下面还会解释

下面为整个找环过程的完整代码：

bool vis[N]; int End, Ep, Ee;
vector<int> ring;
long long ans[N];

bool dfs(int x, int fa, int fp, int fe) {
	if(vis[x]) { 
		End = x, Ep = fp, Ee = fe;
		return true;
	}
	vis[x] = 1;
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(y == fa) continue;
		if(dfs(y, x, p[i], e[i])) {
			if(x != End) 
				ans[x] -= fp > p[i] ? e[i] : fe;
			else  ans[x] -= p[i] > Ep ? Ee : e[i];
			ring.push_back(x);
			return x != End;
		}
	}
	return false;
}

请你观察回溯部分，如果回溯时这个点还在环上，即不是我们标记的环的 $End$（结尾，这个标记在第一个 $if$ 语句内），那么我们就可以一直往回标记，所以只要 $x ≠End$，说明环还没找完要一直返回真以便记录。

继续观察第一个 $if$ 语句以及回溯部分，你会发现，当你回溯的时候，除了标记的 $End$ 节点外，根据深度优先遍历的性质，一个节点的两条环边恰好连接了这个节点的父亲和儿子。因此除了 $End$ 节点，我们可以直接执行判断，对于一个点的环边，美观度小的边长需要从全集（即所有边长相加）中扣掉。

那么 $End$ 节点怎么解决呢？其实我们在第一个 $if$ 语句的时候恰好遍历了一条 $End$ 节点的环边，回溯过程又会遍历另一条，因此可以记录，然后按照上面的方法解决。

（还有不理解可以看代码或者私信我）

对于 $End$ 节点的执行深度优先遍历的时候可能有边不在环上的例子，可以看上图，从 $4$ 遍历，那么 $1$ 的父节点就为 $4$。

step2：对环外节点的处理

再次观察上面的结论，我们只解决了环上节点，那么环外节点呢？其实这就很简单了。比如对于节点 $4$，不论它先访问 $1$ 还是先访问 $8$，都要从 $1$ 进入环，其余非环上的边恰好都会经过一次，所以得出结论：对于环外节点，以环为根进行遍历，每个环上节点对应的子树内答案与该节点相等。

不信？不懂？那好，我们举个例子。假设从 $4$ 进行遍历，我们可以访问 $8$，然后回来访问 $1$，那么 $(1,4),(4,8)$ 均要经过；$1$ 可以先进行环的访问，这样必定会少经过一条边（就和从 $1$ 进入执行访问时一样的），然后回来再访问 $7$，$(1,7)$ 一定会经过；同理可知环外的边都一定会经过，那么 $8,4,7$ 作为起点的答案均与 $1$ 作为起点的答案相同。

那么就可以对环上节点一一遍历，将环看为根，给其子树一一赋值。

void dfs(int x) {
	vis[x] = 1;
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(vis[y]) continue;
		ans[y] = ans[x];
		dfs(y);
	}
}

以上就是赋值。赋值前把 $vis$ 清空并把环上节点全部标记为已访问即可。那么这一题也就解决了。

代码

（我知道你们只看这个）

（但是我的解释都在正文中，这是一份裸的代码）

#include<bits/stdc++.h>
#define reg register
using namespace std;

const int N = 1e6 + 10;
const int M = 2e6 + 10;

int head[N], ver[M], Next[M], e[M], p[M];

void add(reg int x, reg int y, reg int edge, reg int pi) {
	static int cnt = 0;
	ver[++cnt] = y, Next[cnt] = head[x], head[x] = cnt;
	e[cnt] = edge, p[cnt] = pi;
	
	ver[++cnt] = x, Next[cnt] = head[y], head[y] = cnt;
	e[cnt] = edge, p[cnt] = pi;
}

bool vis[N]; int End, Ep, Ee;
vector<int> ring;
long long ans[N];

bool dfs(reg int x, reg int fa, reg int fp, reg int fe) {
	if(vis[x]) { 
		End = x, Ep = fp, Ee = fe;
		return true;
	}
	vis[x] = 1;
	for(reg int i = head[x]; i; i = Next[i]) {
		reg int y = ver[i];
		if(y == fa) continue;
		if(dfs(y, x, p[i], e[i])) {
			if(x != End) 
				ans[x] -= fp > p[i] ? e[i] : fe;
			else  ans[x] -= p[i] > Ep ? Ee : e[i];
                        // 减去不会经过的边的答案
			ring.push_back(x);
			return x != End;
		}
	}
	return false;
}

void dfs(reg int x) { // 给子树赋值
	vis[x] = 1;
	for(reg int i = head[x]; i; i = Next[i]) {
		reg int y = ver[i];
		if(vis[y]) continue;
		ans[y] = ans[x];
		dfs(y);
	}
}

int read() {
	static char c;
	static int x;
	while(!isdigit(c = getchar()));
	x = c ^ 48;
	while(isdigit(c = getchar()))
		x = (x << 3) + (x << 1) + (c ^ 48);
	return x;
}

int main() {
	reg int n = read();
	reg long long sum = 0;
	for(reg int i = 1, x, y, e, p; i <= n; i++) {
		x = read(), y = read();
		e = read(), p = read();
		add(x, y, e, p);
		sum += e; // 把所有边权叠加
	}
	dfs(1, 0, 0, 0); memset(vis, 0, sizeof vis);
	for(reg int i = 0; i < (int)ring.size(); i++) 
		vis[ring[i]] = 1, ans[ring[i]] += sum;
       // 计算环上的答案
	for(reg int i = 0; i < (int)ring.size(); i++) 
		dfs(ring[i]);
	for(reg int i = 1; i <= n; i++)
		printf("%lld\n", ans[i]);
	return 0;
}

因为 $vector$ 常数比较大，输入文件也比较大，因此使用了寄存器和快速读入卡个常。

后记

感谢大家阅读了我的题解，同时也再次重申：若要转载，请注明出处。谢谢大家的观看和理解。

如果题解中有存在错误或者不理解的地方，请私信我（洛谷）。

（不知道可不可以无耻地要个赞）