自动搬运

查看原文

来自洛谷，原作者为

	WYXkk Zzz Zzz

搬运于2025-08-24 22:16:39，当前版本为作者最后更新于2020-01-24 23:56:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题解 轴对称

欢迎来到手算几何的世界

前置技能：基本几何变换（平移旋转轴对称）知识，相似三角形，推导手算几何的能力

引理 I：两次轴对称相当于一次平移或者旋转；反过来一次旋转或平移可以分解为两次平移或者旋转。

结合下图自行理解，严谨证明就略了其实我不会。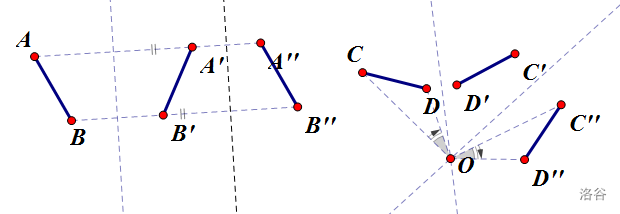

引理 II：一次旋转再一次平移相当于一次平移再一次旋转。

请再次结合下图理解，注意相似，严谨证明再次略去其实这个我会。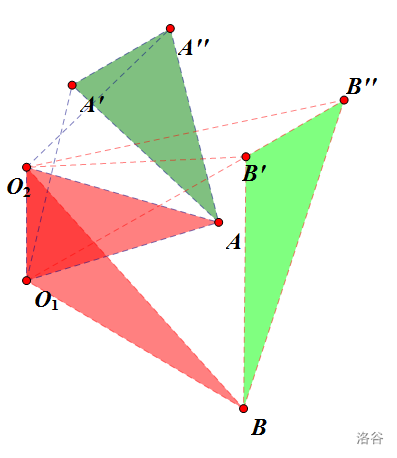

引理 III：本题的答案不超过 $3$。

证明：如果两个图形反向，那就把其中一个随便往哪里翻一下；然后将两个图形旋转至相同角度；最后平移至重合。后两次可以合并为一次旋转或平移，共计 $1+2=3$ 次轴对称就可以解决。

引理 IV：线段 $(x_1,y_1)$ $(x_2,y_2)$ 的垂直平分线是

$$2(x_1-x_2)x+2(y_1-y_2)y+(x_2^2+y_2^2-x_1^2-y_1^2)=0 $$

点 $(x,y)$ 关于直线 $Ax+By+C=0$ 对称的点的坐标为

$$(\frac{(B^2-A^2)x-2ABy-2AC}{A^2+B^2},\frac{(A^2-B^2)y-2ABx-2BC}{A^2+B^2}) $$

证明从略，手推即可。

于是，我们就有了下面的算法：

• 验证两个点集是否重合，如重合输出答案。
• 将任意一个不在对应点上的点翻折到对应点上。
• 重复上述过程。

可以证明这是对的。

$\texttt{code:}$

#include<cstdio>
#include<iostream>
#include<fstream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define Set(a) memset(a,0,sizeof(a))
#define F(i,a,b) for(register int i=a,i##end=b;i<=i##end;++i)
#define UF(i,a,b) for(register int i=a,i##end=b;i>=i##end;--i)
#define openf(a) freopen(#a".in","r",stdin);freopen(#a".out","w",stdout)
#define re register
#define ri re int
#define il inline
typedef long long ll;
typedef unsigned long long ull;
template<typename T> inline T rd(T& x)
{
	T f=1;x=0;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(T)(c-'0');
	x*=f;
	return x;
}
ll rd(){ll x;rd(x);return x;}
inline int max(int a,int b){return a>b?a:b;}
inline int min(int a,int b){return a<b?a:b;}
const int inf=1<<30;

typedef double db;
struct Point{db x,y;Point(db x=0,db y=0):x(x),y(y){}};//(x,y)
struct Line{db A,B,C;Line(db a=0,db b=0,db c=0):A(a),B(b),C(c){}};//Ax+By+C=0
Point dc(Point A,Line l)
{
	db x=l.A*l.A+l.B*l.B,y=l.A*l.A-l.B*l.B,z=2*l.A*l.B;
	return Point((-z*A.y-y*A.x-2*l.A*l.C)/x,(-z*A.x+y*A.y-2*l.B*l.C)/x);
}
Line small(Line l){while(fabs(l.A)>100000||fabs(l.B)>100000||fabs(l.C)>100000) l.A/=2,l.B/=2,l.C/=2;return l;}
Line mid(Point A,Point B){return small(Line(A.x-B.x,A.y-B.y,(B.x*B.x+B.y*B.y-A.x*A.x-A.y*A.y)/2));}
db eps=1e-2;bool eq(db a,db b){return fabs(a-b)<eps;}
bool eq(Point x,Point y){return eq(x.x,y.x)&&eq(x.y,y.y);}
Point A[20],B[20];Line ans[5];int num=0;int n;
void put(Line x){printf("%.6lf %.6lf %.6lf\n",x.A,x.B,x.C);}
void f(Line x){F(i,1,n) A[i]=dc(A[i],x);ans[++num]=x;}
void work()
{
    bool flg=true;F(i,1,n) flg=flg&&eq(A[i],B[i]);
    if(flg){printf("%d\n",num);F(i,1,num) put(ans[i]);exit(0);}
	for(int i=1,j=n;i<j;++i) while(eq(A[i],B[i])&&i<j){swap(A[i],A[j]);swap(B[i],B[j]);--j;}
	f(mid(A[1],B[1]));
}
int main()
{
	rd(n);
	F(i,1,n) scanf("%lf%lf",&A[i].x,&A[i].y);
	F(i,1,n) scanf("%lf%lf",&B[i].x,&B[i].y);
	while(true) work();
	return 0;
}