自动搬运

查看原文

来自洛谷，原作者为

	mRXxy0o0 风轻抚过琴弦，也吹乱一时思绪

搬运于2025-08-24 22:16:13，当前版本为作者最后更新于2023-09-27 21:45:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

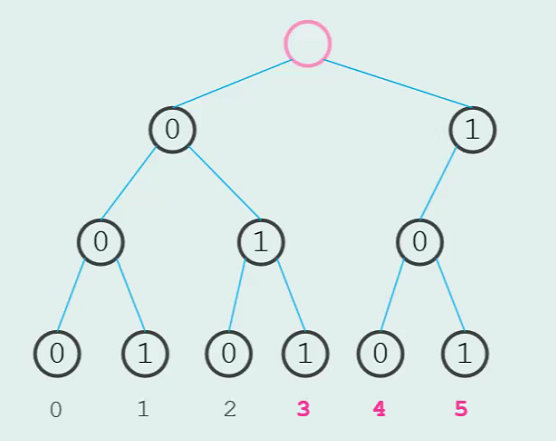
不妨在 Trie 树上考虑这个问题。

首先建一颗树：

这样一来，对于 $m$ 的限制就自然转化成了只取字典树的前半部分。

先考虑 DP，设 $f_{u,l,r}$ 表示 $u$ 号点的子树内取出 $b$ 数组中下标 $[l,r]$ 的部分。

我们考虑一个节点 $u$ 向其儿子转移的过程。很自然地，可以得到 $f_{u,l,r}=\max\limits_{k=l-1}^{r}(f_{ls,l,k}+f_{rs,k+1,r}+a_{k+1}+\dots+a_r)$ 的转移方程。

明显，这里无法枚举所有 Trie 树上的点。但是又发现，同一层上的点除了高位限制以外，本质上是一样的。

所以我们改进一下 DP 数组的定义。$f_{i,l,r,0/1}$ 表示第 $i$ 层之下取出 $b$ 数组中下标 $[l,r]$ 的部分，最后一维表示有无高位限制。按原式计算即可。

据说还可以四边形不等式优化，就看别的奆佬的题解吧（笑。

再仔细一想，发现它竟然和数位 DP 一模一样，其实这本质上是一致的。可是第一眼确实想不太到数位 DP。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=210,M=61;
int n,s[N][N];
ll f[M][N][N][2],a[N],m;
inline ll max(ll x,ll y){
	return x>y?x:y;
}
int main(){
	memset(f,-0x3f,sizeof f);
	scanf("%d%lld",&n,&m);
	for(int i=1;i<=n;++i){
		scanf("%lld",&a[i]);
		a[i]+=a[i-1];
		f[0][i][i][0]=f[0][i][i][1]=0;
	}
	for(int i=0;i<M;++i) for(int j=1;j<=n+1;++j) f[i][j][j-1][0]=f[i][j][j-1][1]=0;
	for(int i=1;i<M;++i)
		for(int l=1;l<=n;++l)
			for(int r=l;r<=n;++r){
				if(m&(1ll<<i-1)) for(int k=l-1;k<=r;++k) f[i][l][r][1]=max(f[i][l][r][1],f[i-1][l][k][0]+f[i-1][k+1][r][1]+a[r]-a[k]);
				else f[i][l][r][1]=f[i-1][l][r][1];
				for(int k=l-1;k<=r;++k) f[i][l][r][0]=max(f[i][l][r][0],f[i-1][l][k][0]+f[i-1][k+1][r][0]+a[r]-a[k]);
			}
	printf("%lld",f[M-1][1][n][1]);
	return 0;
}