【模板】差分约束

0
15011418730 LV 7 @ 2025-8-24 22:16:01
自动搬运

查看原文

来自洛谷，原作者为

Stephen_Curry
**

搬运于2025-08-24 22:16:00，当前版本为作者最后更新于2020-02-05 16:48:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解 P5960 【【模板】差分约束算法】

发布时间：2020.02.05
最近一次更新时间：2022.08.31

写在前面：本题解已经经过 $7$ 次审核，还请管理大大留情。
更新日志迁移到了这里

差分约束系统

如果一个不等式组由 $n$ 个变量和 $m$ 个约束条件组成，形成 $m$ 个形如 $x_j-x_i\leq k$ （ $i,j\in[1,n]$ 且 $k$ 为常数）的不等式，则称其为差分约束系统。换句话说，差分约束系统就是求解一组变量的不等式组的算法。

样例其实可以更为直观地写成以下不等式组：

$\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases} $

显然，这组不等式组的解是不唯一的，通过口算可以算出其中三组较小解：

$\begin{cases}x_1=5 \\ x_2=3\\x_3=5\end{cases}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{cases}x_1=0 \\ x_2=-2\\x_3=0\end{cases}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{cases}x_1=0 \\ x_2=0\\x_3=2\end{cases}$

问题转化

对于 $x_j-x_i\le k$ ，我们会发现它类似最短路网络中的三角不等式 $d_v-d_u\le w_{<u,v>}$ ，那是否可以通过最短路的形式解决呢？

显然是可以的，跑一遍最短路，此时最短路的答案 $d_i$ 也正是原不等式组的一个解 $x_i$ 。

此时，可将每个变量看成一个顶点，并设一个超级源点 $x_0$ ，它连向每个顶点（除了自身）且边权为 $0$ ，这时再对每一个不等式 $x_j-x_i\le k$ 连一条边权为 $k$ 的有向边 $<i,j>$ ，此时用 $x_j$ 表示超级源点到 $j$ 的最短路，用 $x_i$ 表示超级源点到 $i$ 的最短路，由于有边 $<i,j>$ 存在，从而有 $x_j\le x_i+k$ ，即为原不等式的变形。

在有解的情况下，最短路的答案 $d_i$ 就是原不等式组的一组解 $x_i$ 。

连边方法（2021.08.21 修改）

前文提到过，差分约束问题可以转化为最短路或最长路问题，所以两种转化也就形成了两种不同的连边方法。
1. 连边后求最短路
  将 $x_j-x_i\le k$ 变形为 $x_j\le x_i+k$ ，即从 $i$ 到 $j$ 连一条边权为 $k$ 的边。加入超级源点后求最短路，得到 $x_i\le 0$ 所有 $x$ 最大解。
2. 连边后求最长路
  将 $x_j-x_i\le k$ 变形为 $x_i\ge x_j-k$ ，即从 $j$ 到 $i$ 连一条边权为 $-k$ 的边。加入超级源点后求最长路，得到 $x_i\ge 0$ 所有 $x$ 最小解。
显而易见的，两种方法求出来的解大概率是不同的。样例中，用第一种方法得到的解为 $\begin{cases}x_1=0 \\ x_2=-2\\x_3=0\end{cases}$ ，而用第二种方法得到的解为 $\begin{cases}x_1=0 \\ x_2=0\\x_3=2\end{cases}$ 。

负环/正环判断

那么，如果万一用最短路求时出现负环，或用最长路时出现正环怎么办？

注：本段只考虑求最短路时的情况，最长路实质与最短路类似。

此时，咱们先不考虑怎么解决，先看这时的不等式组是什么样子的。

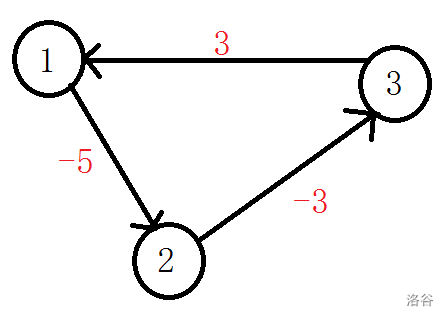
如上图，该图存在负环，如果一直沿着负环走，最短路径将会越来越小，最后到达 $-∞$ 。

而此时的不等式组为

$\begin{cases}x_1\le x_3+3 \\ x_2\le x_1-5\\x_3\le x_2-3\end{cases}$

经过替换，得 $x_1\le x_1-5$ ，这是不可能成立的。类似地，可以得出结论：若图中存在负环，则该不等式组无解。

此时，即可放心大胆地 SPFA，只需在 SPFA 的同时用一个数组来记录每个顶点入队次数，如果一个顶点入队次数大于 $n$ ，说明该图存在负环。（具体原因 StudyingFather 的题解里已经解释得很清楚了，这里就不再赘述了）

最长路问题（2021.08.21 修改）

题解里面普遍使用最短路求解，这里我来讲一下最长路的解法。

不过在说之前，这里还是要说一下区别于最短路的最长路问题。

最长路问题即为在给定的图中，计算从源点到所有顶点的最长路。保证图中没有正环。

其中一种实现方法为若 $d_u+w>d_v$ ，则将 $d_v$ 更新为 $d_u+w$ （实际上就是把最短路中的大于号改成小于号），并在初始化时将 $d$ 数组全部初始化为一个极小值，其余部分和用 SPFA 求最短路一样。

代码分解讲解

讲了这么多，这里便是重点了。

首先要实现 SPFA 求最长路，通过修改模板可以写出：
```
struct edge {
    int v, w, fail;
    //评论区有说不是 fail 是 tail 的……
    //确实，但变量名根据个人习惯有异是正常的，我一直到退役前都用的 fail.
    edge() {}
    edge(int _v, int _w, int _fail) {
        v = _v;
        w = _w;
        fail = _fail;
    }
} e[M << 1];
bool spfa(int u) {
    memset(vis, false, sizeof(vis));
    vis[u] = true;
    memset(dis, -1, sizeof(dis));  //因为是最长路，故要初始化为负数
    dis[u] = 0;
    memset(in, 0, sizeof in);
    in[u] = 1;
    queue<int> q;
    q.push(u);
    while (!q.empty()) {
        u = q.front();
        q.pop();
        vis[u] = false;
        for (int j = head[u]; ~j; j = e[j].fail) {
            int v = e[j].v;
            int w = e[j].w;
            if (dis[v] < dis[u] + w) { // 求最长路，和求最短路相反
                dis[v] = dis[u] + w;
                if (!vis[v]) {
                    q.push(v);
                    vis[v] = true;
                    ++in[v];
                    if (in[v] > n + 1) {  //判断负环，因为加了一个超级源点，故应跟 n + 1 而不是 n 比较。
                        return true;
                    }
                }
            }
        }
    }
    return false;
}
```
由于个人习惯，我比较倾向于将 head 数组初始化为 $-1$ ，于是便有了下面初始化函数：
```
void init() {
    memset(head, -1, sizeof(head));
    len = 0;
}
```
紧接着便是 add 函数，都是板子，不讲：
```
void add(int u, int v, int w) {
    e[len] = edge(v, w, head[u]);
    head[u] = len++;
}
```
最后就是主函数内容了，因为前文说了要对每一个不等式 $x_j-x_i\le k$ 从 $j$ 到 $i$ 连一条边权为 $-k$ 的边，从而调用 add 函数应为 add(u, v, -w)。

在不确定图是否完全联通的情况下，我们要添加一个超级源点 $x_0$ 与每个点都有一条权值为 $0$ 的边，前文已经说过。
```
for (int i = 1; i <= n; ++i) {
    add(0, i, 0);
}
```
最后看 SPFA 结果，若为真说明无解，输出 NO，否则依次输出 $dis_i$ 。

代码实现

无注释代码奉上。

以下为 $\text{2020.02.12}$ 更新的内容。

显然 SPFA 码量大还容易写炸 ~~（其实是自己太蒻老是写挂）~~，所以个人比较建议用 Bellman-Ford 算法来解决本题。

Bellman-Ford 算法描述（ $\text{2022.04.17}$ 修改）
1. 除源点外的所有顶点最短距离初始化为 $∞$ ，源点 $d_1$ 最短距离为 $0$ 。
2. 对边集 $E$ 进行 $n-1$ 次松弛操作。
3. 检查是否存在负权边，即是否存在未收敛的点。若存在，说明图存在负环，原不等式组无解；否则 $d_i$ 即为 $x_i$ 的一个解。
描述解释

相信像窝一样的蒟蒻们看到上面的算法描述肯定一头雾水，下面就来解释一下。

$Q_1$ ：为什么进行 $n-1$ 次松弛操作？
$A_1$ ：因为图的最短路径不包含负环或正环，故显然最多只能包含 $n-1$ 条边。

$Q_2$ ：何谓松弛操作？
$A_2$ ：一次松弛操作即描述点 $s$ 到点 $v$ 的最短路权值上界，反复进行松弛操作可求出两点最短路。举个例子，若要松弛 $\left(u,v\right)$ 一边，即是取 $s\to v$ 的最短路与 $s\to u\to v$ 的最短路的最小值。

$Q_3$ ：何谓“未收敛”？
$A_3$ ：未收敛即为仍能松弛，此时路径仍非最短。若经过 $n-1$ 轮松弛操作后仍能松弛，说明图存在负权回路。

代码分解详解

显然首先我们要建立一个结构体记录每条边的起点 $u$ ，终点 $v$ 与权值 $w$ ，不妨将此数组命名为 $e$ 。
```
struct edge { 
    int u, v, w; 
} e[5050];
```
读入部分唯一要注意建边要建反向边，不难得出以下代码：
```
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {  //这里不能写成while(m--)，因为m在后面还要使用
    scanf("%d%d%d", &c, &c1, &y);
    e[i].u = c1, e[i].v = c, e[i].w = y; //反向边
}
//初始化因为太简单直接省略，不会的可以看后面的全代码
```
紧接着是 Bellman-ford 算法核心部分。首先第一重循环控制松弛操作的次数：
```
for (int i = 1; i < n/*等价于 <= n-1，因为共 n-1 次松弛操作*/; i++) {

}
```
第二重循环控制松弛的边，即对哪一条边进行松弛操作；循环内即是更新 $d_{e_i.v}$ 的值。
```
// Bellman-Ford 核心代码 
for (int i = 1; i < n; ++i) {
    for (int j = 1; j <= m; ++j) { //共 m 条边
        //d[i] 表示从 1 到 i 的最短路
        d[e[j].v] = min(d[e[j].u] + e[j].w, d[e[j].v]);
    }
}
```
最后判断是否存在未收敛的点，代码与核心代码判断是否松弛的代码仅仅是把 $j$ 改成了 $i$ 而已。
```
for (int i = 1; i <= m; ++i) 
	if (d[e[i].v] > d[e[i].u] + e[i].w)  //仍能松弛
	    return !printf("NO");  //直接结束程序
```
否则依次输出 $d_1,d_2,\dots,d_n$ 即可。

完整代码也还在这个剪贴板里，往下翻。

标准二十行代码，当前最短解 ~~（预感不保）~~ （2021.08.21 更新：早就被超了）。

算法对比（2021.08.21 修改）

现在来对比一下两种算法。

显然 SPFA 虽然代码长，但速度明显更快；Bellman-Ford 代码短，速度较慢。

顺带提一句，SPFA 最坏情况下与朴素 Bellman-Ford 相同，为 $O(VE)$ ，碰到部分凉心出题人时请慎用。

以下为 $\text{2020.02.13}$ 更新的内容。

关于算法问题暂时先讲到这里。如果还有不懂的话欢迎评论区询问我。

这里是想到关于差分约束有一些推论与定理，想在这里说一说。

（部分内容借鉴算法导论）

对于每个 $x_j$ 和 $x_i$ ，显然有 $x_j-x_i=(x_j+d)-(x_i+d)$ 。

从而若向量 $x$ 满足 $A_x\leq b$ ，则向量 $x+d$ 同样满足该条件。

听不懂？我们就拿样例来说吧。

样例给的输出是 $\begin{cases}x_1=5 \\ x_2=3\\x_3=5\end{cases}$ ，那么将 $x_1,x_2,x_3$ 同时加上或减去任意一数，它必然也满足条件。

从而，我们得出了推论 1：设向量 $x=(x1,x2,\cdots,x_n)$ 为差分约束系统 $A_x\leq b$ 的一个解，设 $d$ 为任意常数，则 $x+d=(x_1+d,x_2+d,\cdots,x_n+d)$ 也是该差分约束系统的一个解。

由该推论，我们可以把或许求出的很怪异的不等式解变成正整数解，看起来更自然。

推论 2：给定差分约束系统 $A_x\leq b$ ，设 $G=(V,E)$ 是该差分约束系统所对应的约束图，若图 $G$ 不包含负环，则
$$x=(\delta(v_0,v_1),\delta(v_0,v_2),\delta(v_0,v_3),\dots,\delta(v_0,v_n)) $$
是该系统的一个可行解。

证明：

考虑任意一条边 $(v_i,v_j)\in E$ ，根据三角不等式， $\delta(v_0,v_j)\le\delta(v_0,v_i)+w(v_i,v_j)$ ，从而 $x_j-x_i=\delta(v_0,v_j)-\delta(v_0,v_i)\le w(v_i,v_j)$，命题得证。

由该推论，我们可以自然而然的想到 SPFA 和 Bellman-Ford 这两种算法了。

算法引申

当然，很多类似差分约束的问题都不会像这题一样良（du）心（liu），它们很可能不会只局限于形如 $x_j-x_i\le k$ ，有可能会有 $x_j-x_i\ge k$ 或 $x_j-x_i=k$ 之类的式子存在。

其实只需改动建边方法即可解决。 $x_j-x_i\ge k$ 的情况很简单，相信大家稍加思考就可以想通。而 $x_j-x_i=k$ 时，只需将它拆成 $x_j-x_i\le k$ 和 $x_j-x_i\ge k$ 两种情况建两条边即可。

算法优化

关于两种算法的优化其实有很多，这里随便举出几种。
1. SPFA 可以通过 SLF 或 LLL 优化策略进行优化；
2. 此处举出的 Bellman-Ford 算法没有加入超级源点，所以跑出来的结果是 $0,\inf,\inf+2$ ，不好看。可以考虑加入超级源点。
参考资料

《算法导论》

~~百度百科~~（ $\text{2022.04.17}$ 修改：已经替换下所有百度百科的内容）。

以上便是本题解的全部内容。

写了这么多，希望这篇题解能帮助到您。

由于篇幅过长，当中难免有纰漏之处，如您有发现请私信本蒟蒻，有空一定会去修的。

完。