自动搬运

查看原文

来自洛谷，原作者为

	maruize :)

搬运于2025-08-24 22:16:00，当前版本为作者最后更新于2020-02-22 14:45:55，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

少有的构造题

我们可以想象这样一个形状：

(一条线上挂一堆点)

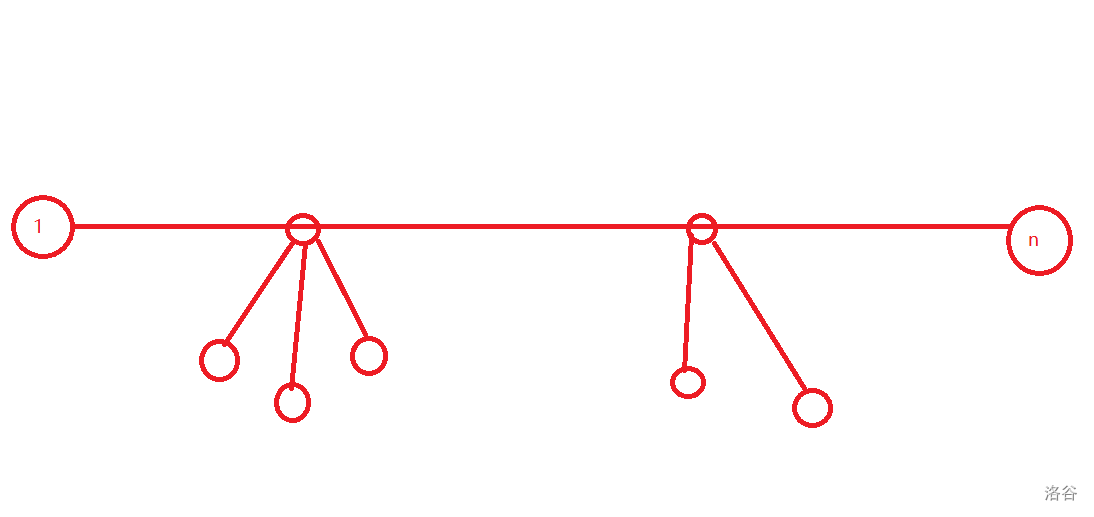
(图画的不好)

首先考虑在线上的点

要想知道哪些点在线上，只要知道1-n的距离

显然他是

因为如果d(1,n)比这个长的话$d(1,i)+d(i,n)<d(1,n)$的点将无处安放。

然后考虑剩下的点能不能挂上

$M=d(t,i),X=d(1,t),Y=d(t,n)$

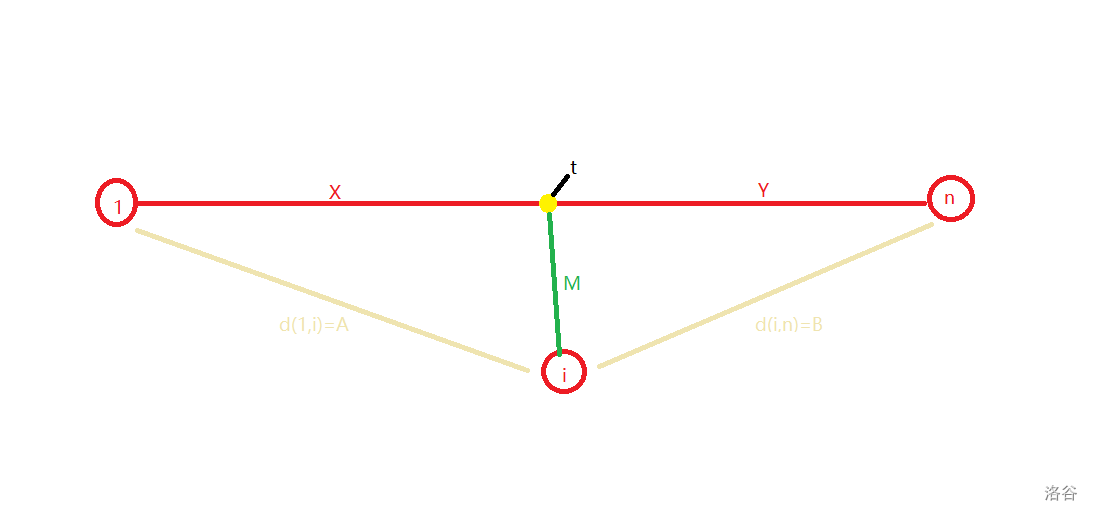
如图，若点i能挂在位置为t的点，则

$A=X+M(1),B=Y+M(2)$

$(1)-(2)$得$A-B=X-Y$。

所以判断一个点i是否能挂在线上，只要判断是否有在线上的点j使

$d(1,i)-d(i,n)=d(1,j)-d(j,n)$。

开个桶存一下即可。

code：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
int n;
void WA(){puts("NIE"),exit(0);}
struct data{int x,y,id;}f[500005];
bool cmp(data a,data b)
	{return a.x+a.y==b.x+b.y?a.x<b.x:a.x+a.y<b.x+b.y;}
bool CMP(data a,data b){return a.x<b.x;}
int ope[10000005],*val=ope+5000000;//桶
//要开够，要不RE|WA|UKE。。。
int fa[500005],v[500005];
signed main(){
	int M=0x3f3f3f3f;
	scanf("%d",&n);//cout<<n<<endl;
	for(int i=1;i<=n;i++)f[i].id=i;
	for(int i=2;i<n;i++)scanf("%d",&f[i].x);
	for(int i=2;i<n;i++)scanf("%d",&f[i].y);
	for(int i=2;i<n;i++)M=min(M,f[i].x+f[i].y);
	f[1]={0,M,1},f[n]={M,0,n};
	
	sort(f+1,f+n+1,cmp);//排序来分隔在线上的和不在的。
	int s;
	val[-M]=1;//往桶里塞进d(1,1)-d(1,n)
	for(s=2;s<=n;s++){
		if(f[s].x+f[s].y==M){//在线上
			if(f[s].x==f[s-1].x)WA();//点间距离!=0
			val[f[s].x-f[s].y]=s;
            //往桶里塞进d(1,s)-d(s,n)
		}
		else break;//不在
	}
	for(int i=s;i<=n;i++){
		int&t=val[f[i].x-f[i].y];
		if(t)fa[i]=t,v[i]=f[i].x-f[t].x;
		else WA();
	}
	puts("TAK");
	for(int i=2;i<s;i++)
		printf("%d %d %d\n",f[i-1].id,f[i].id,f[i].x-f[i-1].x);
	for(int i=s;i<=n;i++)
		printf("%d %d %d\n",f[fa[i]].id,f[i].id,v[i]);
	return 0;
} 

结束？

然后你光荣的得了80pts。

这是漏了一种情况：

1-n的路径上没有其他点

like this：

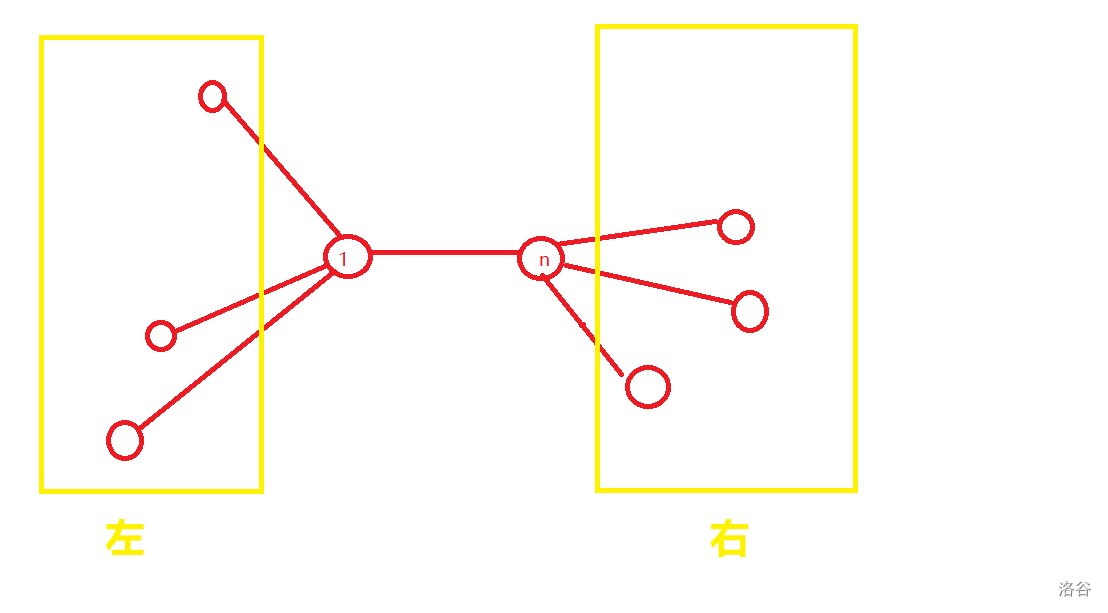
这时d(1,n)就不是原来的了。

d(1,n)=

$\$d(1,i)-d(i,n)$\$[ i在“左侧” ]

$\$d(i,n)-d(1,i)$\$[ i在“右侧” ]

只有对于所有的i，d(1,n)相等才可以。

所以特判一下：

bool flag=1;
for(int i=3;i<n;i++)if(abs(f[i].x-f[i].y)!=abs(f[2].x-f[2].y))flag=0;
if(!flag)return;
int M=abs(f[2].x-f[2].y);//M=d(1,n)
if(M==0)return;
puts("TAK");
printf("1 %d %d\n",n,M); 
for(int i=2;i<n;i++){
	//if(f[i].x==f[i].y)return;
	if(f[i].x<f[i].y)printf("1 %d %d\n",i,f[i].x);
	else printf("%d %d %d\n",i,n,f[i].y);
}exit(0);