1 条题解
-
0
自动搬运
来自洛谷,原作者为

wsyhb
**搬运于
2025-08-24 22:15:44,当前版本为作者最后更新于2022-02-09 12:15:28,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题解
首先,如果你画几个多边形来手玩,你会发现如下结论:
结论一:对于凸多边形中的任意一个三角形及它的任意一边,要让这个三角形的这条边成为操作后多边形的某边,必须删除这个三角形这一侧的其它所有三角形。
文字可能不是那么容易理解,下面举例说明:
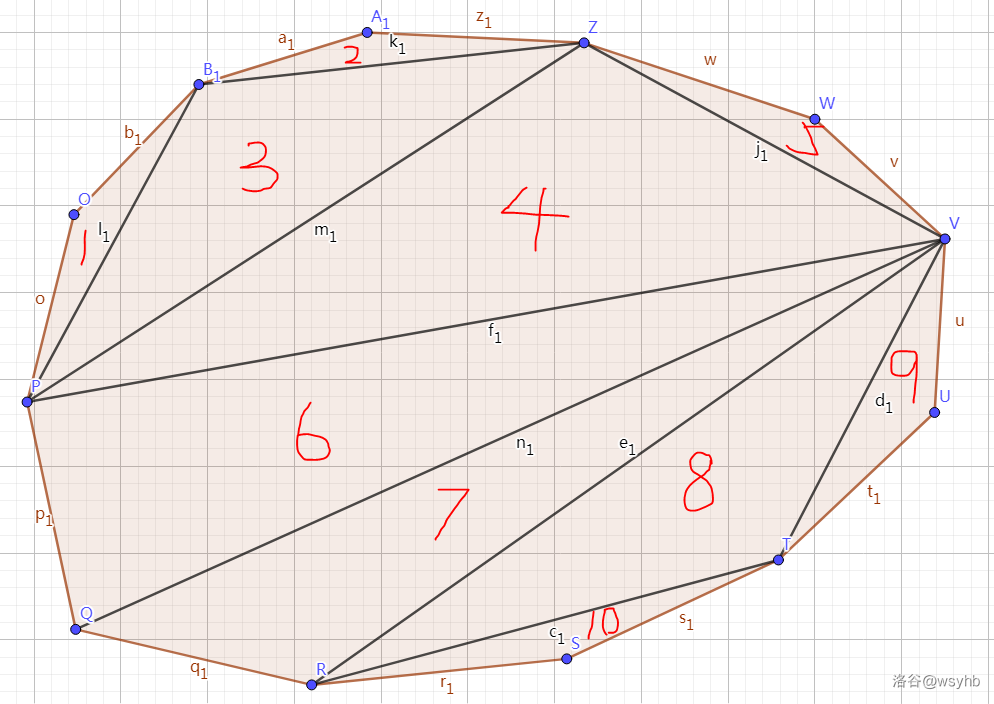
如上图,这个 边形包含 个三角形,其中的红色数字表示它们的编号。
用 表示第 个三角形,那么要让 的 这条边成为操作后多边形的某边,必须删除 和 ;要让 的 这条边成为操作后多边形的某边,必须删除 和 ;要让 的 这条边成为操作后多边形的某边,必须删除 。
是不是感觉这个结论很显然?不过还是要给出证明的:
设多边形边数为 ,容易验证 时结论一成立。
假设 时结论一成立,下证 时结论一仍然成立。对于有两边都是整个多边形的边的三角形,结论一显然成立。
对于有至少两边都不是整个多边形的边的三角形 ,设它的三边分别为 ,且 都不是整个多边形的边。
(换句话说, 这两侧都有其它三角形)
那么要使 成为操作后多边形的某边,必须删除以 为边的另一个三角形 。考虑如何在删除三角形 的同时不删除三角形 :这相当于不能完全删除 的 边另一侧(即包含三角形 的这一侧),于是包含三角形 的这一侧的部分可以被等效替换为一个单独的三角形 ,而 不能被删除。
等价替换后总的三角形个数变少了,于是多边形的边数也由 降到了 。
根据归纳,要删除 (即让 除 以外的两边成为多边形的边),必须删掉除 以外的所有三角形。
即结论一对于 的边 成立。
同理可证 的边 成立。根据归纳,结论一对任意多边形的任意三角形的任意边成立。
回到原题,设黑色三角形每一侧的三角形个数分别为 ,那么问题转化为:
- 给定三堆石子,数量依次为 。
- 两人轮流操作,每次选取一堆石子并从其中取走一颗。
- 当三堆石子中有至少两堆石子为空时,游戏结束。
- 进行最后一次操作的人失败。
说明:当黑色三角形有至少两边为多边形的边时,当前玩家把黑色三角形删除即可取得游戏的胜利。故造成这种局面的玩家失败。
我想到这儿的第一反应:直觉上,局面的胜负与 的奇偶性有关。(因为每次只取一颗石子)
但我并不是很确定具体结论,于是写了个程序打了下 的胜负状态:
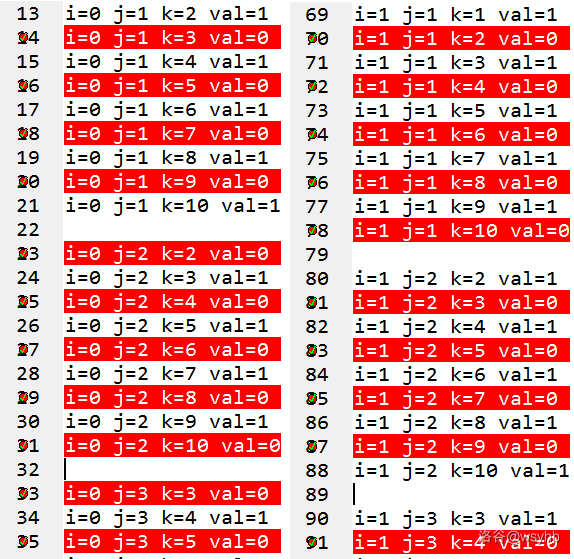
(其中 表示该局面必败, 表示必胜;程序见剪贴板)
这规律简直不要太明显:当 为偶数时必败,反之必胜。
更严谨地,我们有如下结论:
结论二:
- 当 中有至少 个 时,该局面必胜。
- 否则,该局面必胜当且仅当 为奇数。
证明:
1 显然,故接下来考虑 中有至多 个 的情况。
由于必存在某一时刻某堆石子被取空(或一开始就没有),故可以考虑只剩两堆石子 的情况。除非万不得已,玩家一定不会把这两堆石子中的某一堆取空。
即:除非 ,玩家一定不会把 中的任意一个变为 。
这意味着最终的局面一定是 (要操作该局面的玩家获得胜利)。
即:最终,不为空的这堆石子个数为 。而每次操作都会改变 的奇偶性,故 为奇数的局面必胜。
如何求 呢?
设黑色三角形三点编号为 ,则 为三点编号均在 中的三角形个数, 为三点编号均在 中的三角形个数,剩余三角形的个数即为 。
( 的顺序显然不影响答案)于是这道题就做完了。
过程比较简单,但却写了一大堆,好累啊。代码
#include<bits/stdc++.h> using namespace std; int main() { int n,a,b,c; scanf("%d%d%d%d",&n,&a,&b,&c); if(a>b) swap(a,b); if(a>c) swap(a,c); if(b>c) swap(b,c); int x=0,y=0,z=0; for(int i=1;i<=n-3;++i) { int p,q,r; scanf("%d%d%d",&p,&q,&r); if(p>=a&&p<=b&&q>=a&&q<=b&&r>=a&&r<=b) ++x; else if(p>=b&&p<=c&&q>=b&&q<=c&&r>=b&&r<=c) ++y; else ++z; } int cnt0=(x==0)+(y==0)+(z==0); if(cnt0>=2) puts("TAK"); else if((x+y+z)&1) puts("TAK"); else puts("NIE"); return 0; }
- 1
信息
- ID
- 4950
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
