自动搬运

查看原文

来自洛谷，原作者为

	yangrunze 蓝蓝的天空银河里，有只小白船

搬运于2025-08-24 22:15:44，当前版本为作者最后更新于2020-07-17 22:07:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这计算量……可真是……酸爽……

（正因为如此，接下来的内容中，我会尽量完整地展现计算过程，如果你是懒癌晚期不想亲自算的话，计算的部分可以直接跳过）

---

咳咳，这个题，我的思路是这样的：设小人走过离灯泡的距离为 $x$ ，求出影长 $y$ 与 $x$ 的函数解析式，这样不就转化成求函数最值的问题了嘛~

那怎么求呢？我们利用几何知识——相似三角形。

当然，这个题有一个小地方需要注意——对于不同的位置，我们要分类讨论（经历过数学中考的我已经轻车熟路~）

（以下图片都由万能的 desmos 赞助播出~动态图戳这体验）

（P.S. ：以下图片中，$AB$ 是灯泡，$MN$ 是小人）

1. 当影子全部落在地面上时：

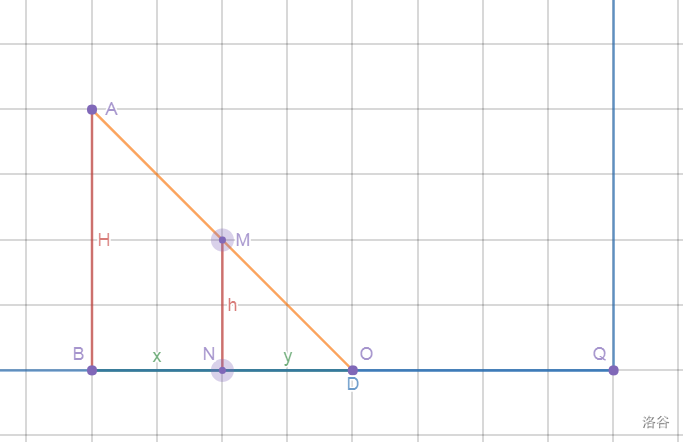
根据初三的几何知识，我们可以轻松得到 $\triangle OAB \sim \triangle OMN$

进而可以得到 $\dfrac{AB}{MN}=\dfrac{OB}{ON}$

再根据我们前面函数的定义，可以得到 $\dfrac{H}{h}=\dfrac{x+y}{y}$

把比例式交叉相乘化成等积式，$h(x+y)=Hy$

去括号，移项，合并同类项，得 $hx+hy=Hy,(H-h)y=hx$

即 $y=\dfrac{h}{H-h}x$

当然，别忘了考虑自变量的取值范围：要保证影子完全落在地面上，我们还有一个要求就是 $x+y\le D$，

即 $\dfrac{h}{H-h}x+x\le D$

通分合并同类项，可以解得$\dfrac{H}{H-h}x\le D$，

$x\le D\dfrac{H-h}{H}$

所以第一种情况的函数解析式为 ：$y=\dfrac{h}{H-h} x\quad(0\le x\le D\dfrac{H-h}{H})$

2. 当影子有一部分落在墙上时：

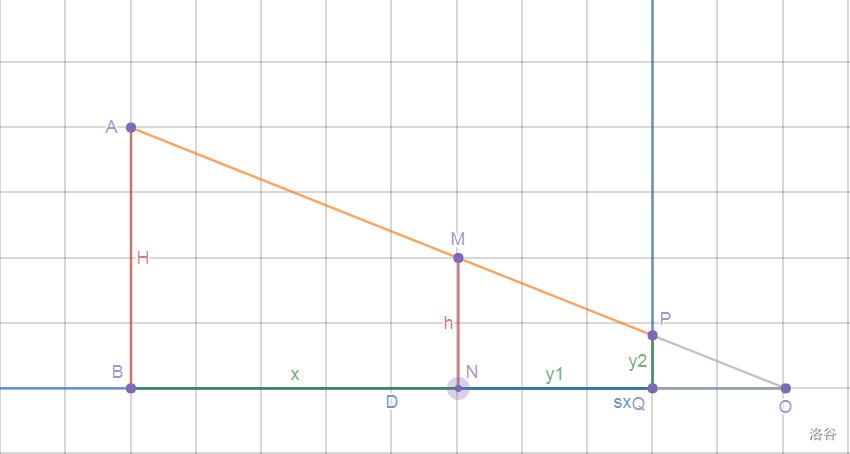
这时，影长被分为了两部分：我们设 $QN=y_1,PQ=y_2$

肉眼可见 $y_1=D-x$，那我们只要求出 $y_2$ 就可以啦！

那 $y_2$ 怎么求呢？我们注意到，上一种情况的那组相似三角形依然存在，延长 $BN,AM$ 交于点 $O$，还是 $\triangle OAB \sim \triangle OMN$

这样的话，根据上一种情况可得 $ON=\dfrac{h}{H-h}x$

为了方便后续计算，设 $\dfrac{h}{H-h}=s$，$ON=sx$。

我们发现，还有一组相似三角形：$\triangle OPQ \sim \triangle OMN$

即： $\dfrac{MN}{PQ}=\dfrac{ON}{OQ}$

把我们刚才设好的东西都代进去：$\dfrac{h}{y_2}=\dfrac{sx}{sx-y_1}$

将 $y_1=D-x$ 代入：$\dfrac{h}{y_2}=\dfrac{sx}{sx-D+x},\dfrac{h}{y_2}=\dfrac{sx}{(s+1)x-D}$

即：$sx\times y_2=h[(s+1)x-D]$

将$sx$除过去，可以得到$y2=\dfrac{h[(s+1)x-D]}{sx}$

当然，我们还可以继续化简：我们注意到分子分母都有相同的 $x$，可以拆出来约掉：

$\begin{aligned}y2=h\times[\dfrac{(s+1)x- D}{sx}]\\=h\times[\dfrac{(s+1)x}{sx}-\dfrac{D}{sx}]\\=h\times(\dfrac{s+1}{s}-\dfrac{D}{sx})\end{aligned}$

将 $s=\dfrac{h}{H-h}$ 代回到式子里面：

$\begin{aligned}y2=h\times(\dfrac{s+1}{s}-\dfrac{D}{sx})\\=h\times(\dfrac{\dfrac{h}{H-h}+1}{\dfrac{h}{H-h}}-\dfrac{D}{\dfrac{h}{H-h}x})\\=h\times(\dfrac{\dfrac{H}{H-h}}{\dfrac{h}{H-h}}-\dfrac{D}{\dfrac{h}{H-h}x})\\=h\times(\dfrac{H}{h}-\dfrac{D(H-h)}{hx})\end{aligned}$

将 $h$ 乘进去：$y_2=H-\dfrac{D(H-h)}{x}$

然后根据 $y=y_1+y_2$，再加上自变量取值范围，这一段的函数也就出现了：

$y_=D-x+H-\dfrac{D(H-h)}{x}(\dfrac{H-h}{H}\le x\le D)$

这样的话，这个函数就很清晰得展现在我们眼前了：

$y=\begin{cases}\dfrac{h}{H-h} x\quad(0\le x\le D\dfrac{H-h}{H})\\D-x+H-\dfrac{D(H-h)}{x}(D\dfrac{H-h}{H}\le x\le D)\end{cases}$

（动态图戳这）

---

接下来，我们来考虑这个函数的最大值：这个函数时由两部分组成的，我们只需要把两部分的最大值都求出来，再取个 $\max$ 就行了。

第一个函数非常简单：它是个斜率大于 $0$ 的正比例函数，最大值就是当 $x=D\dfrac{H-h}{H}$的时候，算出 $y_{\max}=\dfrac{h}{H-h}\times D\dfrac{H-h}{H}=\dfrac{Dh}{H}$

那至于第 $2$ 个函数呢，我们先把它变一下：

$y=D+H-[\color{red}{x+\dfrac{D(H-h)}{x}}\color{black}]$

有没有发现红色的部分有点眼熟呢？？？

熟读高中数学必修一的小伙伴们肯定都看出来了：这是对钩函数！

（科普：对钩函数就是形如 $y=ax+\frac{b}{x}$的函数，是由一次函数和反比例函数相加而成，由于图像像两个，因此而得名）

我们都知道，对钩函数是跟基本不等式密不可分的。

基本不等式是啥？ 当 $a>0,b>0$时，$a+b\ge 2\sqrt{ab}$

这有什么关系？我们把这部分对勾函数带到基本不等式里看看：

$x+\dfrac{D(H-h)}{x}\ge 2\sqrt{x\times\dfrac{D(H-h)}{x}}$

即 $x+\dfrac{D(H-h)}{x}\ge 2\sqrt{D(H-h)}$

这一部分的最小值出来啦！

也就是说，这个函数的最大值就是$D+H-2\sqrt{D(H-h)}$

$\cdots\cdots$

吗？

肯定没那么简单！在本题中，自变量是有取值范围的，也就是说：这是一个区间最值问题，我们要判断当 $y$ 是这个“最大值”的时候， $x$ 到底能不能取到。

那怎么判断能否取到呢？别忘了，在基本不等式中有一句话是特别重要的：

当且仅当 $a=b$ 时，等号成立。

也就是说，当 $y$ 取到最大值 $D+H-2\sqrt{D(H-h)}$ 时，$x=\dfrac{D(H-h)}{x}$

去分母，得到 $x^2=D(H-h)$

解得 $x_1=\sqrt{D(H-h)},x_2=-\sqrt{D(H-h)}$（舍去）

也就是说，当且仅当 $x=\sqrt{D(H-h)}$ 时，$y$ 取到最大值。

不仅如此，我们还可以发现：当 $x<\sqrt{D(H-h)}$ 时，$y$ 随 $x$ 的增大而增大；当 $x>\sqrt{D(H-h)}$ 时，$y$ 随 $x$ 的增大而减小。（对钩函数的性质，有兴趣的小伙伴们可以证明一下）

就这样，我们就可以画出函数的大致图像。最后一步，就是结合图像分析在各个区间内的最值啦！

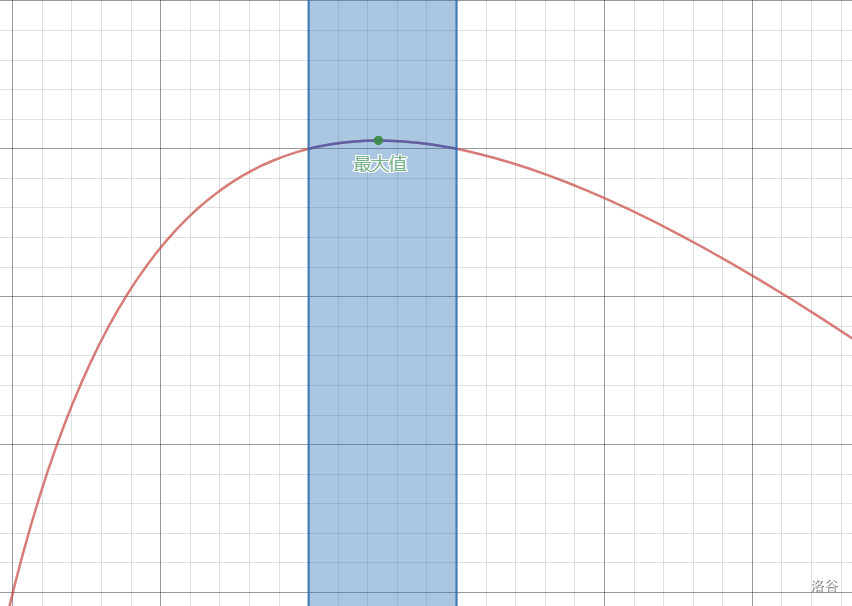
首先，当 $D\dfrac{H-h}{H}\le \sqrt{D(H-h)}\le D$ 时，没说的，最大值就是 $D+H-2\sqrt{D(H-h)}$S

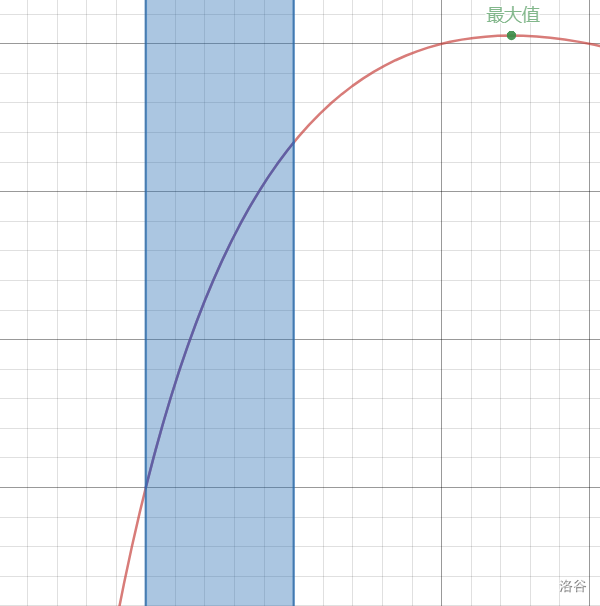
其次，当 $\sqrt{D(H-h)}\ge D$ ，也就是取值范围在最大值的左边时，这时函数单调递增，当$x=D$ 时，$y=D-D+H-(H-h)=h$

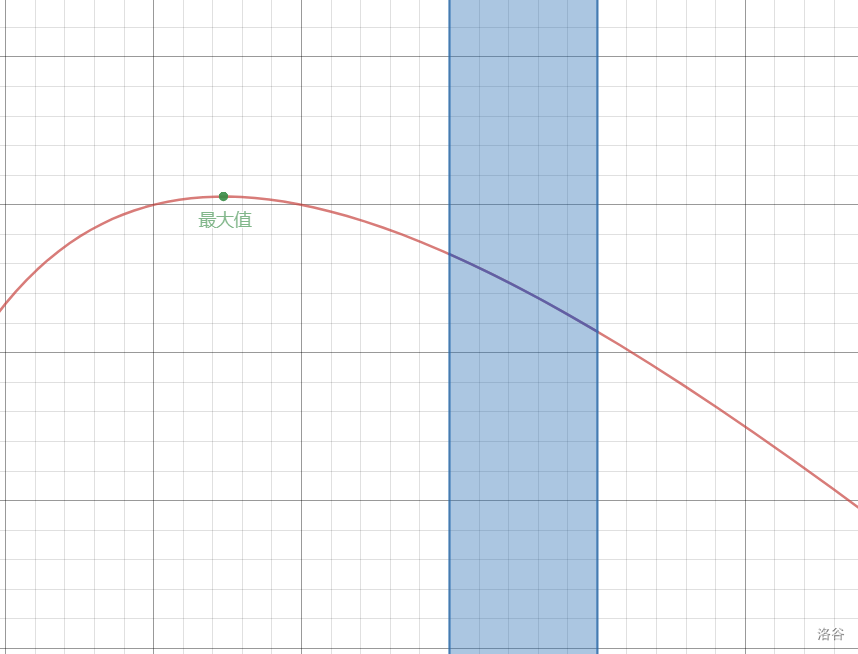
最后，当 $\sqrt{D(H-h)}\le D\dfrac{H-h}{H}$ ，也就是取值范围在最大值的右边时，这时函数单调递减，当$x=\dfrac{H-h}{H}$ 时，$y=D-(H-h)\times\dfrac{D}{H}$

All in all, 第二部分的函数的最大值是这样的：

$y_{\max}=\begin{cases}D-(H-h)\times\dfrac{D}{H}\quad (\sqrt{D(H-h)}\le D\dfrac{H-h}{H})\\D+H-2\sqrt{D(H-h)}\quad(D\dfrac{H-h}{H}\le \sqrt{D(H-h)}\le D)\\h\quad(\sqrt{D(H-h)}\ge D)\end{cases}$

这样的话，我们就成功求出了函数的最大值！

（代码很好写，我就不贴了）

---

方法讲完了，不过这时肯定还有小朋友有疑问：

——“yrz，我不会基本不等式和对钩函数，那怎么办呀？”

别急，我们还有一种方法——三分法。

虽然不会对钩函数，但经过适量分析，也可以发现第二部分的函数先递增，后递减，是一个单峰函数。

三分和我们熟悉的二分类似，都是每次把答案锁定在一个区间，大事化小，小事化了。我们都知道，二分是很适合单调函数的（就是要么一直上升，要么一直下降，不拐弯）；而三分呢，它适用于单峰函数或单谷函数（就是“只拐一次弯”，会出现一个最小值/最大值）

不仅如此，三分的代码和二分也很像，就是把当前的区间平均分成 3 份，然后根据两个分界点（相当于二分的 mid）的函数值确定答案在这三个区间的某一个里面。具体的操作我就不细说啦，想学的小伙伴们可以去看其它题解或者找模板题玩玩~

---

$\huge \color{springgreen}The\;end$

$\tiny\text{(P.S:中考终于考完了)}$