自动搬运

查看原文

来自洛谷，原作者为

	Larryyu Euphoric NocturNe |AS| ALTERing EGO

搬运于2025-08-24 22:15:42，当前版本为作者最后更新于2024-08-23 09:29:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

给定 $n$ 个半平面 $a_i x+b_i y\le c_i$ 和 $p$ 个关键点 $(x_i,y_i)$，第 $i$ 个半平面有价格 $w_i$，你需要选择一些半平面覆盖所有的关键点，同时使总价格最小。

求最小的总价格。

Solution

此解法为 $O(n^4)$ 正解，并非随机化算法，同时码量小，最优解前三。

同时不需要对半平面做任何操作，也不需要对关键点做分类，或作出一个新的坐标系。

在纸上画一些半平面后容易发现，半平面未覆盖的区域为一个凸包或凸壳，由于凸包和凸壳没有本质区别，为方便表述，下文以凸包为例。

同时我们还发现，最优情况下所有半平面都限制凸包，如图。

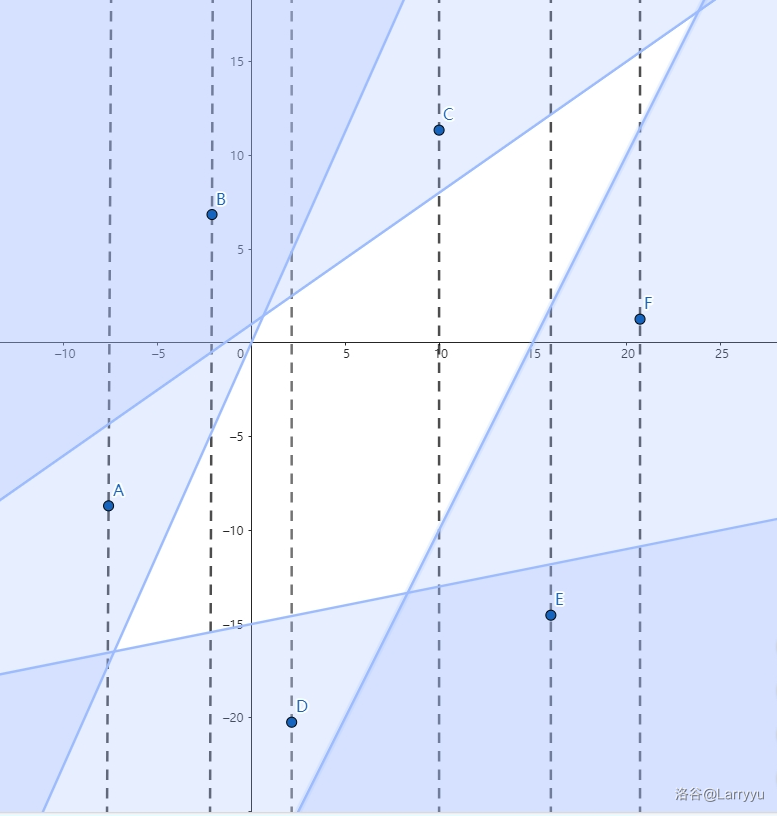
因为一个半平面若不限制凸包可以直接不选，减少花费。

用一条平行于 $y$ 轴的线从左到右去扫描凸包，发现不论横坐标为何值都只有两个半平面在限制凸包。

对于关键点而言，只要此时限制凸包的两个半平面能覆盖它就是合法的，否则要再添加一个半平面来覆盖它。

容易想到用动态规划来进行此操作。

设 $dp_{i,j,k}$ 表示当前扫描线已移动到第 $i$ 个关键点（关键点已按横坐标排好序），上下限制凸包的半平面标号为 $j,k$（钦定 $j<k$），此时的最小花费。

初始化将 $dp$ 全设为 $\inf$。

边界为 $dp_{0,j,k}=w_j+w_k(0\le j<k\le n)$。

设 $check(i,j)$ 表示第 $i$ 个点是否被第 $j$ 个半平面覆盖。

依照上文操作得出转移方程：

$\begin{cases}dp_{i,j,k}=\min(dp_{i,j,k},dp_{i-1,j,k})&check(i,j)\lor check(i,k)=true\\dp_{i,j,l}=\min(dp_{i,j,l},dp_{i-1,j,k}+w_l)&check(i,l)=true\\dp_{i,k,l}=\min(dp_{i,k,l},dp_{i-1,j,k}+w_l)&check(i,l)=true\end{cases}$

那么答案就为 $\min\limits_{0\le j<k\le n}dp_{p,j,k}$。

为什么此方程不会选择同一个半平面多次呢？

因为若 $l$ 在 $j,k$ 前已选择且为最优方案，那么在后来的任意横坐标下，$j,k$ 覆盖的范围严格优于 $l$，取最小值时会被除去，因此不会被重复计算。

记得没有满足条件的选择方案时，输出 -1。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,p;
int a[110],b[110],c[110],w[110];
int dp[110][110][110];
struct node{
	int x,y;
}t[110];
bool cmp(node x,node y){
	return x.x<y.x;
}
bool check(int x,int y){
	if(a[y]*t[x].x+b[y]*t[x].y<=c[y]) return 1;
	return 0;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>p;
	a[0]=b[0]=0,c[0]=-1e9,w[0]=0;
	for(int i=1;i<=n;i++){
		cin>>a[i]>>b[i]>>c[i]>>w[i];
	}
	for(int i=1;i<=p;i++){
		cin>>t[i].x>>t[i].y;
	}
	sort(t+1,t+1+p,cmp);
	for(int i=0;i<=p;i++){
		for(int j=0;j<n;j++){
			for(int k=j+1;k<=n;k++){
				dp[i][j][k]=1e9;
			}
		}
	}
	for(int i=0;i<n;i++){
		for(int j=i+1;j<=n;j++){
			dp[0][i][j]=w[i]+w[j];
		}
	}
	for(int i=1;i<=p;i++){
		for(int j=0;j<n;j++){
			for(int k=j+1;k<=n;k++){
				if(dp[i-1][j][k]==1e9) continue;
				if(check(i,j)||check(i,k)){
					dp[i][j][k]=min(dp[i][j][k],dp[i-1][j][k]);
					continue;
				}
				for(int l=1;l<=n;l++){
					if(l==j||l==k||!check(i,l)) continue;
					dp[i][min(l,j)][max(l,j)]=min(dp[i][min(l,j)][max(l,j)],dp[i-1][j][k]+w[l]);
					dp[i][min(l,k)][max(l,k)]=min(dp[i][min(l,k)][max(l,k)],dp[i-1][j][k]+w[l]);
				}
			}
		}
	}
	int ans=1e9;
	for(int i=0;i<n;i++){
		for(int j=i+1;j<=n;j++){
			ans=min(ans,dp[p][i][j]);	
		}
	}
	cout<<(ans==1e9?-1:ans);
	return 0;
}