自动搬运

查看原文

来自洛谷，原作者为

	PersistentLife **

搬运于2025-08-24 22:15:31，当前版本为作者最后更新于2020-04-14 13:45:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

博客体验更佳

提供一个样例

为方便大家调试程序，我以云剪贴板的形式提供一个比较强的样例：

输入 输出

展开源码复制即可。

前置芝士

图、树的基本概念，dfs，邻接表。

图、树的基本概念

这就是一张图：

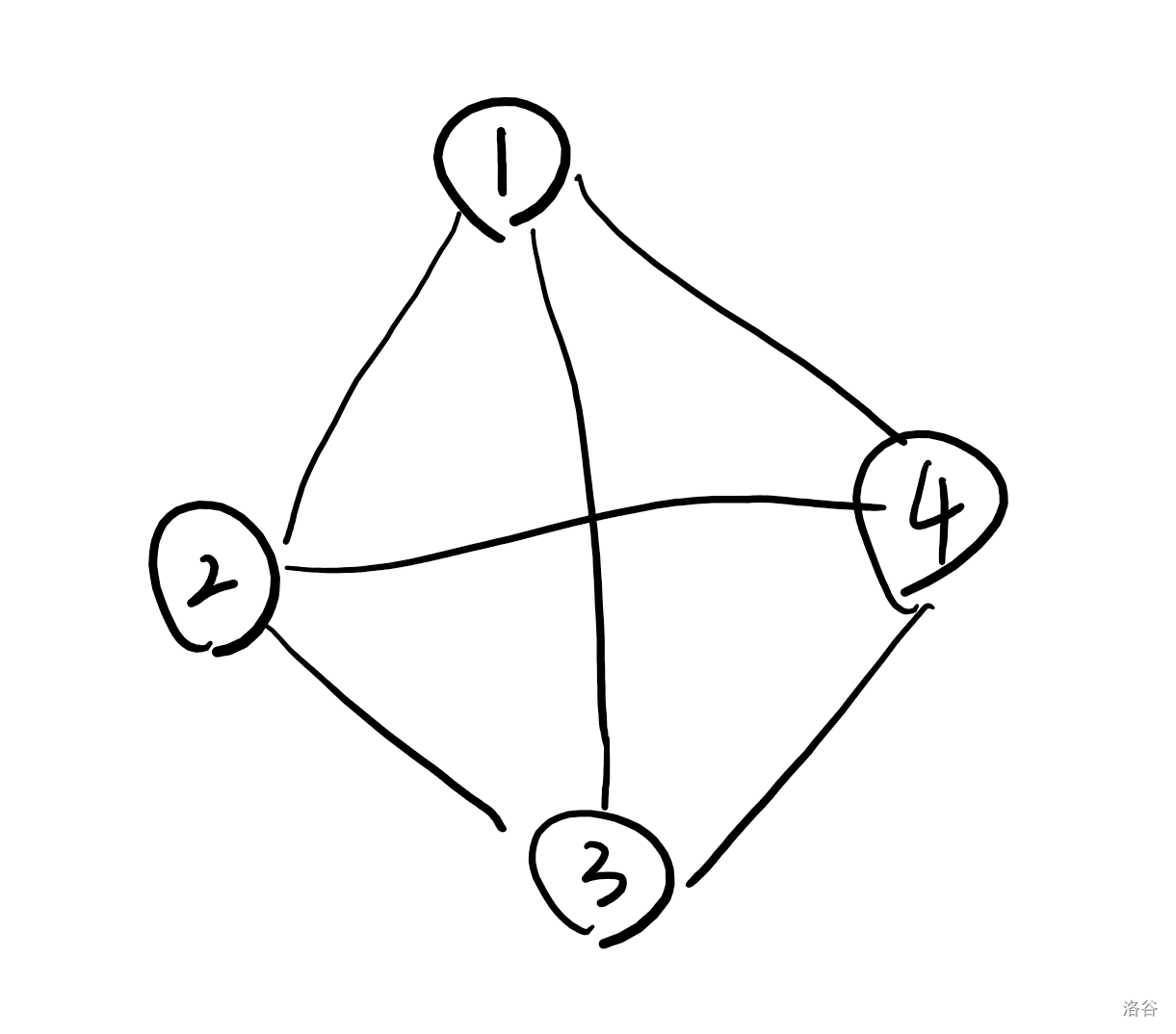
虽然这和我们之前看到的“图”不一样，但在离散数学里面，它就是一张图，研究“图”的离散数学分支就叫做“图论”。

在这张图中，①②③④就叫做节点，连接节点的线叫边。

当然，没有边只有节点的也叫图，没有节点但是有边的不叫图。

图有两种分类，上面的图叫“无向图”，下面这张图叫“有向图”：

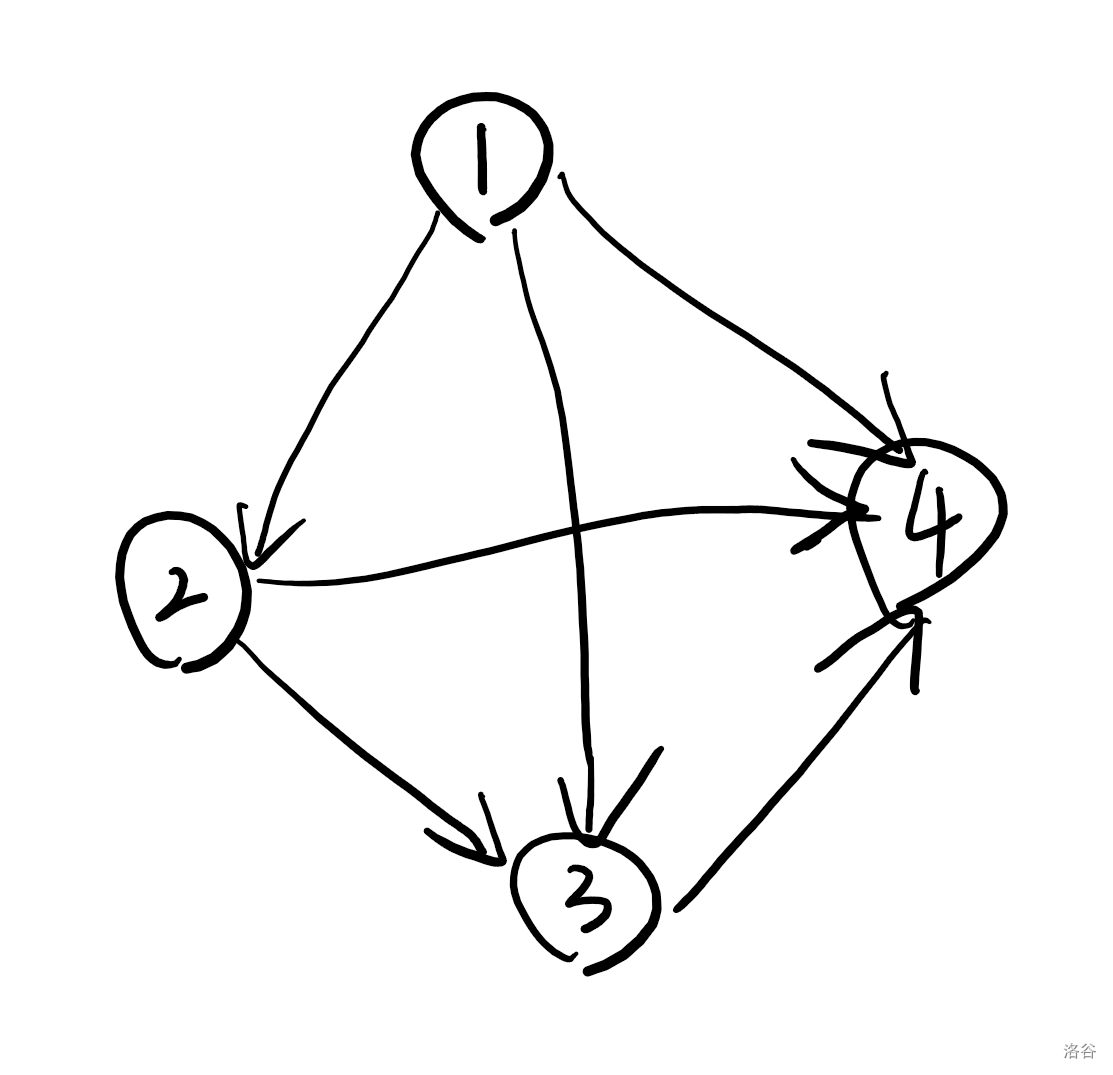
显然，有向图的边有方向，无向图的边没有方向，之后做题时题目会告诉你这是有向图还是无向图。

那么树是一种特殊的图，树是只由节点数 $-1$ 条边组成的连通图，那么这就是一棵树，这棵树也是样例里面的树：

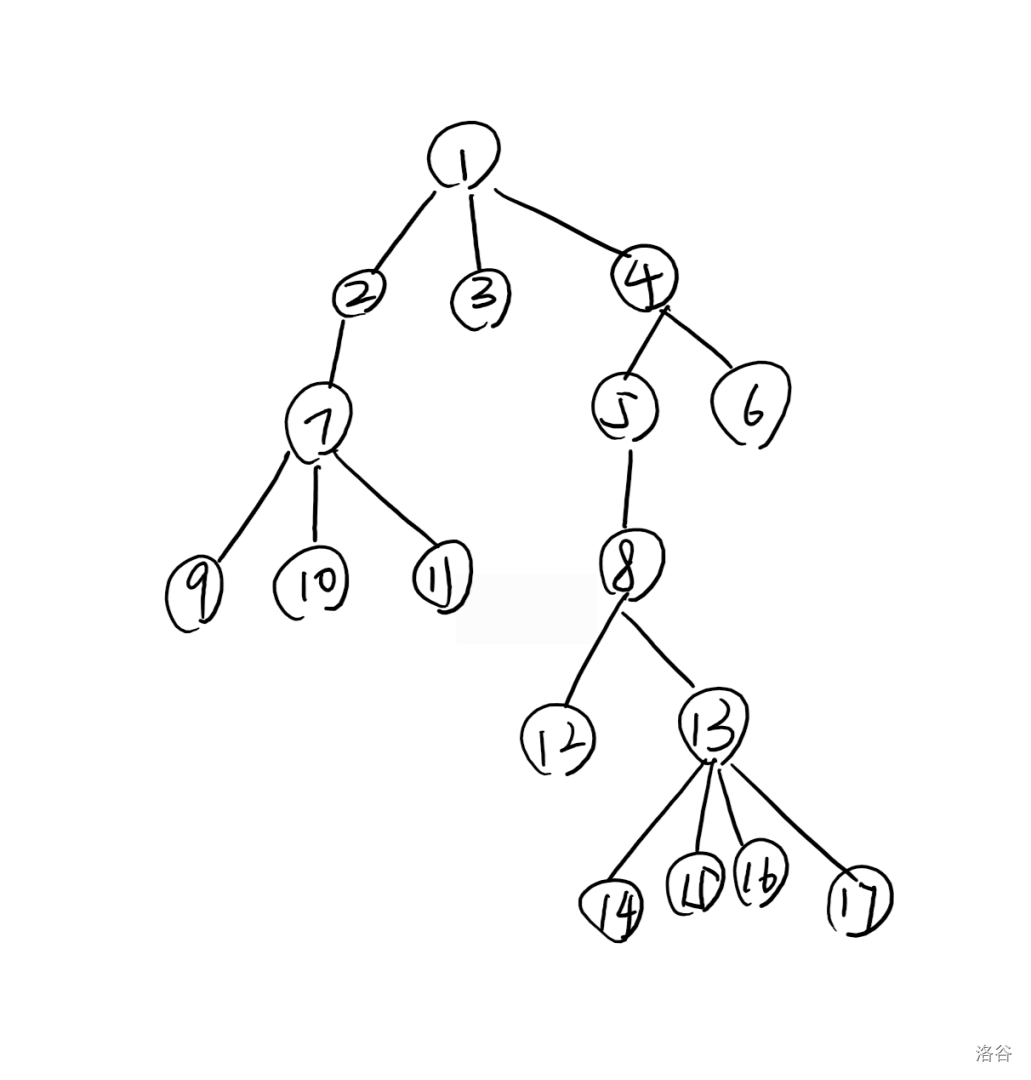
当然，有向图组成的树叫做“有根树”，无向图组成的就叫做“无根树”。

树根，就是没有“孩子”的节点。

一个节点的孩子，指有一条边从这个节点指向的节点，比如上图，②就是①的孩子，⑩是⑦的孩子。

那么父亲正好和孩子是反的，比如，①是②的父亲，⑦是⑩的父亲。

关于概念就介绍到这么多，如果大家想了解更多可以上网搜。

dfs

dfs是什么，是深度优先搜索，可以对图或树进行遍历，主要过程是“不撞南墙不回头”，即始终沿着一个方向走，直到没有可以遍历过的节点了，而且，遍历过的节点不会重复遍历。

例如上面这棵树的 dfs 序列就是：

$1-2-7-9-10-11-3-4-5-8-12-13-14-15-16-17-6$

还有一种遍历叫 bfs，即广度优先遍历，如果想了解可以做做 P5318 查找文献

邻接表

邻接表是一种可以存图的数据结构，因为树是一种特殊的图，所以也可以用邻接表存树。

邻接表是用 $vector$ 向量实现，每一个节点都有一个 $vector$，里面存储了与这个节点关联的节点，下面是实现邻接表的代码：

int a,b;
cin>>a>>b;//表示一条边的两个节点，g是全局的vector
g[a].push_back(b);
g[b].push_back(a);

此题代码实现

这题用 dfs，只是只要访问距离小于 $d$ 的节点，在 dfs 函数里面可以进行特判：

void dfs(int now,int dis)//分别表示现在的节点和距离
{
	vis[now]=1;//vis 数组标记节点是否被访问，以免重复统计
	if(dis==d) return;//是否达到了距离上限
	for(int i=0;i<g[now].size();i++)//枚举关联的所有节点
	{
		if(!vis[g[now][i]])//若没有访问过
		{
			dfs(g[now][i],dis+1);//就去跑一遍
			ans++;//答案加一
		}
	}
}

那么将邻接表和 dfs 组合到一起就是这题的代码：

#include<bits/stdc++.h>
using namespace std;
vector <int> g[123456];
bool vis[123456];
int ans,n,d;
void dfs(int now,int dis)
{
	vis[now]=1;
	if(dis==d) return;
	for(int i=0;i<g[now].size();i++)
	{
		if(!vis[g[now][i]])
		{
			dfs(g[now][i],dis+1);
			ans++;
		}
	}
}
int main()
{
	cin>>n>>d;
	for(int i=1;i<n;i++)
	{
		int a,b;
		cin>>a>>b;
		g[a].push_back(b);
		g[b].push_back(a);
	}
	dfs(1,0);
	cout<<ans;
	return 0;
}