自动搬运

查看原文

来自洛谷，原作者为

	阔睡王子 我回来了

搬运于2025-08-24 22:15:30，当前版本为作者最后更新于2020-10-07 17:22:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

回滚莫队

谢邀，人在机房，刚被机惨。

你是否在处理莫队删除操作的时候经常头疼，因为有的删除操作删掉之后就更新答案，如果你把它改成次大，那么你会发现改成次大之后再删除又需要次次大......

假使如果你吃了雄心豹子胆开满空间来存，不说这样看着很鸭儿蠢，空间直接变成平方级别，时间更不说了。根据莫队的排序特性，不知道是谁反正是个人搞了这个会滚的不删除莫队。

假如你也跟我一样不会让莫队滚，那么就让我跟你一起来学习如何让这个莫队滚起来。

我不会叫它“不删除莫队”,而是会叫它“能少删点就删点莫队”。因为这个算法名字涉嫌欺骗，很多时候我们都是尽可能减少删除操作,以更多的清空，增加操作，让连续工作的莫队有了喘气的机会，能重新处理一组一组的询问而不是一直删删删来处理所有的询问。喂莫队你要不要这么不持久。这样下来删除操作会变得没那么复杂，能让你更方便的实现。

那么是怎么实现的呢？

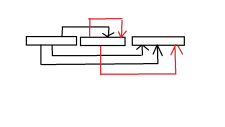
看一看这个不知道为什么这么小的图来想一想你之前写过的莫队，对于莫队一个一个的询问，我们会让 L R 指针不断地移动，在每个询问之间反复横跳，加以不断的删除，添加操作来得出答案。

然后为了避免删除操作，我们可以想一想能不能找到几个为一组的询问中的一个公共的线段，每次就让这个公共线段的 L R 分别向左右移动来和询问的左右端点重合来得出答案，而不是删过来删过去。

这个思路就是回滚莫队的核心思路。

可能你没有很好地理解，再给你一组有序的数据的几张图来演示这个处理过程：

你就会发现，哇哦，居然是这么清晰。

于是我们继续想，怎么处理几个交叉，并不那么有序的询问呢？

设左端点在一个块以内的所有询问构成一组询问。

根据莫队排序后的一组询问的右端点是有序的，就先不管右端点了。

然后可知对于这一组询问，它们的左端点无序，但是都在同一个块以内。

我们可以像这样来做：

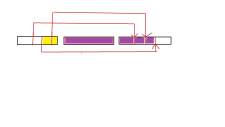
我们可以让 L 停留在这组询问左端点所在块的最右方， R 不断的向右移动处理询问。对于每个询问的左端点就定义一个新的临时指针 p 和一套新的临时数组从L开始向左移动处理询问，L 不变， p 处理完事后就回来，回来的路上顺手把来时存的临时数组清空。

图中黄色区间就是 p 处理的区域，剩余有色区域的都是 R 处理的(注意上图中R并非每次都回到 L 这里，而是从上一次 R 的位置开始移动，这里可能让您产生理解误差)。

而每换成另外一组询问的时候请空数组，重新设定 L,R 就行了，这就是回滚莫队了。

代码的注释也写了很多:

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn=2e5+10;
//以下是变量表 
int n,m,len;
//len是块的大小 
int a[maxn],b[maxn];
//a:离散化后的数组
//b:block简写,表示给定下标对应的块 
int R[maxn]; 
//每个块的右端 
int ans[maxn];
//离线操作用来存储答案 
int st[maxn],ed[maxn],ed2[maxn];
//得出答案时需要用到的桶
//代表意义分别为在给定范围内: 
//元素出现的第一个位置
//元素出现的最后一个位置
//在每组询问的公共起点(某个块的右端)前的一段中,元素出现的最后一个位置 
inline int read()
{
	int num=0;
	char ch=getchar();
	while(ch>57||ch<48)ch=getchar();
	do num=(num<<1)+(num<<3)+(ch^48),ch=getchar(); while(ch>47&&ch<58);
	return num;
}
struct lsh
{int id,x;}tmp[maxn];
bool lsh_cmp(lsh x,lsh y)
{return x.x<y.x;}
//离散化 
struct query
{int l,r,id;}q[maxn];
bool query_cmp(query x,query y)
{return (b[x.l]==b[y.l])?x.r<y.r:b[x.l]<b[y.l];}
//存储询问以及把询问排序 
void datain()//读入并处理一部分数据 
{
	n=read();
	len=sqrt(n); 
	for(int i=1;i<=n;i++)
	{
		tmp[i].x=read();
		tmp[i].id=i;
		b[i]=(i-1)/len+1;
	}
	for(int i=1;i<=b[n];i++)//处理出每个块的右端 
	R[i]=(i==b[n])?n:len*i;//记录下这个右端！ 
	m=read();
	for(int i=1;i<=m;i++)
	{
		q[i].l=read();q[i].r=read();
		q[i].id=i;
	}
	sort(q+1,q+m+1,query_cmp);
}
void lsh() 
{
	sort(tmp+1,tmp+n+1,lsh_cmp);//排序然后离散化啦 
	int pre=-1,cnt=0;//喜欢的离散化写法 
	for(int i=1;i<=n;i++)
	{
		if(tmp[i].x!=pre)cnt++;
		a[tmp[i].id]=cnt;//投射回去,让a[1]~a[n]变成离散化数组 
		pre=tmp[i].x;
	}
}
void work()//开始处理询问 
{
	int block=0,tmp1=0,l=0,r=0;
	//block:块,代表上次询问左端点在哪个块
	//如果块一样我们就可以直接使用上次留下来的进程 
	//不一样就舍弃上次的进程,全部推翻
	//tmp1:在公共L到上一次询问R时得出的答案
	//l:公共L
	//r:上一次询问的R 
	for(int i=1;i<=m;i++)
	{
		if(b[q[i].l]==b[q[i].r])
		//如果是同一个块就没有什么好说的了 
		//你的莫队技巧全部木大,还不如暴力求解，时间复杂度不会退化 
		{
			tmp1=0;
			for(int j=q[i].l;j<=q[i].r;j++)st[a[j]]=0;
			//你只需要用到st，就只清空st
			//诶你可能会想:st清空了,l,r没动,那后面求解不就乱套了？ 会不会调用到错误的st 
			//不会的
			//你想一想，询问左右端点变成在一个块时,是什么时候
			//是左端点所在块已经不同于之前的块的时候啊! 
			//是你前面求出的tmp1,st,ed已经失去利用价值的时候啊! 
			//肯定后面需要清空(摈弃)之前的数组，开始解新一组的询问
			//那么之后的l,r,st,肯定会清空掉 
			//总而言之：我这里清空st,根本就不影响之后啊哈哈哈哈哈反正都会清空 
			//听不懂就算了... 
			for(int j=q[i].l;j<=q[i].r;j++)
			{		
				if(!st[a[j]])st[a[j]]=j;
				tmp1=max(tmp1,j-st[a[j]]);
			}
			for(int j=q[i].l;j<=q[i].r;j++)st[a[j]]=0;
			ans[q[i].id]=tmp1;
			continue ;
		}
		//要开始正常求解了 
		int now=b[q[i].l];//先记录下左端点所在的块，偷懒嗷 
		if(block!=now)//左端点所在块发生变化了 
		{
			tmp1=0;
			for(int j=l;j<=r;j++)st[a[j]]=ed[a[j]]=0;//之前求解的玩意儿都不要了,这里没用 
			//从头开始算 
			l=R[now];
			r=l-1;//莫队细节：记得r=l-1； 
			block=now;//更新所在块 
		}
		while(r<q[i].r)
		{
			r++;
			if(!st[a[r]])st[a[r]]=r;//st(start:元素第一次出现的位置)只需要更新一次 
			ed[a[r]]=r;//从前移向后,ed(end:元素最后出现的位置)要一直更新 
			tmp1=max(tmp1,r-st[a[r]]);//更新答案 
		}
		//公共左端点到r的答案处理出来了,你还记得前面的有一小端还没有算吗 
		int p=l,tmp2=0;
		while(q[i].l<p)
		{
			p--;
			if(!ed2[a[p]])ed2[a[p]]=p;//从后向前移动,ed更新一次就够了嗷 
			//防止想怎么撤回想出脑膜炎,直接开个临时数组记录一下新的ed就行 
			tmp2=max(tmp2,max(ed[a[p]],ed2[a[p]])-p);//细节:记得取个max,你公共左端点右边也可能出现这个元素 
		}
		while(p<l)//算完了就撤回 
		{
			ed2[a[p]]=0;
			p++;
		}
		ans[q[i].id]=max(tmp2,tmp1);//在公共左端点左右答案中取个max 
	}
}
int main()
{
	datain(); 
	lsh();
	work();
	for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
}