1 条题解
-
0
自动搬运
来自洛谷,原作者为

StudyingFather
在纷繁杂乱的世界里,独自寻找属于自己的光荣与梦想。搬运于
2025-08-24 22:15:29,当前版本为作者最后更新于2019-10-28 19:15:45,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
Johnson 和 Floyd 一样,是一种能求出无负环图上任意两点间最短路径的算法。该算法在 1977 年由 Donald B. Johnson 提出。
1 算法概述
任意两点间的最短路可以通过枚举起点,跑 次 Bellman-Ford 算法解决,时间复杂度是 的,也可以直接用 Floyd 算法解决,时间复杂度为 。
注意到堆优化的 Dijkstra 算法求单源最短路径的时间复杂度比 Bellman-Ford 更优,如果枚举起点,跑 次 Dijkstra 算法,就可以在 (本文中的 Dijkstra 采用
priority_queue实现,下同)的时间复杂度内解决本问题,比上述跑 次 Bellman-Ford 算法的时间复杂度更优秀,在稀疏图上也比 Floyd 算法的时间复杂度更加优秀。但 Dijkstra 算法不能正确求解带负权边的最短路,因此我们需要对原图上的边进行预处理,确保所有边的边权均非负。
一种容易想到的方法是给所有边的边权同时加上一个正数 ,从而让所有边的边权均非负。如果新图上起点到终点的最短路经过了 条边,则将最短路减去 即可得到实际最短路。
但这样的方法是错误的。考虑下图:
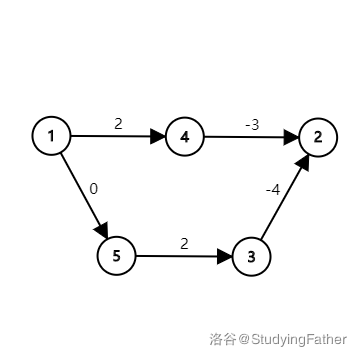
的最短路为 ,长度为 。
但假如我们把每条边的边权加上 呢?
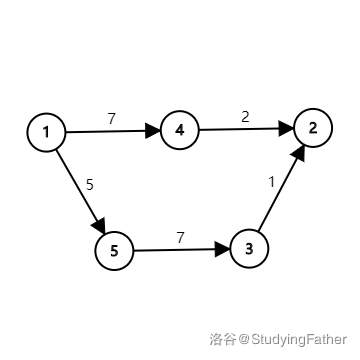
新图上 的最短路为 ,已经不是实际的最短路了。
Johnson 算法则通过另外一种方法来给每条边重新标注边权。
我们新建一个虚拟节点(在这里我们就设它的编号为 )。从这个点向其他所有点连一条边权为 的边。
接下来用 Bellman-Ford 算法求出从 号点到其他所有点的最短路,记为 。
假如存在一条从 点到 点,边权为 的边,则我们将该边的边权重新设置为 。
接下来以每个点为起点,跑 轮 Dijkstra 算法即可求出任意两点间的最短路了。
容易看出,该算法的时间复杂度是 。
Q:那这么说,Dijkstra 也可以求出负权图(无负环)的单源最短路径了?
A:没错。但是预处理要跑一遍 Bellman-Ford,还不如直接用 Bellman-Ford 呢。2 正确性证明
为什么这样重新标注边权的方式是正确的呢?
在讨论这个问题之前,我们先讨论一个物理概念——势能。
诸如重力势能,电势能这样的势能都有一个特点,势能的变化量只和起点和终点的相对位置有关,而与起点到终点所走的路径无关。
势能还有一个特点,势能的绝对值往往取决于设置的零势能点,但无论将零势能点设置在哪里,两点间势能的差值是一定的。
接下来回到正题。
在重新标记后的图上,从 点到 点的一条路径 的长度表达式如下:
$(w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+ \dots +(w(p_k,t)+h_{p_k}-h_t)$
化简后得到:
无论我们从 到 走的是哪一条路径, 的值是不变的,这正与势能的性质相吻合!
为了方便,下面我们就把 称为 点的势能。
上面的新图中 的最短路的长度表达式由两部分组成,前面的边权和为原图中 的最短路,后面则是两点间的势能差。因为两点间势能的差为定值,因此原图上 的最短路与新图上 的最短路相对应。
到这里我们的正确性证明已经解决了一半——我们证明了重新标注边权后图上的最短路径仍然是原来的最短路径。接下来我们需要证明新图中所有边的边权非负,因为在非负权图上,Dijkstra 算法能够保证得出正确的结果。
根据三角形不等式,新图上任意一边 上两点满足: 。这条边重新标记后的边权为 。这样我们证明了新图上的边权均非负。
至此,我们就证明了 Johnson 算法的正确性。
3 参考代码
(被各位 D 惨了,所以把代码扔到 clang-format 里格式化了下 /wq)
#include <cstring> #include <iostream> #include <queue> #define INF 1e9 using namespace std; struct edge { int v, w, next; } e[10005]; struct node { int dis, id; bool operator<(const node& a) const { return dis > a.dis; } node(int d, int x) { dis = d, id = x; } }; int head[5005], vis[5005], t[5005]; int cnt, n, m; long long h[5005], dis[5005]; void addedge(int u, int v, int w) { e[++cnt].v = v; e[cnt].w = w; e[cnt].next = head[u]; head[u] = cnt; } bool spfa(int s) { queue<int> q; memset(h, 63, sizeof(h)); h[s] = 0, vis[s] = 1; q.push(s); while (!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for (int i = head[u]; i; i = e[i].next) { int v = e[i].v; if (h[v] > h[u] + e[i].w) { h[v] = h[u] + e[i].w; if (!vis[v]) { vis[v] = 1; q.push(v); t[v]++; if (t[v] == n + 1) return false; } } } } return true; } void dijkstra(int s) { priority_queue<node> q; for (int i = 1; i <= n; i++) dis[i] = INF; memset(vis, 0, sizeof(vis)); dis[s] = 0; q.push(node(0, s)); while (!q.empty()) { int u = q.top().id; q.pop(); if (vis[u]) continue; vis[u] = 1; for (int i = head[u]; i; i = e[i].next) { int v = e[i].v; if (dis[v] > dis[u] + e[i].w) { dis[v] = dis[u] + e[i].w; if (!vis[v]) q.push(node(dis[v], v)); } } } return; } int main() { ios::sync_with_stdio(false); cin >> n >> m; for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; addedge(u, v, w); } for (int i = 1; i <= n; i++) addedge(0, i, 0); if (!spfa(0)) { cout << -1 << endl; return 0; } for (int u = 1; u <= n; u++) for (int i = head[u]; i; i = e[i].next) e[i].w += h[u] - h[e[i].v]; for (int i = 1; i <= n; i++) { dijkstra(i); long long ans = 0; for (int j = 1; j <= n; j++) { if (dis[j] == INF) ans += j * INF; else ans += j * (dis[j] + h[j] - h[i]); } cout << ans << endl; } return 0; }4 应用
虽然算法名告诉我们它可以用于求解全源最短路,但是实际场景中需要求解全源最短路的场合并不太多。
在费用流问题中,存在思想类似的 Primal-Dual 原始对偶算法。它通过类似的方法将所有边的边权转为非负值,从而可以使用 Dijkstra 算法求出残量网络上的最短增广路。
Reference
- Johnson's algorithm - Wikipedia
- 《算法导论(中译本,第 3 版)》,25.3 用于稀疏图的 Johnson 算法,409-411 页
- 1
信息
- ID
- 4906
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
