1 条题解
-
0
自动搬运
来自洛谷,原作者为

Hanx16Kira
AFOed搬运于
2025-08-24 22:15:24,当前版本为作者最后更新于2022-11-08 21:04:57,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
P5897 [IOI2013]wombats
%你赛的 T4,写一下题解来加深记忆。
在 NOIP 模拟赛里面放 IOI 的题,出题人真有你的(考虑设计一种 DP 状态。定义 表示从 行的第 个到 行 个的最短距离,那么会发现这个状态是可以拆分成为两个等大的子问题 $f(s,m,i,k),f(m,t,k,i)(m=\displaystyle\frac {s + t}2)$ 进行解决,也就是说这个状态设计使得我们可以用线段树维护这一转移。
考虑怎么从 转移到 ,可以直接枚举 进行转移,这样的转移复杂度是 的,需要优化。注意到这个状态是满足决策单调性的,证明很简单(如图所示,一目了然):
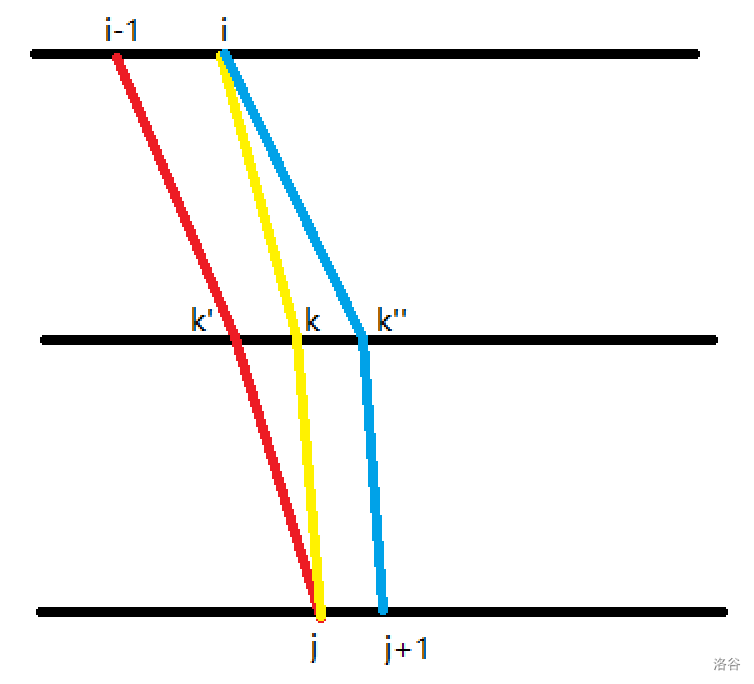
假设 的决策点是 ,那么一定有 ,所以每次枚举 只需要在 内枚举即可,时间复杂度均摊下来就少了一个 ,变成了 。
这下就可以用线段树维护了,每次合并的复杂度是 ,建树的总时间复杂度就是 ,每次修改操作的时间复杂度是 ,时间上应该可以过。
本以为这样就解决了,然后看到空间限制 256MB,这个做法的空间复杂度是 的,极限数据下到了 ,稳稳的爆炸,因此还需要考虑怎么优化。
一个很巧妙的方式就是将线段树的叶子节点维护的区间长度变成一个阈值 ,而非原来的 。这样做就类似分块的思想了,对于每一次修改,对叶子节点上的块进行暴力更改,然后对于整块之间的合并用线段树维护。这样可以大大减少线段树上的节点个数,从而减少了空间复杂度。
块内的暴力修改时间复杂度是 的,所以建树的总时间复杂度是 $\displaystyle\mathcal O(\frac rlc^2(\log \frac rl + l))$,每一次修改的时间复杂度是 ,空间复杂度与建树的时间复杂度同阶。实际测试中, 的时候可以取得比较不错的效果,在空间和时间的均衡上很不错。
Code
#include<bits/stdc++.h> using namespace std; namespace Hanx16qwq { constexpr int _N = 5e3 + 5, _M = 2e2 + 5, _B = 1e3 + 5; int len = 25, n, m, q; int d[_N][_M], v[_N][_M]; int pos[_N + 5], bl[_B + 5], br[_B + 5], cnt; int p[_M + 5][_M + 5]; class Node { // 线段树上节点的类 public: int f[_M][_M]; // 上面的 f,只不过省略了 s 和 t Node() {memset(f, 0x3f, sizeof f);} void Update(int s, int t) { // 块内暴力 for (int i = 1; i <= m; i++) { for (int j = i, res = 0; j <= m; j++, res += d[s][j - 1]) f[i][j] = res; // 向右 for (int j = i, res = 0; j >= 1; j--, res += d[s][j]) f[i][j] = res; // 向左 for (int j = 1; j <= m; j++) f[i][j] += v[s][j]; // 向下 for (int k = s + 1; k <= t; k++) { for (int j = 2; j <= m; j++) f[i][j] = min(f[i][j], f[i][j - 1] + d[k][j - 1]); // 向右 for (int j = m - 1; j ; j--) f[i][j] = min(f[i][j], f[i][j + 1] + d[k][j]); // 向左 for (int j = 1; j <= m; j++) f[i][j] += v[k][j]; // 向下 } } } }T[_B]; void Maintain(Node &res, Node a, Node b) { // 合并 Node ans; for (int i = 1; i <= m; i++) // s 处的起点 for (int j = m; j >= 1; j--) { // t 处的终点 int st = p[i - 1][j] ? p[i - 1][j] : 1; int ed = p[i][j + 1] ? p[i][j + 1] : m; for (int k = st; k <= ed; k++) // 决策单调性 if (ans.f[i][j] > a.f[i][k] + b.f[k][j]) ans.f[i][j] = a.f[i][k] + b.f[k][j], p[i][j] = k; // 记录决策点 } res = ans; } #define LC (k << 1) #define RC (k << 1 | 1) #define mid ((l + r) >> 1) void Build(int k, int l, int r) { if (l == r) return T[k].Update(bl[l], br[l]); // 叶子节点直接暴力做 Build(LC, l, mid), Build(RC, mid + 1, r); Maintain(T[k], T[LC], T[RC]); // 合并 } void Modify(int k, int l, int r, int p) { if (l == r && l == p) return T[k].Update(bl[l], br[l]); // 同上 if (l > p || r < p) return; Modify(LC, l, mid, p), Modify(RC, mid + 1, r, p); Maintain(T[k], T[LC], T[RC]); } void main() { ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j < m; j++) cin >> d[i][j]; for (int i = 1; i < n; i++) for (int j = 1; j <= m; j++) cin >> v[i][j]; cnt = (n - 1) / len + 1; // 总块数 for (int i = 1; i <= cnt; i++) bl[i] = (i - 1) * len + 1, br[i] = min(i * len, n); // 预处理块的边界 for (int i = 1; i <= cnt; i++) for (int j = bl[i]; j <= br[i]; j++) pos[j] = i; // 每个点所在的块编号(正常分块写法) Build(1, 1, cnt); cin >> q; for (int i = 1; i <= q; i++) { static int opt, a, b; cin >> opt >> a >> b; a++, b++; if (opt == 1) { cin >> d[a][b]; Modify(1, 1, cnt, pos[a]); } else if (opt == 2) { cin >> v[a][b]; Modify(1, 1, cnt, pos[a]); } else { cout << T[1].f[a][b] << '\n'; // 答案就在线段树顶 } } } } signed main() { Hanx16qwq::main(); return 0; }
- 1
信息
- ID
- 4895
- 时间
- 8000ms
- 内存
- 250MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
