自动搬运

查看原文

来自洛谷，原作者为

	清平乐 愿你——来时不惧风雨，去时不畏人言

搬运于2025-08-24 22:15:15，当前版本为作者最后更新于2020-08-26 11:23:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这是一道构造题

构造出来后巨水，但要是想不到就GG

不妨将这个图考虑成树，只有当树上的每条边都被询问后才知道这棵树是否联通

那我们现在尽量让树的边最后被询问到就行了

也就是说我们让每个点最后被询问到的边成为树边就ok了

比如下面这张图，红色的边为每个点最后被询问到的边，红边就构成了一棵生成树

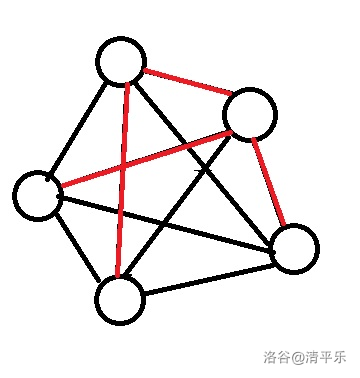
下面考虑代码实现，$n$ 个节点的完全图中有 $\frac{n(n-1)}{2}$ 条边，考虑以 $0$ 为根，第 $i$ 个点的父亲规定只能是编号比 $i$ 小的点，显然这样的边有 $i$ 条，如此总边数依然是 $\frac{n(n-1)}{2}$

那么对于这 $i$ 条边，我们保留最后出现的那一条的端点为 $i$ 的父亲。这样的话，只有到第 $\frac{n(n-1)}{2}$ 个询问，我们才能知道最后一个点的父亲，才能确定图的联通性。

代码真的很短。。。

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;

int n,r,u,v;
int deg[1005];

int main(void)
{
	scanf("%d",&n);
	r=n*(n-1)>>1;
	while(r--)
	{
		scanf("%d%d",&u,&v);
		if(u<v) swap(u,v);
		printf("%d\n",++deg[u]==u);
	}
	return 0;
}