自动搬运

查看原文

来自洛谷，原作者为

	鏡音リン 希望大家都能成为自己想要的样子呐

搬运于2025-08-24 22:15:14，当前版本为作者最后更新于2019-12-31 11:35:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题链接

题意：

给 $n$ 个液体分组，要求对于任意不同组液体 $i,j$ 有 $gcsd(a_i,a_j)\le x^2$。求最大的组数，满足组数最大的条件下求每组 $c_i$ 的最大值的和。有多组询问，每次给定 $x$。

首先，$\operatorname{gcsd}$？那是啥？

按照题目描述里说的，如果定义 $h(x)$ 表示 $\sqrt x$ 的整数因式部分，那么 $gcsd(x,y)=h(\gcd(x,y))^2$

可以看出这玩意也就等于 $\gcd(h(x),h(y))^2$。于是原条件就等价于 $\gcd(h(a_i),h(a_j))\le x$，考虑用 $h(a_i)$ 代替原题中的 $a_i$ 进行计算

另一个问题是求 $c_i$，$c_i$ 定义为 $b_i$ 分解成质因数后最大的指数。

$h(a_i)$ 和 $c_i$ 都可以用线性筛来求，那么我们的线性筛需要筛四个东西

$s[x]$：$x$ 的最小质因子

$st[x]$：$x$ 分解成质因数后 $s[x]$ 的指数

$sm[x]$：$x$ 分解成质因数后最大的指数

$h[x]$：$\sqrt x$ 的整数因式部分

std::vector<int> pr;
int s[M], h[M], st[M], sm[M];
void prime() {
	for (int i = 2; i < M; i++) {
		if (!s[i]) { //i是一个质数
			pr.push_back(i);
			s[i] = i;
			st[i] = sm[i] = h[i] = 1;
		}
		for (int j : pr) { //j是i*j的最小质因子
			if (i*j >= M) break;
			s[i*j] = j;
			st[i*j] = (s[i] == j) ? st[i]+1 : 1;
			h[i*j] = (s[i] == j && st[i] & 1) ? h[i]*j : h[i];
			sm[i*j] = std::max(sm[i], st[i*j]);
			if (i % j == 0) break;
		}
	}
}

接下来考虑进一步转化问题。刚才我们说，对于任意不同组液体 $i,j$ 有 $\gcd(h(a_i),h(a_j))\le x$

再换句话，如果 $\gcd(h(a_i),h(a_j))> x$，那么 $i,j$ 必须在同一组

这样的描述可以转化为图论模型：每种液体是一个节点，如果 $\gcd(h(a_i),h(a_j))> x$ 则节点 $i$ 和 $j$ 之间连一条边。很显然一个连通块内的节点必须在同一组，既然我们要组数最大，那么每个连通块是一组就是最优方案。最大的组数也就是连通块个数，实验得分也很好求，找到每个连通块内最大的 $c_i$ 然后加起来。

举个例子，当 $x=2$ 的时候样例大概长这样（点上的数字就是 $a_i$）

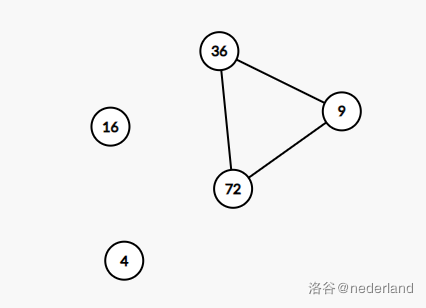
于是我们就有了最暴力的算法：对于每个 $x$，$O(n^2)$ 暴力建图，dfs 找连通块，时间复杂度 $O(mn^2)$。打上这个应该就可以拿 30 分。

不过，我们发现，这张图里很多点实际都是没有用的。所有 $h(a_i)\le x$ 的点就是没有用的，它们都没有连边，都可以单独一组直接计入答案。可以预处理出每个 $x$，$h(a_i)\le x$ 的点对答案的贡献，这样建图的时候就不用考虑这些点了。

另一方面，对于 $h(a_i)>x$ 的点，如果有很多个点的 $h(a_i)$ 相等，那么这些点都必须在同一组，其中 $c_i$ 最大的那个可能计入贡献。不妨把它们当作一个点，这个点的 $c_i$ 就是原来那些点 $c_i$ 的最大值。

可以考虑按照 $h(a_i)$ 把所有点分类，由于 $h(a_i)\le \sqrt{a_i} \le 200$，那么最多也就只有 $200$ 类，也就是图上最多有 $200$ 个点。而且枚举 $x$ 也只需要枚举到 $\max\{h(a_i)\}$，这个时候建图应该可以 AC 此题了。代码就不放了。

但是这样复杂度是 $O(a^\frac{3}{2})$，并不是最优复杂度，如果 $a$ 的范围是 $2\times 10^7$ 就没了。

可以考虑从 $\max\{h(a_i)\}$ 开始，从大到小枚举 $x$。这样相当于在图上不断加边，连通块可以用并查集维护。具体实现可以在计算完 $x$ 的答案之后，把所有 $x$ 的倍数合并起来。时间复杂度 $O(\sqrt a \log^2a)$，低于线性复杂度，所以实际上复杂度的瓶颈是线性筛，总体复杂度应该是 $O(n+m+\max\{a_i\}+\max\{b_i\})$。

注意到如果使用线性筛，本题的内存非常的卡，所以我做了一些卡内存的小优化：把 $st$ 和 $sm$ 的内存空间合并到一起，并使用 char 类型，也就是先求一遍 $st$，再在原位求 $sm$，具体可以看代码，对比一下最终代码和上面那一段代码的区别部分。

完整代码

#include <cstdio>
#include <vector>
#define N 200000
#define M 20000001
#define R 201
#define L 40001
std::vector<int> pr;
int s[M], h[L]; char st[M];
void prime() {
    for (int i = 2; i < M; i++) {
        if (!s[i]) {
            pr.push_back(i);
            s[i] = i;
            st[i] = 1;
            if (i < L) h[i] = 1;
        }
        for (int j : pr) {
            if (i*j >= M) break;
            s[i*j] = j;
            st[i*j] = (s[i] == j) ? st[i]+1 : 1;
            if (i*j < L) h[i*j] = (s[i] == j && st[i] & 1) ? h[i]*j : h[i];
            
            if (i % j == 0) break;
        }
    }
    for (int i = 2; i < M; i++) {
        for (int j : pr) {
            if (i*j >= M) break;
            st[i*j] = std::max(st[i], st[i*j]);
            if (i % j == 0) break;
        }
    }
}
struct pair {int x, y; };
pair operator + (pair a, pair b) {
    return (pair) {a.x + b.x, a.y + b.y};
}
int n, m, a[N], b[N], mv[R], f[R], p[R];
pair co[R], ans[R], cnt;
int fa(int x) {
    return x == f[x] ? x : f[x] = fa(f[x]);
}
int main() {
    prime();
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++)
        scanf("%d", a+i);
    for (int i = 0; i < n; i++) {
        scanf("%d", b+i);
        a[i] = h[a[i]];
        b[i] = st[b[i]];
        co[a[i]] = co[a[i]] + (pair) {1, b[i]};
        mv[a[i]] = std::max(mv[a[i]], b[i]);
    }
    for (int i = 2; i < R; i++)
        co[i] = co[i] + co[i-1];
    for (int i = R-1; i >= 2; i--) {
        ans[i] = co[i]+cnt;
        bool mg = false;
        f[i] = i; p[i] = mv[i];
        cnt = cnt + (pair) {1, mv[i]};
        for (int j = 2; i*j < R; j++) if (mv[i*j]) {
            int x = fa(i), y = fa(i*j);
            if (x != y) {
                mg = true;
                f[x] = y;
                cnt.x--;
                cnt.y -= std::min(p[x], p[y]);
                p[y] = std::max(p[x], p[y]);
            }
        }
        if (!mv[i] && !mg) cnt.x--;
    }
    while (m--) {
        int x; scanf("%d", &x);
        pair p = (x < R) ? ans[x] : co[R-1];
        printf("%d %d\n", p.x, p.y);
    }
}