自动搬运

查看原文

来自洛谷，原作者为

	xiaolilsq 灰名不比红名好看（

搬运于2025-08-24 22:15:07，当前版本为作者最后更新于2020-07-11 17:08:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目链接

题目分析

考虑什么时候选出来的点才是独立支配集。

首先，所有选出来的点的值肯定单调递增，如果存在一个地方值减小了，那么选出的这两个点就肯定有连边，不满足独立集的要求。

也就是说，我们选出来的肯定是一个单调递增子序列。

如何才能满足支配集这个要求？考虑何时一个点不会被支配：

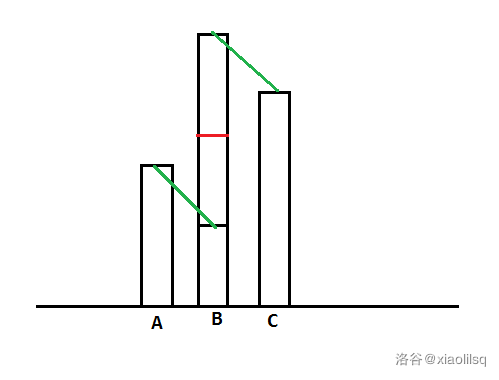
（其中 $A,B,C$ 为下标，矩形高度表示值，绿色的线为连边）

如果 $A,C$ 都被选入了点集，那么当且仅当 $B$ 的值在红色区域时 $B$ 才不能不选，此时 $B$ 是可以加入到这个单调递增子序列的。

也就是说，我们要选出来的是一个极大的单调递增子序列！（认为一个单调递增子序列是极大的当且仅当无法再往里面加入数）

此时就可以 $dp$ 做了，设 $dp_i$ 表示仅考虑 $1$ 到 $i$ 时将 $i$ 作为序列终点的极大单调递增子序列的数量，那么转移（ $a_i$ 表示排列中下标为 $i$ 的数）：

$$dp_i=\begin{cases}1 &\ \max_{j=1}^{i-1}(a_j)>a_i \\ \sum_{1\le j\le i-1 \&\& \text{不存在一个位置}k(j<k<i)\text{使得}a_j<a_k<a_i}dp_j &\ {\rm otherwise} \end{cases} $$

直接 $\mathcal O(n^2)$ 扫就可以了。

然后 $dp_i$ 可以被累加进答案当且仅当 $a_i>\max_{j=i+1}^n(a_j)$ 。

如何根据逆序对图还原排列？根据逆序对图得出每个数 $i$ 在 $i\dots n$ 中的排名，然后从后往前扫一遍一个个插入即可，模拟 $\mathcal O(n^2)$ （不妨写个 $\rm Splay$ 优化复杂度？）。

参考代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
	int f;char c;
	for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
	static char q[64];int cnt=0;
	if(!x)pc('0');if(x<0)pc('-'),x=-x;
	while(x)q[cnt++]=x%10+'0',x/=10;
	while(cnt--)pc(q[cnt]);
}
const int maxn=105;
int d[maxn],pos[maxn],id[maxn];
long long dp[maxn];
int main(){
	int n,m;
	read(n),read(m);
	for(int i=1;i<=m;++i){
		int u,v;
		read(u),read(v);
		if(u>v)u^=v^=u^=v;
		++d[u];
	}
	for(int i=n;i>=1;--i){
		++d[i];
		for(int j=n-i+1;j>d[i];--j)
			pos[j]=pos[j-1];
		pos[d[i]]=i;
	}
	for(int i=1;i<=n;++i)
		id[pos[i]]=i;
	for(int i=1;i<=n;++i){
		int mx=0;
		for(int j=i-1;j>=1;--j){
			if(id[j]<id[i]&&id[j]>=mx){
				mx=id[j];dp[i]+=dp[j];
			}
		}
		if(!dp[i])dp[i]=1;
	}
	int mx=0;long long ans=0;
	for(int i=n;i>=1;--i)
		if(id[i]>=mx)
			mx=id[i],ans+=dp[i];
	write(ans),pc('\n');
	return 0;
}