自动搬运

查看原文

来自洛谷，原作者为

	icaijy **

搬运于2025-08-24 22:14:57，当前版本为作者最后更新于2024-12-21 22:35:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这道题难点是想清楚最佳情况该怎么走。首先我们观察到要想走的越少，我们每次肯定会拿足物品，并且全部发放完才回来。这个很好理解，因为拿多一点物品并不会有什么代价，我们也不会还剩着东西就走回来，否则我们还得拿东西再走一趟这样得走更久。

第二是我们不会跳过人不给，因为跑到远处回来再补上跳过的人，和连续给完回来再跑到远处是一样的。以上总结一下就是每次我们会拿足 $K$ 个纪念品并且分给连续的 $K$ 个人，直到大家都有纪念品。

其次我们观察到大多数情况都是从哪出发，送完后从哪原路返回。而只有一种情况是会走一周回到原点，就是送完东西已经超过了中点了，这样原路返回就不如继续走完回来了。

走一周这个动作我们至多只会做一次。因为我们只会在送这 $K$ 个纪念品时越过了中点，才会走一周。越过一次中点后中点两边的人都给了，所以就不可能再会过中点了。

假设我们会走一周。那么我们就枚举所有穿过中点的 $K$ 个人。答案就是这 $K$ 个人左右做送东西原路返回所需的时间，加上走一圈的时间。如图所示，假设红线为中点，底部为起点。我们枚举每个这样包含 $K$ 个人的蓝色区间让他走一周即可。

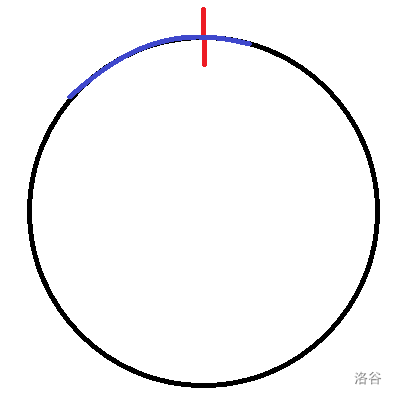
假设我们不会走一周，那就更简单了，直接让中点左右都做送东西原路返回，答案是左右两边加起来。

实现的话可以使用动态规划。设 $dp_i$ 为以第 $i$ 个元素作为送东西原路返回的终点所需的时间。若 $i$ 在左半部分的话转移方程是 $dp_i=p_i+dp_{i-k}$，在右边则是 $dp_i=L-p_i+dp_{i+k}$。注意我们并不关心每个区域有几个人，我们只关心人在哪个区域。

以下是代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,k,l;
int a[10000005];
int dp[10000005];
bool right(int i){
    return a[i]>=(l+1)/2;
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>k>>l;
    for (int i=1;i<=n;i++) cin>>a[i];
    int b;
    for (int i=1;;i++) {
        if (right(i)) {
            b=i;
            break;
        }
        dp[i]=a[i]+dp[max(0ll,i-k)];
    }
    for (int i=n;right(i);i--) dp[i]=l-a[i]+dp[min(n+1,i+k)];
    int ans=21000000000000000;
    for (int i=1;i<=n;i++){
        if (i+k-1<b) continue;
        if (i+k-1>n||i>=b) break;
        ans=min(ans,2*dp[i-1]+2*dp[i+k]+l);
    }
    cout<<min(ans,dp[b-1]*2+dp[b]*2);
    return 0;
}