自动搬运

查看原文

来自洛谷，原作者为

	Stephen_Curry **

搬运于2025-08-24 22:14:40，当前版本为作者最后更新于2019-12-15 21:15:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

时间凑不上，比赛没能打成，发个题解来弥补一下……

第一眼看到样例，突然产生一种瞎猜的想法：是否只要先输出$n$以内的正整数，再输出当中的奇数，最后输出偶数就行了呢？

算了一下，发现这种乱搞解法在$n=5$和$n=7$时同样正确，于是尝试提交一下居然还真过了？

不管怎么凑巧，不管窝运气到底怎么爆棚，这种方法必须要经过证明才可以算得上正解。

于是便有了这篇题解。

证明过程：

啊啊啊一开始把$\large\frac{1}{2}$当成$2$了害得窝算了好久都不对qwq

咱们先设当前计算的为第$k$门科目，$n$为科目总数。

这时的$k$便出现了两种可能的情况：

1. 奇数

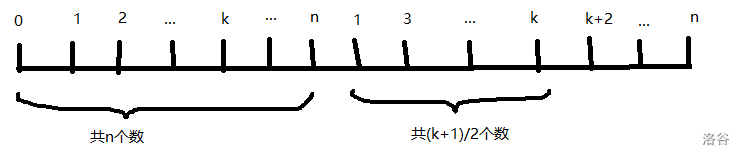
图纯手画真的很丑

显然两个$k$之间的差为

这里要注意坑点：间隔数比两数差少$1$，即此结果仍需减去$1$，即间隔数应为

化简后得

显然易发现，$k$越小，该式结果越大，且每相邻两个奇数代入该式后得到的结果相差$1$，换句话说，在$k$为奇数时，间隔数排序后恰好为一个公差为$1$的等差数列！

2. 偶数

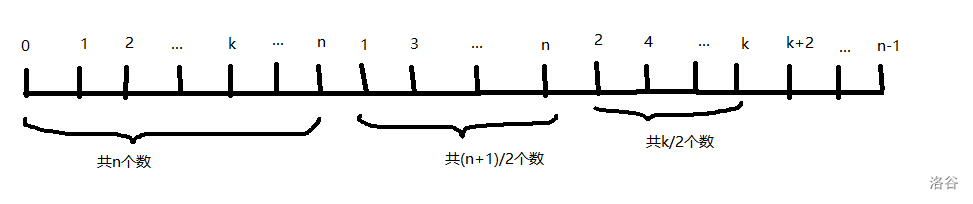
接着上面的无敌丑图继续画，即可得到偶数的间隔：

化简后得

显然结果与奇数一样，在$k$为偶数时，间隔数排序后也恰好为一个公差为$1$的等差数列！

既然奇偶数都为等差数列，咱们就可以看这两个等差数列是否能拼成一个等差数列了。

奇数的间隔数列最小到$n-\large\frac{n+1}{2}=\frac{n-1}{2}$，最大到$n-1$；偶数的间隔数列最小到$\frac{3n\ -\ (n\ -\ 1\ +\ 1)}{2}$ $=n$，最大到$\large\frac{3n-3}{2}$，显然两者可拼接为一个公差为$1$的等差数列。

证明完毕。

有了这个证明，我们即可得出程序：

#include <bits/stdc++.h>
#define rp cout << i << " ";   //懒
using namespace std;
int n;
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)    rp  //输出全数列
    for (int i = 1; i <= n; i += 2) rp  //输出奇数
    for (int i = 2; i < n; i += 2)  rp  //输出偶数
    return 0;  //完结撒花～
}