15011418730 LV 7 @ 2025-8-24 22:14:40

自动搬运

来自洛谷，原作者为

	KesdiaelKen **

搬运于2025-08-24 22:14:40，当前版本为作者最后更新于2019-12-19 15:50:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

~~题面写的好累~~

本题是一道图论+高精题目，这两部分都在本题中占有很重要的地位。

点权和边权都是正的。因为到达的城市都要进行交易，经过的边也都要花费金币，所以我们可以让每条边表示其边权和其指向城市的点权这两个信息。这样，题意就变成了：从图中每个点出发，走任意长度路径，每走过一条边货物会按比例减少一定数值，求走过的所有边边权与货物量的乘积之和。

可以发现本题与幸福路径这题很像（事实上只要会做这道题，原题就是双倍经验）。只不过原题是要输出一个小数，而本题要输出的是分数。原题倍增floyd的做法在本题显然行不通。我们需要一个不利用精度的解法。

考虑从其中一个点出发的情形。显然，路径长度要么有限，要么无限。我们先考虑路径长度无限的情况。

因为路径长度无限，显然至少有一个点被经过无限次。假设这个点是 $i$ ，则路径的情况一定是这样的：从起点走到 $i$ ，然后走过几个经过 $i$ 的环，并一直走下去。然而，只是知道这些，我们并不能很好地做出这题。这个模型需要更多的约束条件。

我们先考虑环的条件。凭感觉似乎能够想出，在所有经过 $i$ 的环中，有一个是最优的。但是该如何证明呢？

因为经过环的数量是无限的，可以考虑类似数学归纳法的方法证明。

我们把经过的环排成一个序列。例如，如果先后经过环 $C_1,C_2,C_3,C_2$ ，则形成的序列就是 $C_1C_2C_3C_2$ 。

考虑这样一个事情：如果有长度为无限的序列 $C_1C_2C_3C_4...$ ，我们希望得到序列 $C_xC_1C_2C_3C_4...$ 。这时候，我们可以考虑在 $C_1C_2C_3C_4...$ 前加上一个 $C_x$ 。

这听起来很简单，但如果我们希望由 $C_1C_2C_3C_4...$ 得到的序列式 $C_aC_bC_cC_d...$ 呢？可以考虑扩展上述思路：先在 $C_1C_2C_3C_4...$ 前加上 $C_aC_bC_cC_d...$ 的尾项（这么说可能不是很严谨，因为一个长度为无穷的序列没有尾项，先大致理解一下意思即可），然后再加上尾项的前一项，一直加到 $C_aC_bC_cC_d...$ 的第一项。此时， $C_aC_bC_cC_d...$ 为新的序列开头的部分。又因为 $C_aC_bC_cC_d...$ 长度为无限，导致原来的 $C_1C_2C_3C_4...$ 对整体的贡献变成了无穷小，不用考虑。这样，我们就把 $C_1C_2C_3C_4...$ 转化为了 $C_aC_bC_cC_d...$ 。

通过上面的思路我们发现，任何一个无穷长的序列都可以由另一个无穷长的序列转化过来。

就着这样的思路，我们来探究一下：对于一个长度为无穷的序列 $\{C_i\}$ ，若在其队首加上环 $B$ ，得到的新序列的值（按照题目从 $i$ 开始走边得到的值）与原序列比较会如何变化。

设 $\{C_i\}$ 的值为 $v_C$ ，单个环 $B$ 的值为 $v_B$ ，其长度（经过的边数）为 $l_B$ 。设 $q=\frac{t}{s+t}$ （每走过一条边货物量的下降程度），则加上 $B$ 形成的新环值为 $v_B+q^{l_B}v_C$ 。将其与 $v_C$ 比较。我们让 $v_C$ 都移到同一边，即 $v_B$ 与 $(1-q^{l_B})v_C$ 比较。因为 $0<q<1$ ，可以变为 $v_B\frac{1}{1-q^{l_B}}$ 与 $v_C$ 比较。对数列比较敏感的同学应该已经看出来了，左式其实就是环序列 $BBBB...$ 的值了。所以，如果 $BBBB...$ 比 $\{C_i\}$ 优，则在 $\{C_i\}$ 前加上 $B$ 形成的序列比 $\{C_i\}$ 优。反之亦然。注意这是个充要条件，即若在 $\{C_i\}$ 前加上 $B$ 形成的序列比 $\{C_i\}$ 优，则 $BBBB...$ 比 $\{C_i\}$ 优。

显然，我们可以构造一个初始序列，让所有序列都由在其队首添加项的方式得来。

所有单环中必有一个是最优的。我们设其为 $A$ ，构造初始序列 $AAAA...$ 。那么，根据上面的原理，可以推得 $AAAA...$ 是所有环序列中最优的。

接下来我们考虑 $A$ 的性质。如果 $A$ 中有重复经过节点，则显然 $A$ 中包含至少两个环。我们把其中值较大的环用上述方式列成初始序列，则 $AAAA...$ 比其小。因此， $A$ 中不会重复经过节点，即 $A$ 的长度不大于 $n$ 。

这样，路径模型的后半部分就解决了。只需解决从起点走到 $i$ 这部分路径的情况。

有了上面解决环问题的经验，我们可以大致得出这部分路径应该具有什么性质：不重复经过任何节点，即不经过环。我们可以这样想，先证明路径上如果仅有一个单环时，其非最优性。接下来，路径上有若干个单环的情况都可以由这部分推得。

若路径上只有一个单环，那么加上之后的环部分，整条航线只会经过两个环（$i\rightarrow j\rightarrow B\rightarrow k\rightarrow AAAA...$）。（如图）)

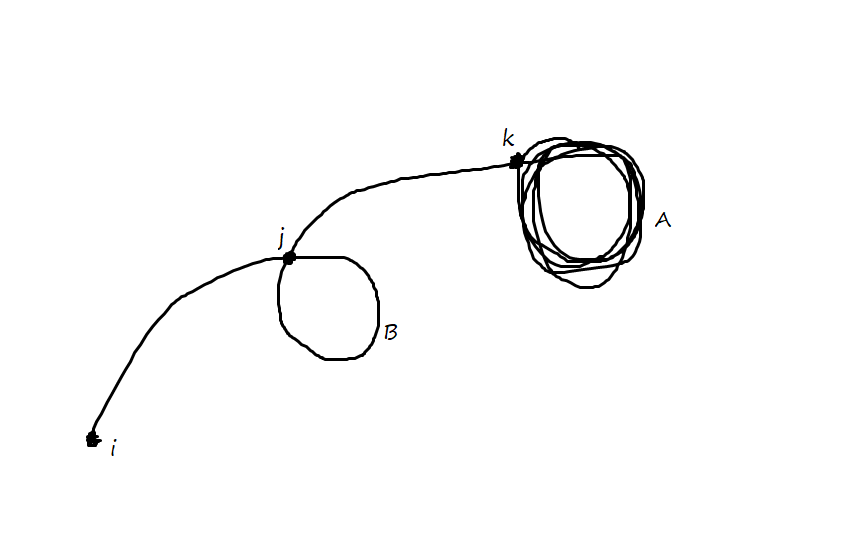这种情况下，有两种符合“路径不重复经过节点”条件的航线： $i\rightarrow j \rightarrow BBBB...$ 和 $i\rightarrow j\rightarrow k \rightarrow AAAA...$ 。我们只需要证明，这两种情况的值至少有一个比$i\rightarrow j\rightarrow B\rightarrow k\rightarrow AAAA...$这种航线大即可。

由于三种路径都经过 $i\rightarrow j$ ，我们大可将这段省去。于是，我们需要比较 $j\rightarrow B\rightarrow k\rightarrow AAAA...$ ， $j \rightarrow BBBB...$ 与 $j\rightarrow k \rightarrow AAAA...$ 。

用 $K$ 表示 $j\rightarrow k$ 这段路程，则 $j\rightarrow B\rightarrow k\rightarrow AAAA...$ 对应的序列为 $BKAAAA...$ ， $j \rightarrow BBBB...$ 对应 $BBBB...$ ， $j\rightarrow k \rightarrow AAAA...$ 对应 $KAAAA...$ 。

考虑先比较 $BKAAAA...$ 与 $KAAAA...$ 。若 $BKAAAA...$ 值小于 $KAAAA...$ 则已经得证；否则，根据上面的结论， $BBBB...$ 值大于 $KAAAA...$ ，而 $BBBB...$ 恰好为 $j \rightarrow BBBB...$ 对应的序列。因此得证。

所以，我们已经得出模型的限制条件了：从 $i$ 出发，经过一个无环路径，然后一直走一个单环。无环路径与单环的长度都不大于 $n$ 。

这就是路径长度为无限的做法。路径长度有限的做法其实只需要参考环之前的部分即可。

于是，我们可以先用 $O(n^2m)$ 递推出从 $i$ 到 $j$ 路径长度为 $k$ 的最大值，然后得到经过每个点的最大环。之后枚举起点与环之前路径的终点，路径长度，得到起点的答案即可。

这样这道题的思路就得出了。接下来就是高精的事情了。

如果用普通的分数高精，则在计算过程中会因为通分而炸掉。考虑先把 $\frac{s}{s+t}$ 的 $s+t$ 乘到分母，在最后再除回来，这样就可以避免以上问题。

然后，还需要注意一下各种优化，包括常数优化和非常数优化，比如递推时如果直接用三维数组空间会炸，要用滚动数组等。

其实这道题的解法很容易想到，但是要证明还是比较困难的。代码难度主要在于高精度，~~上网找板子就可以了~~。

$\%10$

不写高精直接做。

$\%50$

写的很菜的高精。

成环部分

由于只存在一个环，判断一下是否使用即可。

$DAG$ 部分

$DAG$ 上DP。

$\%100$

写的不是那么菜的高精。

下面是参考程序（写的很长且很难看，请见谅）：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<string>
#include<iostream>
using namespace std;
const long long mod=1e9;const int wss=9;
const long long che[9]={1e0,1e1,1e2,1e3,1e4,1e5,1e6,1e7,1e8};
struct GJD
{
    long long num[100];int len;
    GJD(){len=0;}
    inline bool operator<=(GJD&a)
    {
        if(len!=a.len)return len<a.len;
        for(register int i=len-1;i>=0;i--)if(num[i]!=a.num[i])return num[i]<a.num[i];
        return true;
    }
    inline bool operator==(GJD&a)
    {
    	if(len!=a.len)return false;
    	for(register int i=len-1;i>=0;i--)if(num[i]!=a.num[i])return false;
    	return true;
	}
    inline void jia(GJD&a,GJD&b)
    {
        long long x=0;len=0;
        for(;len<a.len||len<b.len||x;len++)
        {
            if(len>=a.len)a.num[len]=0;
            if(len>=b.len)b.num[len]=0;
            num[len]=a.num[len]+b.num[len]+x;
            if(num[len]<mod)x=0;
            else{x=1;num[len]-=mod;}
        }
        while(len>1&&num[len-1]==0)len--;
    }
    inline void jian(GJD&a,GJD&b)
    {
        long long x=0;len=0;
        for(;len<a.len||len<b.len||x;len++)
        {
            if(len>=a.len)a.num[len]=0;
            if(len>=b.len)b.num[len]=0;
            num[len]=a.num[len]-b.num[len]-x;
            if(num[len]>=0)x=0;
            else{x=1;num[len]+=mod;}
        }
        while(len>1&&num[len-1]==0)len--;
    }
    inline void cheng(GJD&a,GJD&b)
    {
        for(register int i=0;i<=a.len+b.len;i++)num[i]=0;
        for(register int i=0;i<a.len;i++)
        {
            if(a.num[i]==0)continue;
            for(register int j=0;j<b.len;j++)
            {
                num[i+j]+=a.num[i]*b.num[j];
                num[i+j+1]+=num[i+j]/mod;
                num[i+j]-=num[i+j]/mod*mod;
            }
        }
        len=a.len+b.len;
        while(len>1&&num[len-1]==0)len--;
    }
    inline GJD operator/(GJD&b)
    {
        GJD a,c,d,e;a.len=len;for(int i=0;i<len;i++)a.num[i]=num[i];
        int ks=d.len=len-b.len+1;
        if(ks<=0)
        {
            d.len=1;d.num[0]=0;
            return d;
        }
        long long zuo,you,mid;
        for(int i=ks;i>=1;i--)
        {
            memset(c.num,0,sizeof(c.num));
            c.len=i;
            zuo=0,you=mod-1;
            while(zuo!=you)
            {
                mid=(zuo+you+1)>>1;
                c.num[i-1]=mid;
                e.cheng(c,b);
                if(e<=a)zuo=mid;
                else you=mid-1;
            }
            c.num[i-1]=d.num[i-1]=zuo;
            e.cheng(c,b);c.jian(a,e);a=c;
        }
        while(d.len>1&&d.num[d.len-1]==0)d.len--;
        return d;
    }
};
inline void output(GJD&a)
{
    printf("%lld",a.num[a.len-1]);
    for(int i=a.len-2;i>=0;i--)
    {
        for(int j=wss-1;j>=0;j--)
        {
            if(a.num[i]>=che[j])
            {
                printf("%lld",a.num[i]);
                break;
            }
            printf("0");
        }
    }
}
GJD gjd,gjdgjd;
GJD gcd(GJD x,GJD y)
{
    if(y.num[0]==0&&y.len==1)return x;
    gjd=x/y;gjdgjd.cheng(gjd,y);gjd.jian(x,gjdgjd);
    return gcd(y,gjd);
}
struct BIGNUM
{
	GJD shu;bool zf;
	BIGNUM(){zf=true;}
	inline bool operator<(BIGNUM&a)
	{
		if(!zf&&a.zf)return true;
        if(zf&&(!a.zf))return false;
        if(shu==a.shu)return false;
        return (shu<=a.shu)^(!zf);
	}
	inline void jia(BIGNUM&a,BIGNUM&b)
	{
		if(a.zf==b.zf)
		{
			zf=a.zf,shu.jia(a.shu,b.shu);
			return;
		}
		if(a.zf)
		{
			if(b.shu<=a.shu)zf=true,shu.jian(a.shu,b.shu);
			else zf=false,shu.jian(b.shu,a.shu);
		}
		else
		{
			if(a.shu<=b.shu)zf=true,shu.jian(b.shu,a.shu);
			else zf=false,shu.jian(a.shu,b.shu);
		}
	}
	inline void jian(BIGNUM&a,BIGNUM&b)
	{
		if(a.zf==!b.zf)
		{
			zf=a.zf,shu.jia(a.shu,b.shu);
			return;
		}
		if(a.zf)
		{
			if(b.shu<=a.shu)zf=true,shu.jian(a.shu,b.shu);
			else zf=false,shu.jian(b.shu,a.shu);
		}
		else
		{
			if(a.shu<=b.shu)zf=true,shu.jian(b.shu,a.shu);
			else zf=false,shu.jian(a.shu,b.shu);
		}
	}
	inline void cheng(BIGNUM&a,BIGNUM&b)
	{
		shu.cheng(a.shu,b.shu);
		zf=!(a.zf^b.zf);
	}
};
GJD aa,bb;
struct FRAC
{
    GJD fz,fm;bool zf;
    FRAC(){zf=true;}
    inline void operator=(BIGNUM&a)
	{
		zf=a.zf;
		fz=a.shu;
		fm.len=1;fm.num[0]=1;
	}
    inline bool operator<(FRAC&a)
    {
        if(!zf&&a.zf)return true;
        if(zf&&(!a.zf))return false;
        GJD aa,bb;aa.cheng(fz,a.fm),bb.cheng(fm,a.fz);
        if(aa==bb)return false;
        return (aa<=bb)^(!zf);
    }
    inline bool operator<(BIGNUM&a)
    {
    	if(!zf&&a.zf)return true;
        if(zf&&(!a.zf))return false;
        GJD aa=fz,bb;bb.cheng(fm,a.shu);
        if(aa==bb)return false;
        return (aa<=bb)^(!zf);
	}
    inline void jia(FRAC&a,FRAC&b)
    {
        aa.cheng(a.fz,b.fm);bb.cheng(a.fm,b.fz);
        fm.cheng(a.fm,b.fm);
        if(a.zf==b.zf)
		{
			zf=a.zf,fz.jia(aa,bb);
			return;
		}
		if(a.zf)
		{
			if(bb<=aa)zf=true,fz.jian(aa,bb);
			else zf=false,fz.jian(bb,aa);
		}
		else
		{
			if(aa<=bb)zf=true,fz.jian(bb,aa);
			else zf=false,fz.jian(aa,bb);
		}
    }
    inline void jiajia(BIGNUM&a,FRAC&b)
    {
    	aa.cheng(a.shu,b.fm);bb=b.fz;
        fm=b.fm;
        if(a.zf==b.zf)
		{
			zf=a.zf,fz.jia(aa,bb);
			return;
		}
		if(a.zf)
		{
			if(bb<=aa)zf=true,fz.jian(aa,bb);
			else zf=false,fz.jian(bb,aa);
		}
		else
		{
			if(aa<=bb)zf=true,fz.jian(bb,aa);
			else zf=false,fz.jian(aa,bb);
		}
	}
    inline void jian(FRAC&a,FRAC&b)
    {
        aa.cheng(a.fz,b.fm);bb.cheng(a.fm,b.fz);
        fm.cheng(a.fm,b.fm);
        if(a.zf==!b.zf)
		{
			zf=a.zf,fz.jia(aa,bb);
			return;
		}
		if(a.zf)
		{
			if(bb<=aa)zf=true,fz.jian(aa,bb);
			else zf=false,fz.jian(bb,aa);
		}
		else
		{
			if(aa<=bb)zf=true,fz.jian(bb,aa);
			else zf=false,fz.jian(aa,bb);
		}
    }
    inline void cheng(FRAC&a,FRAC&b)
    {
        zf=!(a.zf^b.zf);
		fz.cheng(a.fz,b.fz),fm.cheng(a.fm,b.fm);
    }
}q,std1,std0;
int n,m,fa,fb;
inline void dy(int&a)
{
	int ch=0;a=0;
	while(ch<'0'||ch>'9'){ch=getchar();}
	while(ch>='0'&&ch<='9'){a=a*10+ch-'0';ch=getchar();}
}
inline void dr(BIGNUM&aa)
{
    int a;dy(a);
    aa.zf=true;
    aa.shu.len=1;aa.shu.num[0]=a;
}
inline void fracdr(FRAC&aa)
{
    int a;dy(a);
    aa.zf=true;
    aa.fz.len=aa.fm.len=1;
    aa.fz.num[0]=a,aa.fm.num[0]=1;
}
inline void sc(FRAC aa)
{
    GJD lr=gcd(aa.fz,aa.fm);
    aa.fz=aa.fz/lr,aa.fm=aa.fm/lr;
    output(aa.fz);
    if(aa.fm.len==1&&aa.fm.num[0]==1)return;
    printf("/");output(aa.fm);
}
const int SZ=51;
BIGNUM pn1[100],pn2[100],pn[100],dis[SZ][SZ][2],lsc[SZ][SZ],jl[SZ][SZ],mea[100];
FRAC maxcir[100],pnn[100],ans[100],lc[SZ][SZ];
bool exdis[SZ][SZ][SZ]={0},excir[100]={0},con[SZ][SZ];
int gd;
int main()
{
//  freopen("9.in","r",stdin);
//  freopen("9.out","w",stdout);
    std1.zf=true;std1.fz.len=std1.fm.len=1;std1.fz.num[0]=std1.fm.num[0]=1;
    std0.zf=true;std0.fz.len=std0.fm.len=1;std0.fz.num[0]=0;std0.fm.num[0]=1;
    scanf("%d%d%d%d",&n,&m,&fa,&fb);fracdr(q);
    for(int i=1;i<=n;i++)dr(mea[i]);
    BIGNUM syfm,sy1,sy2;
    syfm.zf=sy1.zf=sy2.zf=true;
    syfm.shu.len=sy1.shu.len=sy2.shu.len=1;
    syfm.shu.num[0]=fa+fb;sy1.shu.num[0]=fa;sy2.shu.num[0]=fb;
    int a,b;BIGNUM c,d,e;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&a,&b);dr(c);
        d.cheng(mea[b],sy1);e.cheng(c,syfm);
        c.jian(d,e);
        if(!con[a][b])jl[a][b]=c;
        else if(jl[a][b]<c)jl[a][b]=c;
        con[a][b]=true;
    }
    pn1[0].shu=std1.fz;pn1[0].zf=true;for(int i=1;i<=n;i++)pn1[i].cheng(pn1[i-1],sy2);
    pn2[n].shu=std1.fz;pn2[n].zf=true;for(int i=n-1;i>=0;i--)pn2[i].cheng(pn2[i+1],syfm);
    for(int i=1;i<=n;i++)pn[i].cheng(pn1[i],pn2[i+1]);
	for(int i=0;i<=n;i++)pnn[i].zf=true,pnn[i].fz=pn1[i].shu,pnn[i].fm=pn2[n-i].shu;
    memset(exdis,0,sizeof(exdis));
    for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
        if(con[i][j])dis[i][j][1].cheng(jl[i][j],pn2[1]),exdis[i][j][1]=true;
    gd=0;
    FRAC f,g;
    for(int i=1;i<=n;i++)
    {
    	if(!exdis[i][i][1])continue;
    	f.jian(std1,pnn[1]);
    	g.zf=!(dis[i][i][1].zf^f.zf);
    	g.fz.cheng(dis[i][i][1].shu,f.fm);
    	g.fm=f.fz;
        if(!excir[i])maxcir[i]=g;
    	else if(maxcir[i]<g)maxcir[i]=g;
        excir[i]=true;
	}
    for(register int i=2;i<=n;i++)
    {
        for(register int k=1;k<=n;k++)
        {
            for(register int s=1;s<=n;s++)
            {
                if(!con[k][s])continue;
                lsc[k][s].cheng(jl[k][s],pn[i-1]);
                for(register int j=1;j<=n;j++)
                {
                    if(!exdis[j][k][i-1])continue;
                    c.jia(dis[j][k][gd^1],lsc[k][s]);
                    if(!exdis[j][s][i])dis[j][s][gd]=c;
                    else if(dis[j][s][gd]<c)dis[j][s][gd]=c;
                    exdis[j][s][i]=true;
                }
            }
        }
        for(int j=1;j<=n;j++)
        {
        	if(!exdis[j][j][i])continue;
    		f.jian(std1,pnn[i]);
    		g.zf=!(dis[j][j][gd].zf^f.zf);
    		g.fz.cheng(dis[j][j][gd].shu,f.fm);
    		g.fm=f.fz;
            if(!excir[j])maxcir[j]=g;
            else if(maxcir[j]<g)maxcir[j]=g;
            excir[j]=true;
		}
        gd^=1;
    }
    for(int j=1;j<=n;j++)
    {
    	if(!excir[j])continue;
    	for(int k=1;k<=n;k++)
    		lc[j][k].cheng(maxcir[j],pnn[k]);
	}
	for(int i=1;i<=n;i++)ans[i]=std0;
	memset(exdis,0,sizeof(exdis));
    for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
        if(con[i][j])dis[i][j][1].cheng(jl[i][j],pn2[1]),exdis[i][j][1]=true;
    gd=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(!exdis[i][j][1])continue;
            if(ans[i]<dis[i][j][1])ans[i]=dis[i][j][1];
            if(!excir[j])continue;
            f.jiajia(dis[i][j][1],lc[j][1]);
            if(ans[i]<f)ans[i]=f;
        }
    }
    for(register int i=2;i<=n;i++)
    {
        for(register int k=1;k<=n;k++)
        {
            for(register int s=1;s<=n;s++)
            {
                if(!con[k][s])continue;
                lsc[k][s].cheng(jl[k][s],pn[i-1]);
                for(register int j=1;j<=n;j++)
                {
                    if(!exdis[j][k][i-1])continue;
                    c.jia(dis[j][k][gd^1],lsc[k][s]);
                    if(!exdis[j][s][i])dis[j][s][gd]=c;
                    else if(dis[j][s][gd]<c)dis[j][s][gd]=c;
                    exdis[j][s][i]=true;
                }
            }
        }
        for(register int j=1;j<=n;j++)
    	{
    	    for(register int k=1;k<=n;k++)
    	    {
    	        if(!exdis[j][k][i])continue;
    	        if(ans[j]<dis[j][k][gd])ans[j]=dis[j][k][gd];
    	        if(!excir[k])continue;
    	        f.jiajia(dis[j][k][gd],lc[k][i]);
    	        if(ans[j]<f)ans[j]=f;
    	    }
    	}
        gd^=1;
    }
    FRAC s1,s2;s1=sy1;s2=sy2;
    s1.fm=s2.fm=syfm.shu;
    for(int i=1;i<=n;i++)
    {
    	d.shu.cheng(ans[i].fm,pn2[0].shu);
        ans[i].fm=d.shu;
        g=mea[i];f.cheng(s1,g);
        g.cheng(s2,ans[i]);
        ans[i].jia(f,g);
        f.cheng(q,ans[i]);
        sc(f);
        printf("\n");
    }
    return 0;
}

ID

4610

时间

2000ms

内存

32MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

$\%10$

$\%50$

成环部分

$DAG$ 部分

$\%100$

【L&K R-03】大航海时代

信息

1 条题解

自动搬运

以下是正文

%10\%10%10

%50\%50%50

成环部分

DAGDAGDAG部分

%100\%100%100

【L&K R-03】大航海时代

信息

还没有账户？

登录

$\%10$

$\%50$

$DAG$ 部分

$\%100$