自动搬运

查看原文

来自洛谷，原作者为

	Azuree What really matters is always very simple.

搬运于2025-08-24 22:14:37，当前版本为作者最后更新于2020-08-03 18:52:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

根据题意，我们可以把位于同一行且左右相邻的点连成一条横边，把位于同一列且上下相邻的点连成一条竖边（这里的“相邻”指的是两个点在横向或竖向上之间没有输入给出的黑点，一个点可以参与多条边）。

比如，我们可以把一个图连成这样：

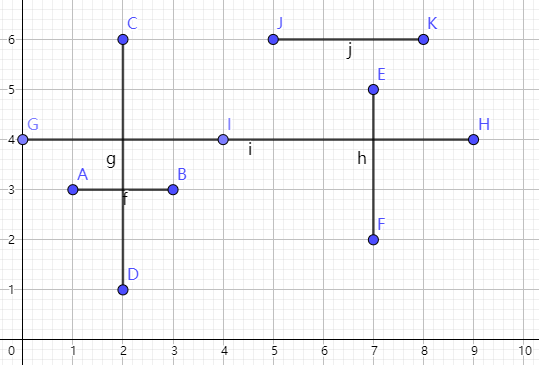
那么，不难发现，能够变成黑点的白点都是位于线段交点上的点。

那么，如何去统计线段交点呢？

我们可以把可以把边分成两类：横向边（和x轴平行的边）和纵向边（和y轴平行的边）。于是，统计交点就等同于每条横向边于纵向 边交点个数的和。而对于这个和，我们可以用扫描线的方法求得。

大体思路是这样的：

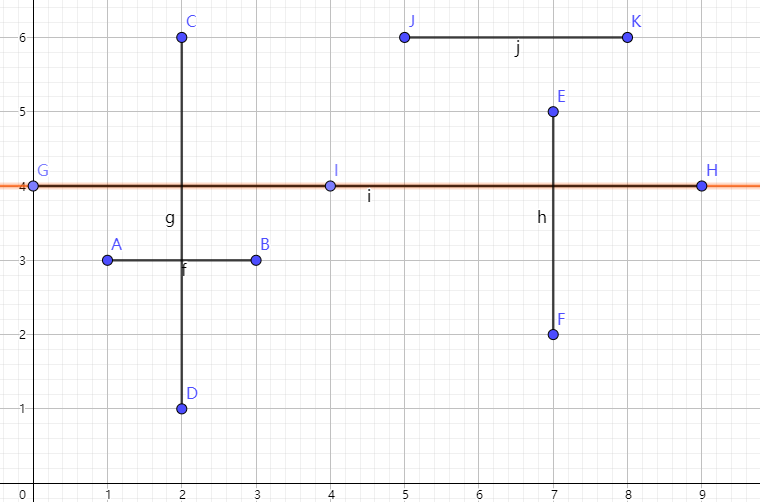
如果扫描线是从上到下进行扫描的，则我们可以用线段树树状数组来记录有多少条纵向边经过了$y=k$。

为了方便理解，我们可以先用一个最普通的数组$t_{1,9}$来记录纵边经过点$y=k$的距离。如下图，若我们以$y=4$为例，则$t_{1,9}=0,1,0,0,0,0,1,0,0$，其中两个$1$表示的便是两个交点。而对于查询，交点数量便是线段GI、线段IH上交点数量的和。我们发现，如果直接在刚刚的数组$t_{1,9}$中统计，那么复杂度为$O(n)$。我们可以用树状数组来优化这一步，来完成这个本质上是区间求和的工作。

对于树状数组的修改，我们只需在纵边的第一个点被扫到时在数组的对应位置加一，在纵边的第二个点被扫到后在对应位置减一即可。

code:

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<algorithm>
#define ll long long
#define INF 0x7fffffff
#define qwq printf("qwq\n");

using namespace std;

int read() {
    register int x = 0,f = 1;register char ch;
    ch = getchar();
    while(ch > '9' || ch < '0'){if(ch == '-') f = -f;ch = getchar();}
    while(ch <= '9' && ch >= '0'){x = x * 10 + ch - 48;ch = getchar();}
    return x * f;
}

struct node {
	int x, y;
}u[400005];

struct edge {
	int up, down, left, right;
}e[400005];

struct edge_end {
	int x, y;
	bool operator < (const edge_end &a) const {return a.y < y;}
};

int n, m, cnt, ans, maxx, a[400005], t[400005];

priority_queue<edge_end> que;

void Read_in() {
	n = read();
	for(int i = 1; i <= n; i++) {
		u[i].x = read(); u[i].y = read();
		a[++cnt] = u[i].x; a[++cnt] = u[i].y;
	}
}

void Discretization() {
	sort(a + 1, a + cnt + 1);
	cnt = unique(a + 1, a + cnt + 1) - a - 1;
	for(int i = 1; i <= n; i++) {
		u[i].x = lower_bound(a + 1, a + cnt + 1, u[i].x) - a;
		u[i].y = lower_bound(a + 1, a + cnt + 1, u[i].y) - a;
		maxx = max(maxx, u[i].x);
	}
}

bool xsort(node a, node b) {return a.x == b.x ? a.y < b.y : a.x < b.x;}
bool ysort(node a, node b) {return a.y == b.y ? a.x < b.x : a.y < b.y;}
bool esort(edge a, edge b) {return a.up == b.up ? a.left < b.left : a.up < b.up;}

void Make_edge() {
	sort(u + 1, u + n + 1, xsort);    // x 相同    处理竖边 
	for(int i = 1; i < n; i++) {
		if(u[i + 1].x != u[i].x || u[i + 1].y - u[i].y < 2) continue;
		e[++m].up = u[i].y + 1; e[m].down = u[i + 1].y - 1; e[m].right = u[i].x;
	}
	sort(u + 1, u + n + 1, ysort);    // y 相同    处理横边 
	for(int i = 1; i < n; i++) {
		if(u[i + 1].y != u[i].y || u[i + 1].x - u[i].x < 2) continue;
		e[++m].up = u[i].y; e[m].left = u[i].x + 1; e[m].right = u[i + 1].x - 1;
	}
	sort(e + 1, e + m + 1, esort);
}

int lowbit(int x) {return x & -x;}
void update(int x, int k) {while(x <= maxx) {t[x] = t[x] + k; x = x + lowbit(x);}}
int query(int x) {int ans = 0; while(x) {ans = ans + t[x]; x = x - lowbit(x);} return ans;}

void Scanning() {
	for(int i = 1; i <= m; i++) {
		int deep = e[i].up;
		while(!que.empty() && que.top().y <= deep) {update(que.top().x, -1); que.pop();}
		if(!e[i].left) {update(e[i].right, 1); que.push((edge_end){e[i].right, e[i].down + 1});}
		else {ans = ans + query(e[i].right) - query(e[i].left - 1);}
	}
}

void Print() {printf("%d\n", ans + n);}

int main() {
	Read_in();
	Discretization();
	Make_edge();
	Scanning();
	Print();
    return 0;
}