1 条题解
-
0
自动搬运
来自洛谷,原作者为

chen_03
AFO | 垫底人,啥都不会 | 谁能赐予我一个脑子? | Brute force 出不了奇迹。搬运于
2025-08-24 22:14:35,当前版本为作者最后更新于2022-08-31 16:55:37,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
吐槽:我在网上能找到的所有题解,要么对关键性质的阐述过于简洁,让我这个低水平选手看得云里雾里;要么推广关键性质时的说明过少,或是给出了对想出正解毫无帮助的部分分性质,让题解有失严谨性与逻辑性。
题目想让我们找一条最短路径。虽然这张图是平面图,但最短路径不免错综复杂,所以我们先确定基本思路:建图跑 Dijkstra 最短路。
原图的点数可以达到 级别,直接跑肯定是不行的,我们考虑简化这张图。
我们先考虑一种特殊情况:不存在一座天桥 ,满足 或 (注意全部是严格小于)。也就是说,任意一座天桥的横坐标范围既不 “横跨” 起点(的横坐标),也不 “横跨” 终点(的横坐标)。
在这种情况下,我们有一个关键性质:
性质 存在一条最优路径,满足:若我们自下而上地进入一座天桥,或自上而下地离开一座天桥,那么进入点(或离开点)一定是这座天桥的某个端点。
注 1 “进入” 表示我们之前不在这座天桥上,现在在这座天桥上;“离开” 表示我们之前在这座天桥上,现在不在这座天桥上。不在这座天桥上时,我们可能在某栋建筑上上下移动,也可能在另一座天桥上左右移动。
注 2 “自下而上地进入” 表示我们进入这座天桥之前,我们在某栋建筑上向上移动;“自上而下地离开” 表示我们离开这座天桥之后,我们在某栋建筑上向下移动。
注 3 进入点与离开点都一定在某栋建筑上。注 4 即使路径与这座天桥只有一个交点(公共点),我们也认为这条路径 “进入” 与 “离开” 了这座天桥各一次。
我们先证明其中一种情况。假设现在有一条最优路径,它自下而上地进入了一座天桥 。天桥 满足 (这里是小于等于,也就是天桥 位于起点右方),且进入点不是天桥 的端点。
有三种情况:进入天桥 之后,离开天桥 之前,我们
- 向左移动了一段距离(图 );
- 向右移动了一段距离(图 );
- 没有左右移动(图 )。
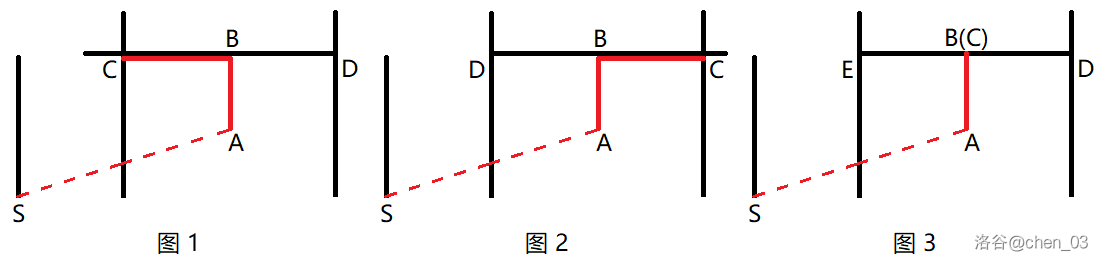
以图 的情况为例。如图, 为起点, 为进入天桥 前向上移动的那一段, 为在天桥 上的移动, 为天桥 的右端点。 不是天桥 的端点, 不一定是天桥 的端点。明确 ,,。
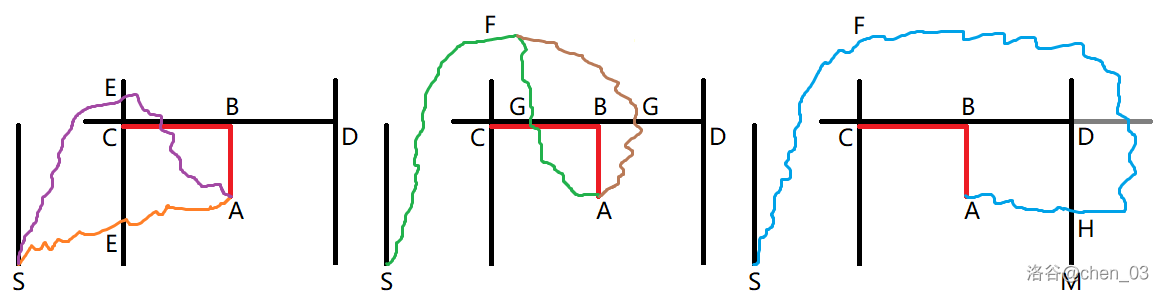
若路径 经过了点 所在的建筑 ,不妨设 最后一次位于建筑 上时在点 上,则 的长度严格小于 的长度(因为 ),替换一下一定更优。这与 “这条路径是最优路径” 矛盾。
那么 没有经过建筑 。设 最后一次位于横坐标 上时在点 上,那么 的过程中横坐标始终 。
若 经过了线段 ,不妨设 最后一次位于线段 上时在点 上,由 得 的长度严格小于 的长度,同样推出矛盾。
那么 经过了线段 的延长线。设点 为点 所在的建筑的底端,由前文可得 经过了线段 。
设 最后一次位于线段 上时在点 上,那么 的长度小于等于 的长度,要么推出矛盾,要么可以把 调整为 而总长度不变。
我们发现 是天桥 的端点。也就是说,我们可以把路径调整为:自下而上地从天桥 的端点 进入天桥 。
对于图 的情况,证明与此类似。图 可以调整为从端点 进入天桥 ,图 可以调整为从端点 或端点 进入天桥 。
UPD 这里我想复杂了。考虑天桥与它两端点所在的建筑构成了 “冂” 形,而起点没有被 “冂” 形包住,所以路径必然经过了 “冂” 形,只要讨论路径最后一次位于 “冂” 形上时在三条线段中的哪一条上即可。
两种证法本质相同,但这种显然更简洁。同理,若天桥 满足 (即天桥 位于起点左方),也可以类似地调整。对于 “自上而下地离开” 的情况,讨论天桥 与终点 的位置关系,用对称的方法证明即可。
到这里我们已经证明了,对于一座特定的天桥 ,我们可以把路径调整为(对天桥 而言)满足关键性质的状态。考虑对于一条最优路径不断地(每次选择一座天桥)进行这样的调整,若调整能在有限次内结束则性质得证。
由前文的证明可得,一次调整的过程一定形如下图:若对于天桥 进行调整,我们只会改变高度不高于天桥 的一段路径。所以我们每次选择最高的不合法的天桥调整即可,这样每座天桥最多被调整一次。于是性质得证。
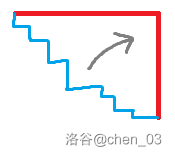
上文中我们讨论的都是 “不存在一座天桥 满足 或 ” 的情况。对于一般情况,我们尝试进行一些调整,使之符合条件。
若天桥 满足 ,我们找到与天桥 有交的:横坐标最大的满足 的建筑 ,和横坐标最小的满足 的建筑 。我们把天桥 拆成三段:,,。前两段都没有 “横跨” 起点 ;对于第三段,可以发现它只与建筑 有交,也就是只能通过两个端点进入与离开这座天桥,所以它不可能产生违背关键性质的情况。
对于 的情况,可以类似地进行拆分。不断地进行这样的拆分即可,天桥的总数仍为 级别。
有了这个关键性质,我们就可以对原图进行简化了。假设我们从天桥 出发向下走到天桥 (没有拐弯,下同),或从天桥 出发向上走到天桥 ,不难发现,这一过程中经过的所有位于某座天桥上的点,除天桥 上的那个点以外,都一定是某座天桥的端点。因此除起点和终点外,我们只需保留所有天桥的端点,以及每个端点下方第一个位于某座天桥上的点即可。
这样点数和边数都被缩减到了 级别。时间复杂度一个 。
如果要问这个关键性质是怎么想到的,按我的理解,大概是对着 , 的部分分画画图找找规律,再推广到一般情况吧。
代码写得很丑,仅供参考。
#include <bits/stdc++.h> #define eb emplace_back #define ls u<<1 #define rs u<<1|1 #define fi first #define se second using namespace std; typedef long long ll; typedef pair<int,int> pii; typedef pair<ll,int> pli; int n,m,M,S,G,t=1,L,R,x[100005],h[100005],p[100005]; int l[100005],r[100005],y[100005],z[100005]; int ti[400005],a[200015],b[200015],cnt,bg,ed,tot; vector<pii> vec[100005],e[1200005]; set<int> s; set<int>::iterator it; map<int,int> mp[100005]; priority_queue<pli,vector<pli>,greater<pli> > q; ll dis[1200005]; inline pii calc(int x,pii u,vector<pii> &V){ it=s.lower_bound(x),R=*it; L=*(R^x?--it:it); V.eb(pii(u.fi,L)),V.eb(pii(R,u.se)); u.fi=L,u.se=R; return u; } void cover(int u,int l,int r,int x,int y,int z){ if(x<=l && r<=y)return ti[u]=z,void(); int mid=(l+r)>>1; if(x<=mid)cover(ls,l,mid,x,y,z); if(y>mid)cover(rs,mid+1,r,x,y,z); } int que(int u,int l,int r,int x){ if(l==r)return ti[u]; int mid=(l+r)>>1; if(x<=mid)return max(ti[u],que(ls,l,mid,x)); return max(ti[u],que(rs,mid+1,r,x)); } inline int id(int x,int y){ if(mp[y].count(x))return mp[y][x]; return mp[y][x]=++tot; } inline void ins(int u,int v,int w){ e[u].eb(pii(v,w)); e[v].eb(pii(u,w)); } inline void work(int k){ cnt=0; for(auto u:vec[k]) a[++cnt]=u.fi,a[++cnt]=u.se; sort(a+1,a+1+cnt); cnt=unique(a+1,a+1+cnt)-a-1; for(int i=1,u,v;i<=cnt;++i){ u=id(a[i],k); if((v=que(1,1,n,a[i]))==-1)continue; ins(u,id(a[i],v),z[k]-z[v]); } for(auto u:vec[k]) cover(1,1,n,u.fi,u.se,k); } inline void work2(int k){ cnt=0,t=1; for(auto u:mp[k]) a[++cnt]=u.fi,b[cnt]=u.se; sort(vec[k].begin(),vec[k].end()); for(auto u:vec[k]){ while(t<=cnt && a[t]<u.fi)++t; while(t<cnt && a[t+1]<=u.se) ins(b[t],b[t+1],x[a[t+1]]-x[a[t]]),++t; } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;++i){ scanf("%d%d",x+i,h+i); s.insert(i),p[i]=i; } sort(p+1,p+1+n,[](int X,int Y){ return h[X]<h[Y]; }); for(int i=1;i<=m;++i){ scanf("%d%d%d",l+i,r+i,y+i); ++l[i],++r[i],z[i]=y[i]; } sort(z+1,z+1+m); M=unique(z+1,z+1+m)-z-1; for(int i=1;i<=m;++i){ y[i]=lower_bound(z+1,z+1+M,y[i])-z; vec[y[i]].eb(l[i],r[i]); } scanf("%d%d",&S,&G),++S,++G; if(S>G)swap(S,G); for(int i=1;i<=n*4;++i)ti[i]=-1; bg=id(S,0),cover(1,1,n,S,S,0); ed=id(G,0),cover(1,1,n,G,G,0); for(int k=1;k<=M;++k){ while(t<=n && h[p[t]]<z[k])s.erase(p[t++]); for(int i=0;i<(int)vec[k].size();++i){ pii u=vec[k][i]; if(u.fi<S && S<u.se) vec[k][i]=calc(S,u,vec[k]); else if(u.fi<G && G<u.se) vec[k][i]=calc(G,u,vec[k]); } work(k); } for(int i=1;i<=M;++i)work2(i); for(int i=1;i<=tot;++i)dis[i]=2e18; dis[bg]=0,q.push(pli(0,bg)); while(!q.empty()){ pli t=q.top();q.pop(); int u=t.se; if(dis[u]<t.fi)continue; dis[u]=t.fi; for(auto v:e[u]){ if(dis[v.fi]<=dis[u]+v.se)continue; dis[v.fi]=dis[u]+v.se; q.push(pli(dis[v.fi],v.fi)); } } printf("%lld\n",dis[ed]<1e18?dis[ed]:-1); return 0; }
- 1
信息
- ID
- 4821
- 时间
- 2500~4000ms
- 内存
- 1000MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
