自动搬运

查看原文

来自洛谷，原作者为

	Stay_Hungry 这个家伙很菜，什么也没有留下

搬运于2025-08-24 22:14:22，当前版本为作者最后更新于2020-01-14 11:42:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

从0.1开始的斜率优化（dalao请跳过，不喜误喷）

---

因为我是真的菜，写不来逼格高的，只得写篇详细而通俗易懂的题解。

那么何为“斜率优化”呢？
答曰：用线性规划优化dp式。

如果不会线性规划，问题也不大，接下来开始题解正文部分：

以下正文部分分成3类数据题解。

$$1.(1\le n\le5000,1\le t_i,c_i\le100)$$

其实我个人感觉$O(n^3)dp$很难想=-=

按照题意来，我们设$f_i$表示完成到以第$i$个任务为结束任务时所花费的最短时间

外层枚举$i$，内层枚举$j$，表示从$j+1$到$i$这一段任务加入到$f_j$所表示的任务安排区间，然后加上贡献取$min$即可。

对于开机时间，只会对开机一次后的任务产生影响，所以直接加上$S*(c_{j+1}+...+c_{n})$，对于这段任务的完成费用，直接前缀和$T_i$乘一下即可

所以我们可以得出dp式：

$$f_i=Min_{0\le j<i}(f_j+S*c(j,n)+t_i*c(j,i))$$ $$c(a,b)=\sum^{i=a+1}_{i\le b} c_i$$

然后用前缀和维护$c(a,b)$，这样就愉快的切掉弱化版P2365。

$$f_i=f_j+S*(sc_n-sc_j)+st_i*(sc_i-sc_j)$$

分析复杂度：内外两层循环，时间复杂度为$O(n^2)$，是肯定不行的，然后此时我们就得用斜率优化来优化时间复杂度。

我们把$Min$去除，然后化简，用其他元素表示$f_j$

$$f_i=f_j+S*(sc_n-sc_j)+st_i*(sc_i-sc_j)$$ $$f_i=f_j+S*sc_n-S*sc_j+st_i*sc_i-st_i*sc_j$$ $$f_j=(S+sc_i)sc_j+f_i-S*sc_n-st_i*sc_i$$ $$y=f_j$$ $$k=(S+sc_i)$$ $$x=sc_j$$ $$b=f_i-S*sc_n-st_i*sc_i$$

这样我们就可以得到一个一次函数解析式。

然而为啥要这么分呢？
答曰：把外循环时可以不能直接得出的放在$x$或$y$处，$k$和$b$都是可以依靠外指针$i$得到的，然后就可以开始愉快的斜率优化啦！

对于选择不同的$j$更新$f_i$的值，我们把$j$称为决策点，对于任意一个决策点，我们都能把它表示在以$sc_j$为$x$轴，以$f_j$为$y$轴的平面直角坐标系上。

对于一个决策点所对应的直线，都可以解出一段截距$b$，而

$b=f_i-S*sc_n-st_i*sc_i$中$-S*sc_n-st_i*sc_i$是可以直接得到固定值的，因此$b$越大，$f_i$越大。

$2.(1\le n\le 3*10^5,1\le c_i , t_i \le 10^4)$
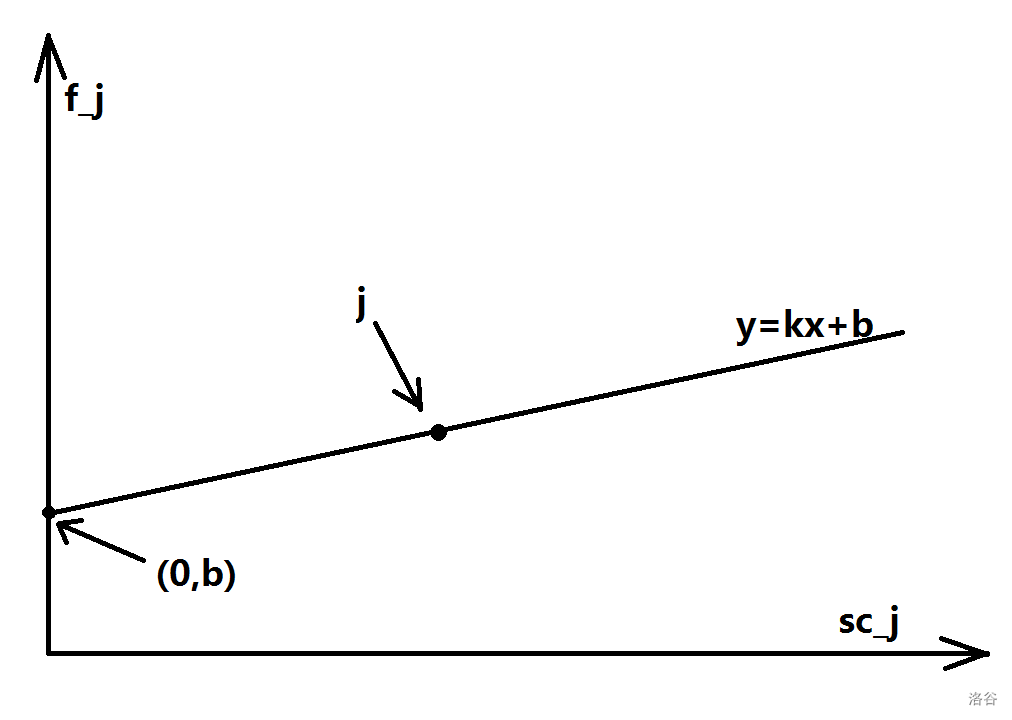
了解大致原理后，我们需先分析单调性。
当$j$单调递增时，$c_i>0$，因此$sc_j$单调递增，且$t_i>0$，因此$f_i$单调递增，$k$单调递增。

接下来我们就需考虑最优决策点的选择。
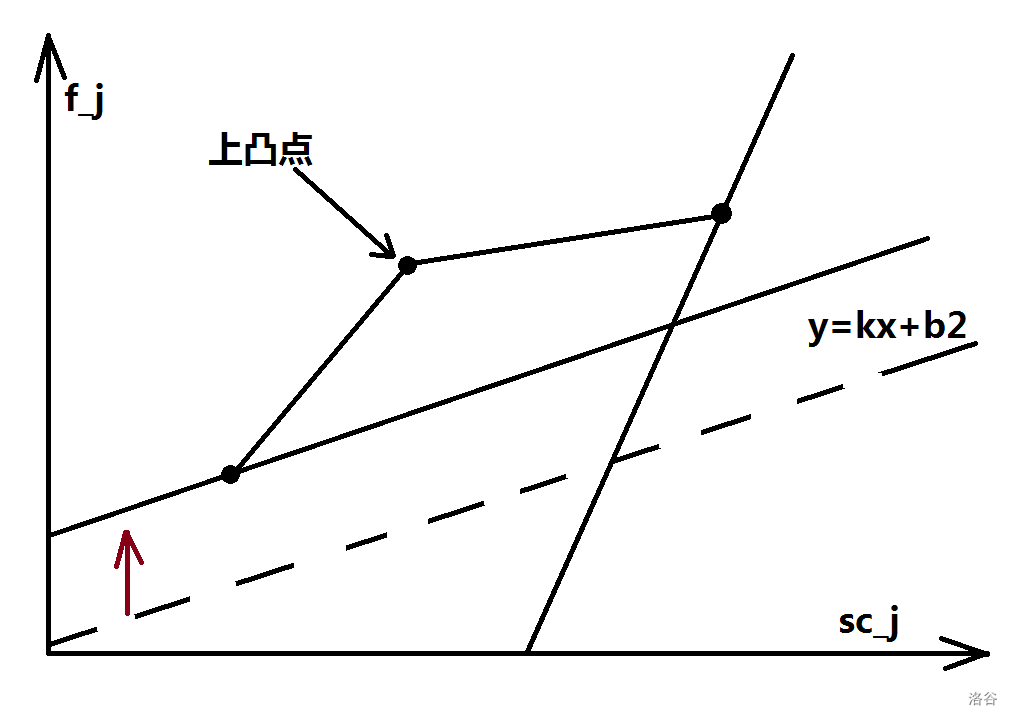
通俗一点讲，所谓选择最优决策点就是把一条斜率为$s+sc_i$的直线从下向上靠，第一个相交的点就是最优决策点（因为此时$b$最小，$f_i$也必定最小）。

而对于上凸点，无论直线的斜率怎么变化，最先相交的点必定不是上凸点，因此我们可以将所有上凸点都移出决策点队列，最后，我们可以得到一个下凸包。

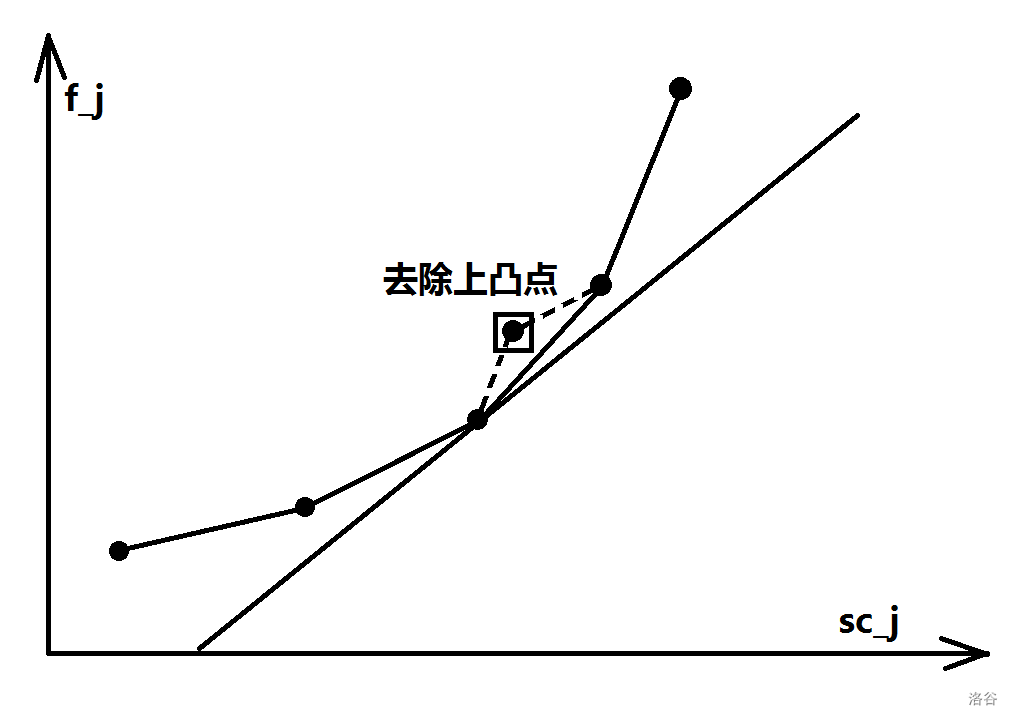
因此对于任意决策点$a$,$b$,$c$ $(a<b<c)$，满足$k_a<k_b<k_c$，即决策点斜率单调递增。
因为$k$单调递增，因此小于当前$k(k=s+sc_i)$决策点可以移出决策点队列。

分析时间复杂度：每个点进出队列1次，时间复杂度$O(n)$。

$3.(1\le n\le3*10^5,0\le c_i\le2^8,-2^8\le t_i\le2^8)$

此时$t_i$可能为负数，因此$f_j$不一定单调递增，所以决策点连线的直线可能为负数，决策时$k$也可能为负数。

同样，上凸点一定不是最优决策点，因此需维护下凸包。

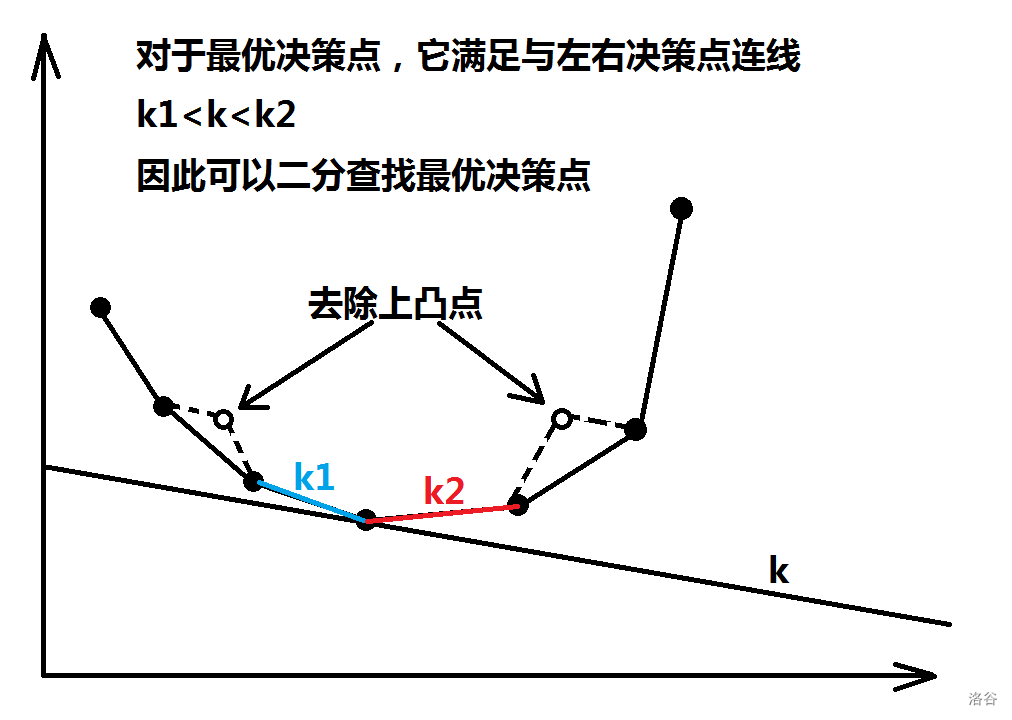
在此，此篇题解就告一段落了，献上代码：

#include <cstdio>
#include <iostream>
typedef long long ll;
const int N = 3e5 + 5 ;
int l = 1 , r = 0 ;
ll sc[N], st[N], f[N], n, s, q[N];
ll Y(int p) {return f[p];}
ll X(int p) {return sc[p];}
ll K(int p) {return s + st[p];}
int Search(int L, int R, long long S) {
	int M = 0 , Res = r ;
	while(L <= R) {
		M = ( L + R ) >> 1; 
		if(Y(q[M + 1]) - Y(q[M]) > S * (X(q[M + 1]) - X(q[M]))) // 由所得性质二分
			R = M - 1, Res = M;
		else L = M + 1; // 二分+-1防止死循环
	}
	return q[Res];
} // 二分查找决策点
int main() {
	scanf("%lld %lld", &n, &s);
	for(int i = 1; i <= n; ++i) {
		scanf("%lld %lld", st + i, sc + i);
		st[i] += st[i - 1];
		sc[i] += sc[i - 1];
	} // 前缀和
	q[++ r] = 0 ;// 0 为第一个决策点
	for(int i = 1; i <= n; ++i) {
		int p = Search(l, r, K(i));
		f[i] = f[p] + s * (sc[n] - sc[p]) + st[i] * (sc[i] - sc[p]); // 按照dp方程式更新答案
		while(l < r && (Y(q[r]) - Y(q[r - 1])) * (X(i) - X(q[r])) 
			>= (Y(i) - Y(q[r])) * (X(q[r]) - X(q[r - 1]))) -- r; // 除去上凸点 ， 这里把算斜率的除法转换为乘法以防误差
		q[++ r] = i; // 入队列
	}
	printf("%lld\n", f[n]); // 完美输出
	return 0; // 好习惯
}

updated on 12-15：毒瘤码风修复，最初方程得出过程已添加