1 条题解
-
0
自动搬运
来自洛谷,原作者为

Stephen_Curry
**搬运于
2025-08-24 22:14:20,当前版本为作者最后更新于2020-03-16 20:44:50,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
2-SAT 模板题
请在完成以下题目后再完成本题。
2-SAT 问题概述
有一个包含 个布尔变量的序列 ,给出一些限制关系要求序列 满足,如 $x_i\And x_j=0,\ x_i\operatorname{or}x_j\operatorname{or}x_k=1$ 等,以此来确定序列 ,这便是 SAT 问题。
若每种限制关系中最多只对 个元素进行限制,则称为 k-SAT 问题。2-SAT 问题就是 时的 SAT 问题。
2-SAT 问题实现
既然有模板题,那这里讲的就尽量简略一点。
结合本题,因为有两个条件,故而我们要一个一个地满足。
每个党派都在委员会中恰有 个代表。
显然这个是很容易满足的,只需跑 Tarjan 求出强连通分量并缩点后若 人同在一个强连通分量中就直接输出
NIE即可。
如果 个代表彼此厌恶,则他们不能都属于委员会。
这也就是 2-SAT 问题较为重要的地方——建边。
举个栗子。
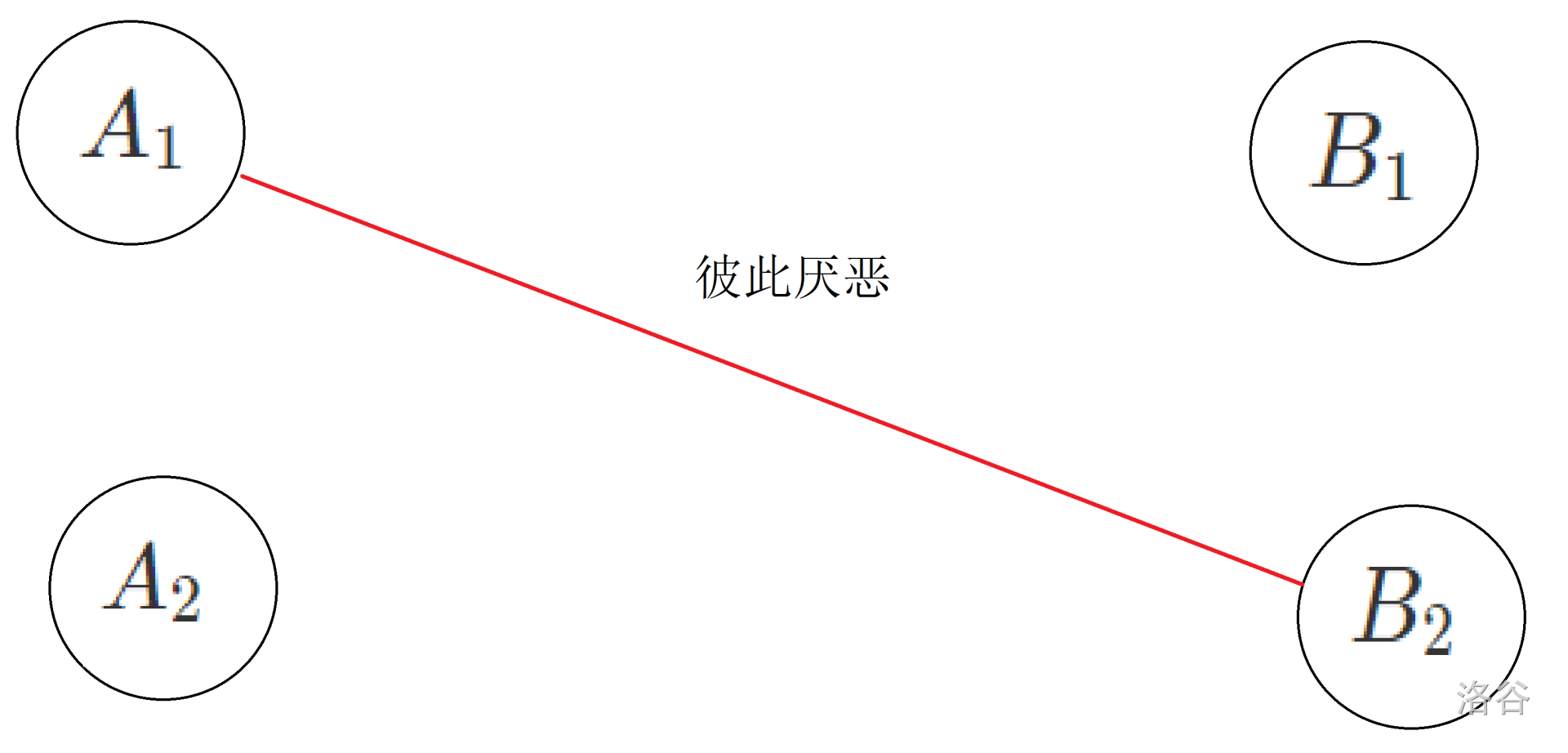
如图,设 与 是任意两个委员会,而 与 彼此厌恶,从而 与 无法连边,于是 只能与 连边, 只能与 连边,从而形成了下图。
$$\tiny\color{#e8e8e8}{\texttt{ps:原图过大洛谷图床上传失败,故而降低了像素,请见谅}} $$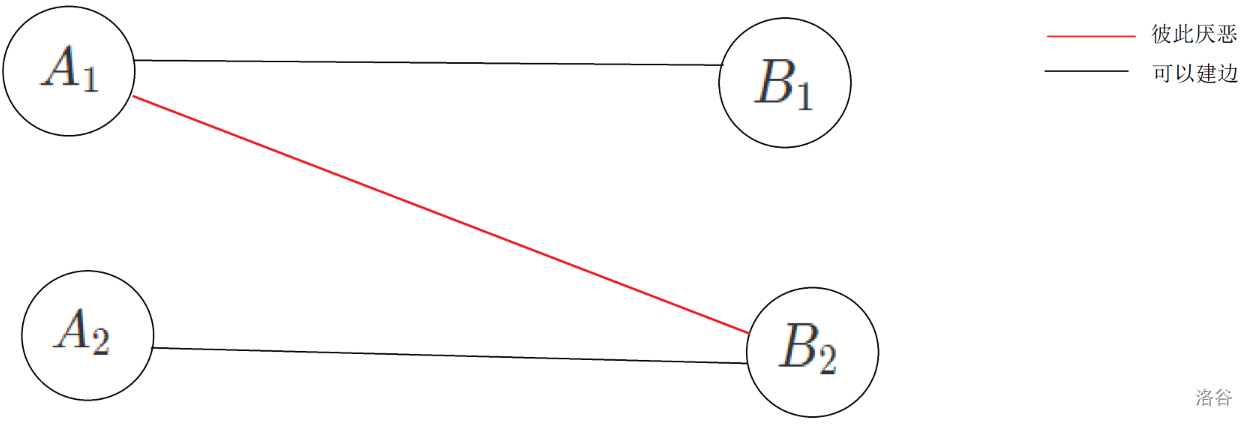
可见,由于有第一个条件的约束,只要将彼此厌恶的双方与对方的搭档连边即可。
附代码片段:
Tarjan 部分:
const int maxm = 50050; const int maxn = 50050; //在空间允许的情况下尽量开大些 struct edge { int u, v, next; } e[maxm]; int p[maxn], eid; void insert(int u, int v) { eid++; e[eid].u = u; e[eid].v = v; e[eid].next = p[u]; p[u] = eid; } //链式前向星 int n, m; int low[maxn], dfn[maxn], times; stack<int> s; bool in[maxn]; int sccno[maxn], scc_cnt; void dfs(int u) { //Tarjan 模板 dfn[u] = low[u] = ++times; s.push(u); in[u] = 1; for (int i = p[u]; i; i = e[i].next) { int v = e[i].v; if (dfn[v] == 0) { dfs(v); low[u] = min(low[u], low[v]); } else if (in[v] == true) low[u] = min(low[u], dfn[v]); } if (low[u] == dfn[u]) { ++scc_cnt; while (true) { int x = s.top(); s.pop(); sccno[x] = scc_cnt; in[x] = 0; if (x == u) break; } } }建边部分:
int fr(int x) { return ((x % 2) ? x + 1 : x - 1); } //-------------------------手动分割线------------------------- while (m--) { int a, b; scanf("%d%d", &a, &b); insert(a, fr(b)); insert(b, fr(a)); }输出部分:
n *= 2; //每个党派有两个代表,所以要乘 2 for (int i = 1; i <= n; ++i) if (i % 2 == 1 and sccno[i] == sccno[i + 1]) //两个代表在同一个强连通分量中,输出 NIE。 return !printf("NIE\n"); for (int i = 1; i <= n; ++i) if (sccno[i] < sccno[fr(i)]) cout << i << "\n";
注意事项
主要是这个菜鸡总是犯低级错误,所以提醒一下。
建双向边数组要开到两倍!建双向边数组要开到两倍!!建双向边数组要开到两倍!!!
这个菜鸡数组没开二倍,结果 #8 #9 #13 #14 死活过不去……
教训啊啊啊(不过数组没开2倍不是 RE 而是 TLE 很奇怪呢……(貌似跑偏了))
- 1
信息
- ID
- 4794
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
