自动搬运

查看原文

来自洛谷，原作者为

	Richard_H 法 小 师

搬运于2025-08-24 22:14:14，当前版本为作者最后更新于2023-11-11 00:13:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

第一问

对于第一问，我们可以打表找规律。我们先用状压枚举长度为 $N$ 的单词，然后用 KMP 判断他是否存在公共前后缀。当然，这个规律事实上不是我看出来的，而是 这位大佬 一眼瞄出来的。打表代码还算好写，在这里就不放了（绝对不是因为不小心已经删掉了），我们令长度为 $i$ 的无界单词的数量为 $p_i$ 的话就有这样的规律。

$$p_i = \begin{cases} p_{i - 1} * 2 & i 为奇数 \\ p_{i - 1} * 2 - p_{\frac i2} & i 为偶数 \end{cases} $$

于是我们可以先预处理出来 $1 \sim 64$ 所有的答案，然后每次询问的第一行直接输出即可。

---

第二问

第二问稍有复杂，需要仔细分析。

首先，要知道一点，如果一个字符串有一个长度超过该字符串长度一半的公共前后缀，则一定存在一个更短的公共前后缀，详见下图。

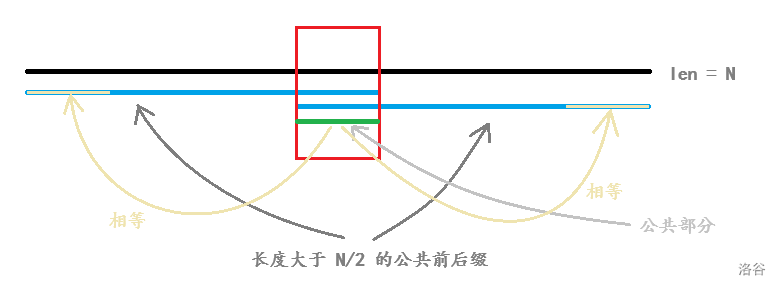
如图中的米黄色部分就是新的公共前后缀。

由此可知，对于每一个不满足要求的字符串，都有一个唯一确定的最短公共前后缀。

再看题目要求，他要问第 $k$ 小的，那么我们结合 Trie 树的思想，从高往低确定每一位是什么。在计算第 $i$ 位时，我们肯定是已经确定了前 $i-1$ 位的，并且知道我们要的答案字符串在确定前 $i - 1$ 位后的排名 $k$，所以我们可以先假设第 $i$ 位是 a，然后算出这种情况下的无界单词的数量 $o$（变量名稍稍有点奇怪），如果 $k$ 在 $o$ 内，那么第 $i$ 位就确定是 a，否则就确定为 b，并更新排名 k -= o，表示该位填 a 一定比填 b 的字典序小。

那么怎么计算在确定了前 $i$ 位后有多少种无界单词呢？这个需要用到容斥原理。用 $f_j$ 表示当前情况下长度为 $j$ 的字符串中有多少个无界单词。如果 $j \leq i$，那么显然可以通过 KMP 算公共前后缀直接得出来。如果 $j > i$ 则需要总方案数减去有公共前后缀的方案数。回想一下上面的结论，如果一个字符串的公共前后缀是最短的，那么他长度一定不超过该字符串长度的一半。而且，如果这个公共前后缀是最短的，那这个公共前后缀自己也一定是无界单词（如果不是的话就取前缀的前缀和后缀的后缀会找到更短的）。所以我们可以枚举该字符串的前缀，来计算需要减掉的方案数。

具体的统计方法就是确定了前后缀的长度和个数后，剩下的位置随便填。计算的时候需要注意有的地方的值已经确定下来了，不能随便填。或者是有的前缀在填成后缀后可能会与已经确定的字符串区间重合，需要特判一下。

具体细节看代码。

---

代码

提交之后直接刷紫，拿下最优解。

#include<iostream>
#include<string.h>
using namespace std;
typedef long long lol;
typedef unsigned long long ull;

const int N = 65;
int T, n, c[N], nxt[N];
ull p[N], k, f[N];

// 更新 i 位置的 nxt[] 数组
void KMP (int &j, int i) 
{
    while (j && c[j + 1] != c[i]) j = nxt[j];
    if (i > 1 && c[j + 1] == c[i]) j ++ ;
}

bool st[N];
ull ahead (int i) 
{
    memset (st, 0, sizeof (st));
    int j = i;
    while (j) 
        st[j] = true, j = nxt[j];
    for (int j (i + 1); j <= (n >> 1); ++ j ) 
    {
        f[j] = 1ull << (j - i);
        for (int t (1); t <= (j >> 1); ++ t ) 
            if (f[t] && (t <= j - i || st[t - j + i]))
                f[j] -= f[t] * (1ll << max (0, j - max (i, t) - t));
    }

    ull ret = 1ull << (n - i);
    for (int j (1); j <= (n >> 1); ++ j ) 
        if (j <= n - i || st[j - n + i]) 
            ret -= f[j] * (1ull << max(0, n - max (i, j) - j));
    return ret;
}

int main () {
    // 预处理第一问答案
    p[0] = 1;
    for (int i = 1; i <= 64; ++ i ) 
        if (i & 1) 
            p[i] = p[i - 1] << 1;
        else 
            p[i] = (p[i - 1] << 1) - p[i >> 1];
    
    scanf ("%d", &T);
    while (T -- ) 
    {
        scanf ("%d%llu", &n, &k);
        printf ("%llu\n", p[n]);

        if (n == 1) 
        {
            putchar (k + 'a' - 1), putchar ('\n');
            continue;
        }

        // 最后一位可以直接通过第一位得到，不用循环到底
        for (int i (1), j (0); i < n; ++ i ) 
        {
            // 假设第 i 的位置上是 a
            c[i] = 0;
            int t = j;
            KMP (j, i), nxt[i] = j, f[i] = !j;
            ull o = ahead (i);
            if (o < k) 
            {
                k -= o;
                // 修改为 b
                c[i] = 1;
                j = t;
                KMP (j, i), f[i] = !j, nxt[i] = j;
            }
        }

        c[n] = !c[1];
        for (int i (1); i <= n; ++ i ) 
            putchar ('a' + c[i]);
        putchar ('\n');
    }
    
    return 0;
}