1 条题解

  • 0
    @ 2025-8-24 22:14:03

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar zhangboju
    屠龙少年终成龙

    搬运于2025-08-24 22:14:03，当前版本为作者最后更新于2020-04-07 22:00:31，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    Update: 感谢 zhangtianhan 指出的错误（将方差与标准差混淆），已纠正。

    LaTeX\LaTeX 有点锅，请在 blog 查看

    题目传送门：Link

    这个题目很重要的条件就是：

    每次切割都只能沿着棋盘格子的边进行。

    关于这个条件的解释，题面中已经写的很清楚了，我就不赘述了。

    考虑使均方差 $\sigma=\sqrt{\dfrac{\sum\limits_{i=1}^{n}(x_i-\bar{x})^2}{n}}$ 最小

    则考虑使方差 $\sigma^2=\dfrac{\sum\limits_{i=1}^{n}(x_i-\bar{x})^2}{n}$ 最小

    分析得到 xˉ=∑i=1nxin\bar{x}=\dfrac{\sum\limits_{i=1}^nx_i}{n} 无论 xix_i 的取值 ，xˉ\bar{x} 恒等于 $\dfrac{\sum\limits_{i=1}^8\sum\limits_{j=1}^8w_{i,j}}{n}$，其中 wi,jw_{i,j} 代表每一个格子上的数。

    所以可以预处理 xˉ\bar{x}。

    此时可以发现将每个 xix_i 分开考虑，使得 (xi−xˉ)2n\dfrac{(x_i-\bar{x})^2}{n} 最小，即考虑使用动态规划。

    由于此题是一个比较明显的区间分割问题，考虑使用区间 DP。

    令 fx1,y1,x2,y2,kf_{x_1,y_1,x_2,y_2,k} 表示将以 (x1,y1)(x_1,y_1) 为左上角，以 (x2,y2)(x_2,y_2) 为右下角的子矩阵划分为 kk 个子矩阵的最小方差 σ2\sigma^2，则最终答案为 f1,1,8,8,n\sqrt{f_{1,1,8,8,n}}。

    此时我们发现要计算子矩阵的和，则考虑二维前缀和。定义 $s_{i,j}=\sum\limits_{q=1}^{i}\sum\limits_{w=1}^{j}w_{q,w}$。

    二位前缀和写法这里不赘述。

    利用 si,js_{i,j}，可 O(1)O(1) 求出子矩阵的和。

    首先定义 ${get}(x_1,y_1,x_2,y_2)=\dfrac{((\sum\limits_{i=x_1}^{x_2}\sum\limits_{j=y_1}^{y_2}w_{i,j})-\bar{x})^2}{n}$

    边界 k=1k=1 时，fx1,y1,x2,y2,1=get(x1,y1,x2,y2)f_{x_1,y_1,x_2,y_2,1}={get}(x_1,y_1,x_2,y_2)。

    在状态转移时，分类讨论水平切还是竖直切，枚举在哪里切，再分类讨论是要哪一块。

    若横向切割：

    1.jpg

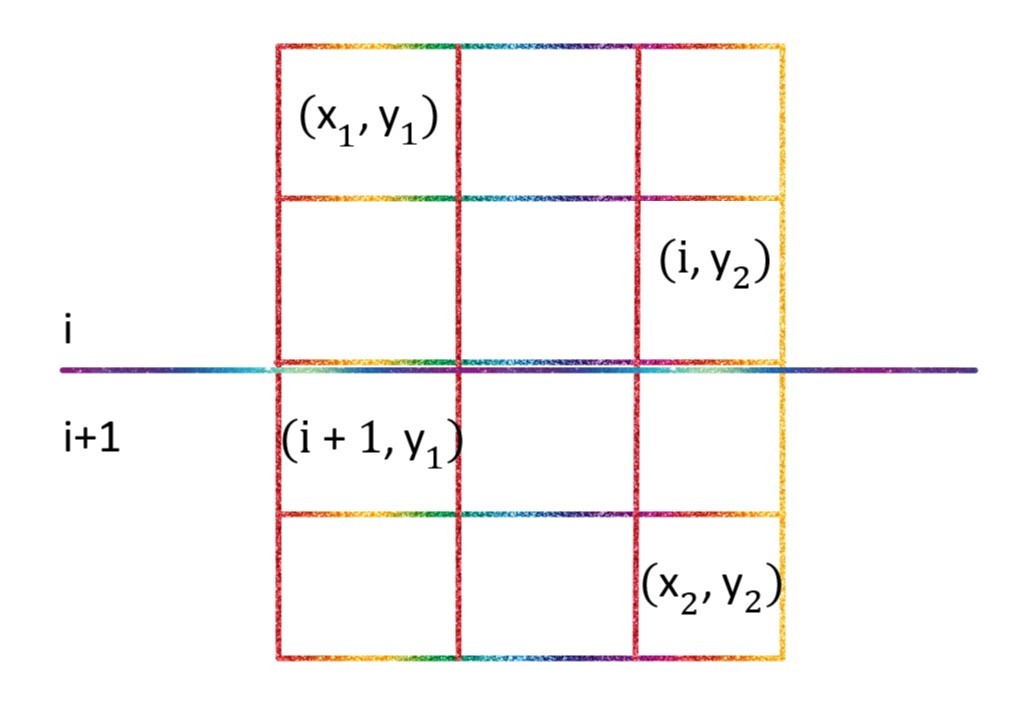
    枚举 i∈[x1,x2)i \in [x_1,x_2) 表示将第 ii 行和第 i+1i+1 行分开，则新的到的两个矩阵左上角和右下角坐标如上图所示。

    若选取上半部分进行再次划分，则 $f_{x_1,y_1,x_2,y_2,k}=f_{x_1,y_1,i,y_2,k-1}+{get}(i+1,y_1,x_2,y_2)$。

    若选取下半部分进行再次划分，则 $f_{x_1,y_1,x_2,y_2,k}=f_{i+1,y_1,x_2,y_2,k-1}+{get}(x_1,y_1,i,y_2)$。

    若纵向切割：

    2.jpg

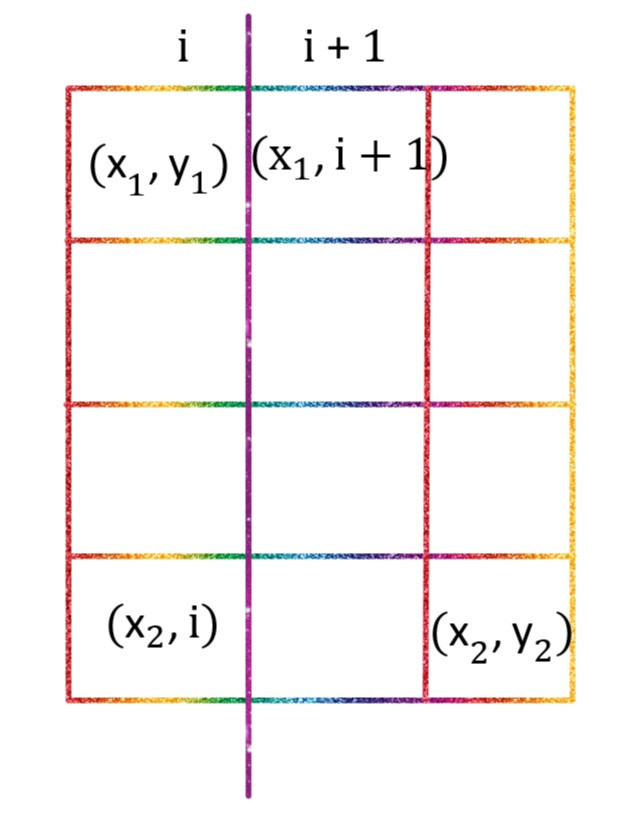
    枚举 i∈[y1,y2)i \in [y_1,y_2) 表示将第 ii 列和第 i+1i+1 列分开，则新的到的两个矩阵左上角和右下角坐标如上图所示。

    若选取上半部分进行再次划分，则 $f_{x_1,y_1,x_2,y_2,k}=f_{x_1,y_1,x_2,i,k-1}+{get}(x_1,i+1,x_2,y_2)$。

    若选取下半部分进行再次划分，则 $f_{x_1,y_1,x_2,y_2,k}=f_{x_1,i+1,x_2,y_2,k-1}+{get}(x_1,y_1,x_2,i)$。

    令 fx1,y1,i,y2,k−1+get(i+1,y1,x2,y2)f_{x_1,y_1,i,y_2,k-1}+{get}(i+1,y_1,x_2,y_2) 为 (1)(1)；

    fi+1,y1,x2,y2,k−1+get(x1,y1,i,y2)f_{i+1,y_1,x_2,y_2,k-1}+{get}(x_1,y_1,i,y_2) 为 (2)(2)；

    fx1,y1,x2,i,k−1+get(x1,i+1,x2,y2)f_{x_1,y_1,x_2,i,k-1}+{get}(x_1,i+1,x_2,y_2) 为 (3)(3)；

    fx1,i+1,x2,y2,k−1+get(x1,y1,x2,i)f_{x_1,i+1,x_2,y_2,k-1}+{get}(x_1,y_1,x_2,i) 为 (4)(4)。

    则可得出状态转移方程：

    $$f_{x_1,y_1,x_2,y_2,k}=\min(\min\limits_{x_1\leq i<x_2}((1),(2))\ \ ,\min\limits_{y_1\leq i< y_2}((3),(4))) $$

    总时间复杂度 O(85n)O(8^5n)。

    由于循环太多，采用记忆化搜索写。

    代码中 X 即为 xˉ\bar{x}。

    注意 X 计算时别忘了强制转换 s 数组的类型。

    #include<bits/stdc++.h>
using namespace std;
double f[9][9][9][9][15];
int s[9][9];
double X;
int n;
double get(int x_1,int y_1,int x_2,int y_2)
{
    double sum=s[x_2][y_2]-s[x_2][y_1-1]-s[x_1-1][y_2]+s[x_1-1][y_1-1]-X;
    return sum*sum/n;
}
double dp(int x_1,int y_1,int x_2,int y_2,int k)
{
    if(f[x_1][y_1][x_2][y_2][k]>=0) return f[x_1][y_1][x_2][y_2][k];
    if(k==1) return f[x_1][y_1][x_2][y_2][k]=get(x_1,y_1,x_2,y_2);
    f[x_1][y_1][x_2][y_2][k]=1e9;
    for(int i=x_1;i<x_2;i++)
    {
        f[x_1][y_1][x_2][y_2][k]=min(f[x_1][y_1][x_2][y_2][k],dp(x_1,y_1,i,y_2,k-1)+get(i+1,y_1,x_2,y_2));
        f[x_1][y_1][x_2][y_2][k]=min(f[x_1][y_1][x_2][y_2][k],dp(i+1,y_1,x_2,y_2,k-1)+get(x_1,y_1,i,y_2));
    }
    for(int i=y_1;i<y_2;i++)
    {
        f[x_1][y_1][x_2][y_2][k]=min(f[x_1][y_1][x_2][y_2][k],dp(x_1,y_1,x_2,i,k-1)+get(x_1,i+1,x_2,y_2));
        f[x_1][y_1][x_2][y_2][k]=min(f[x_1][y_1][x_2][y_2][k],dp(x_1,i+1,x_2,y_2,k-1)+get(x_1,y_1,x_2,i));
    }
    return f[x_1][y_1][x_2][y_2][k];
}
int main()
{
    cin>>n;
    for(int i=1;i<=8;i++)
    {
        for(int j=1;j<=8;j++)
        {
            scanf("%lf",&s[i][j]);
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }
    memset(f,-1,sizeof f);
    X=(double)s[8][8]/n;
    printf("%.3lf\n",sqrt(dp(1,1,8,8,n)));
}

    这个 memset 是一个很玄学的东西，害的我调了半天。

    于是我还是写了一份循环的：

    #include<bits/stdc++.h>
using namespace std;
#define x1 x_1
#define x2 x_2
#define y1 y_1
#define y2 y_2
double f[9][9][9][9][15];
int s[9][9];
double X;
int n;
inline double get(int x1,int y1,int x2,int y2)
{
    double sum=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]-X;
    return sum*sum/n;
}
int main()
{
    cin>>n;
    for(int i=1;i<=8;i++)
    {
        for(int j=1;j<=8;j++)
        {
            cin>>s[i][j];
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }
    X=(double)s[8][8]/n;
    for(int k=1;k<=n;k++)
    {
        for(int x1=1;x1<=8;x1++)
        {
            for(int y1=1;y1<=8;y1++)
            {
                for(int x2=1;x2<=8;x2++)
                {
                    for(int y2=1;y2<=8;y2++)
                    {
                        f[x1][y1][x2][y2][k]=1e9;
                        if(k==1)
                        {
                            f[x1][y1][x2][y2][k]=get(x1,y1,x2,y2);
                            continue;
                        }
                        for(int i=x1;i<x2;i++)
                        {
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][y1][i][y2][k-1]+get(i+1,y1,x2,y2));
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[i+1][y1][x2][y2][k-1]+get(x1,y1,i,y2));
                        }
                        for(int i=y1;i<y2;i++)
                        {
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][y1][x2][i][k-1]+get(x1,i+1,x2,y2));
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][i+1][x2][y2][k-1]+get(x1,y1,x2,i));
                        }
                    }
                }
            }
        }
    }
    printf("%.3lf\n",sqrt(f[1][1][8][8][n]));
}

    再次强调 fx1,y1,x2,y2,kf_{x_1,y_1,x_2,y_2,k} 是存储的将子矩阵 (x1,y1)(x2,y2)(x_1,y_1)(x_2,y_2) 划分为 kk 个子矩阵的最小方差 σ2\sigma^2，所以最后还要开根号！

    当然，这个题还可以采用其他方法。

    同样考虑使方差 $\sigma^2=\dfrac{\sum\limits_{i=1}^{n}(x_i-\bar{x})^2}{n}$ 最小。

    拆开平方：$\sigma^2=\dfrac{1}{n}[\sum\limits_{i=1}^n(x_i^2-2x_i\bar{x}+\bar{x}^2)]$。

    拆开括号：$\sigma^2=\dfrac{1}{n}(\sum\limits_{i=1}^nx_i^2-2\bar{x}\sum\limits_{i=1}^nx_i+n\bar{x}^2)=\dfrac{\sum\limits_{i=1}^nx_i^2}{n}-2\bar{x}\dfrac{\sum\limits_{i=1}^nx_i}{n}+\bar{x}^2$。

    而我们知道：xˉ=∑i=1nxin\bar{x}=\dfrac{\sum\limits_{i=1}^nx_i}{n}。

    所以：$\sigma^2=\dfrac{\sum\limits_{i=1}^nx_i^2}{n}-\bar{x}^2$。

    要使 σ2\sigma^2 最小，由于 xˉ2\bar{x}^2 为定值，则使 ∑i=1nxi2n\dfrac{\sum\limits_{i=1}^nx_i^2}{n} 最小。

    此时改变 fx1,y1,x2,y2,kf_{x_1,y_1,x_2,y_2,k} 的意义，表示将以 (x1,y1)(x_1,y_1) 为左上角，以 (x2,y2)(x_2,y_2) 为右下角的子矩阵划分为 kk 个子矩阵的最小的 ∑i=1kxi2n\dfrac{\sum\limits_{i=1}^kx_i^2}{n}。

    改变 ${get}(x_1,y_1,x_2,y_2)=\dfrac{(\sum\limits_{i=x_1}^{x_2}\sum\limits_{j=y_1}^{y_2}w_{i,j})^2}{n}$。

    则最后答案为 f1,1,8,8,n−xˉ2\sqrt{f_{1,1,8,8,n}-\bar{x}^2}。

    状态转移方程不变。

    代码：

    #include<bits/stdc++.h>
using namespace std;
#define x1 x_1
#define x2 x_2
#define y1 y_1
#define y2 y_2
double f[9][9][9][9][15];
int s[9][9];
double X;
int n;
inline double get(int x1,int y1,int x2,int y2)
{
    double sum=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
    return sum*sum/n;
}
int main()
{
    cin>>n;
    for(int i=1;i<=8;i++)
    {
        for(int j=1;j<=8;j++)
        {
            cin>>s[i][j];
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }
    X=(double)s[8][8]/n;
    for(int k=1;k<=n;k++)
    {
        for(int x1=1;x1<=8;x1++)
        {
            for(int y1=1;y1<=8;y1++)
            {
                for(int x2=1;x2<=8;x2++)
                {
                    for(int y2=1;y2<=8;y2++)
                    {
                        f[x1][y1][x2][y2][k]=1e9;
                        if(k==1)
                        {
                            f[x1][y1][x2][y2][k]=get(x1,y1,x2,y2);
                            continue;
                        }
                        for(int i=x1;i<x2;i++)
                        {
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][y1][i][y2][k-1]+get(i+1,y1,x2,y2));
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[i+1][y1][x2][y2][k-1]+get(x1,y1,i,y2));
                        }
                        for(int i=y1;i<y2;i++)
                        {
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][y1][x2][i][k-1]+get(x1,i+1,x2,y2));
                            f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][y2][k],f[x1][i+1][x2][y2][k-1]+get(x1,y1,x2,i));
                        }
                    }
                }
            }
        }
    }
    printf("%.3lf\n",sqrt(f[1][1][8][8][n]-X*X));
}
    • 1

    [NOI1999] 棋盘分割

    信息

    ID
    4763
    时间
    1000ms
    内存
    125MiB
    难度
    4
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 39ms