1 条题解
-
0
自动搬运
来自洛谷,原作者为

fzwfzwfzw
Haven't AFO yet.搬运于
2025-08-24 22:14:02,当前版本为作者最后更新于2020-06-08 20:59:08,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
我们来看一下这道题:
如果所有钉子都还在,那么
小球落在第 个格子中的概率为
= =
其实这道题是一个dp,我们发现 ()所以,我们可以n方暴力做

我们设一个个的小格子中的概率为
因为我们要求的为一个最简分数,所以
表示分子,表示分子,这是个既约分数
我们可以发现

落在这个位置的小球概率为1,所以
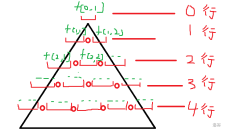
我们通过观察法可以得到,如果在的正下方
有
钉子,那么
有 的概率落在 上,
有 的概率落在 上
但是如果我们拔掉一个钉子
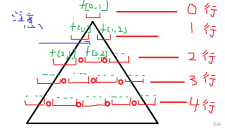
就只有可能落在上面,所以我们得到
如果在的正下方
没有
钉子,那么
落在 上
所以dp方程就出来了,初始值为
表示是否有钉子
若则$f[i][j]+=\frac{f[i-1][j]}{2},f[i][j+1]+=\frac{f[i-1][j]}{2}$
若则
如果有不理解的地方可以私信我!
下面是代码时间!!!
注意,要写一个分数类出来(就是重载一下运算符代码里面有解释)!
#include<bits/stdc++.h> using namespace std; int read() { char c; int w=1; while((c=getchar())>'9'||c<'0')if(c=='-')w=-1; int ans=c-'0'; while((c=getchar())>='0'&&c<='9')ans=(ans<<1)+(ans<<3)+c-'0'; return ans*w; } long long gcd(long long a,long long b)//欧几里得算法 { return b==0?a:gcd(b,a%b); } struct node { long long a,b; void huajian()//让该分数成为既约分数 { long long w=gcd(a,b); a=a/w; b/=w; } node operator /(const long long y)const//一个分数除以一个整数 { node t = *this; t.b *= y,t.huajian(); return t; } node operator +(node y)const//一个分数加上另外一个分数 { if(a==0) { y.huajian(); return y; } node o=*this; if(y.a==0) { o.huajian(); return o; } long long p=gcd(o.b,y.b); o.a*=(y.b/p);o.a+=y.a*(o.b/p);o.b*=(y.b/p); o.huajian(); return o; } }f[1005][1005];//其实只要开50就够了! int n,m; int c[1005][1005]; int main(){ n=read(); m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=i;j++) { char w; while((w=getchar())!='*'&&w!='.'); if(w=='*')c[i][j]=1; } } f[0][1].a=1;//初始化 f[0][1].b=1; for(int i=1;i<=n+1;i++) { for(int j=1;j<=n+1;j++) { f[i][j].b=1;//注意要吧所有分数初始化一下,不然除以0化简时会RE } } for(int i=1;i<=n;i++) { for(int j=1;j<=i;j++) { if(c[i][j]) { node p=f[i-1][j];//有钉子的时候 p=p/2; f[i][j]=f[i][j]+p; f[i][j+1]=f[i][j+1]+p; } else { f[i+1][j+1]=f[i+1][j+1]+f[i-1][j];//没有钉子的时候 } } } for(int i=1;i<=n;i++) for(int j=1;j<=i+1;j++) { f[i][j].huajian();//记得要化简哟!!! } f[n][m+1].huajian(); cout<<f[n][m+1].a<<"/"<<f[n][m+1].b<<endl;//cout大发好 return 0; }祝大家好运!
- 1
信息
- ID
- 4761
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
