自动搬运

查看原文

来自洛谷，原作者为

	旭日临窗 **

搬运于2025-08-24 22:13:21，当前版本为作者最后更新于2020-10-04 17:10:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路：

正难则反，求最多能拆除多少条道路不是太好求，所以我们可以求出最少用多少条道路能满足题目条件，最后再用$m$减去不就可以了吗，一说到最少留多少条路，考虑最短路。

那我们能直接把$A$到$s1$的最短路和$A$到$s2$的最短路加起来吗？

显然是不可以的，以为拆到最后有两种可能，如图：

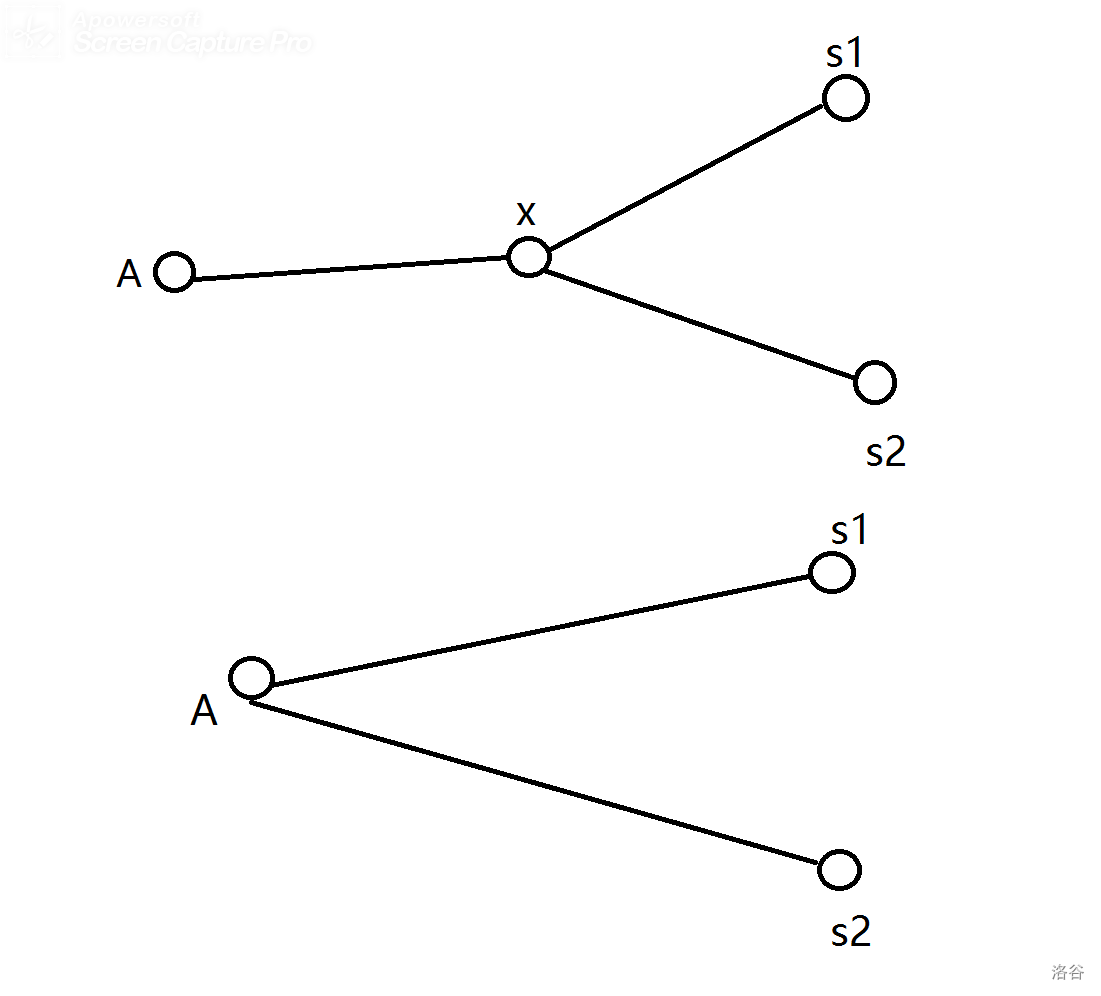
但是我们发现，第二种属于第一种可能，可以看做是$x$点与$A$点重了而已。

所以我们可以遍历所有点$x$，定义$x\to y$表示$x$到$y$的最短路，找出

$\sum\limits_{x=1}^{n}\min(A\to x + x\to s1 + x\to s2)$即可，但这样复杂度就太高了，观察发现$A$，$s1$，$s2$，是不变的，因为是双向边，所以$x\to s1==s1\to x$，$s2$也一样。

$code$：

#include <bits/stdc++.h>
using namespace std; 
const int inf = 0x7f7f7f7f;
int n,m,cnt,s1,t1,s2,t2,ans = inf;
int dis1[3010],dis2[3010],dis3[3010];
vector <int> G[3010];//邻接表存边。 
queue <int> q;
inline int read()//快读。 
{
	cnt = 0;
	char c;
	while((c = getchar()) < '0' || c > '9');
	while(c >= '0' && c <= '9') cnt = cnt * 10 + (c - '0'),c = getchar();
	return cnt;
}
void bfs(int s,int *dis)//最短路模板，不多说了。 
{
	q.push(s);
	dis[s] = 0;
	while(!q.empty())
	{
		int u = q.front();q.pop();
		for(int i = 0;i < G[u].size();i++)
		{
			int v = G[u][i];
			if(dis[u] + 1 < dis[v])
			{
				dis[v] = dis[u] + 1;
				q.push(v);
			}
		}
	}
}
int main()
{
	n = read(),m = read();
	int x,y;
	for(int i = 1;i <= m;i++)
	{
		x = read(),y = read();
		G[x].push_back(y);//注意是双向边。 
		G[y].push_back(x);
	}
	s1 = read(),t1 = read(),s2 = read(),t2 = read();
	memset(dis1,inf,sizeof(dis1));
	memset(dis2,inf,sizeof(dis2));
	memset(dis3,inf,sizeof(dis3));
	bfs(1,dis1);//预处理三次最短路。 
	if(dis1[s1] > t1 || dis1[s2] > t2)//如果不拆路都没法满足条件，那拆路就更没法满足了，直接输出-1。 
	{
		puts("-1");
		return 0;
	}
	bfs(s1,dis2);
	bfs(s2,dis3);
	for(int i = 1;i <= n;i++)//遍历所有点x。 
	if(dis1[i] + dis2[i] <= t1 && dis1[i] + dis3[i] <= t2)//如果满足条件就更新ans。 
	ans = min(ans,dis1[i] + dis2[i] + dis3[i]);
	printf("%d",m - ans);//正难则反，输出总道路数减去最少保留数即可。 
	return 0;
}

/管理员大大求过$thanks$/