自动搬运

查看原文

来自洛谷，原作者为

	syksykCCC 相信并抓住那些源于热爱，忠于自我的每一个可能性

搬运于2025-08-24 22:13:09，当前版本为作者最后更新于2019-12-01 10:09:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

UPD：官方数据出来，原题解无法通过。现在已经常数优化，保险起见，评测请开启 O2。

（一年半后）UPD2：经过一晚上的卡常，手写高精度终于在不开 O2 的情况下稳稳地通过了这题！

既当作是一个赛场自己没做出来的总结，也给那些不愿使用 __int128 的同学们一篇可以参考的题解吧。

首先由 完全平方公式 ，可以得到 $(a + b)^2 \ge a^2 + b^ 2$。

所以，我们要尽可能 多分段。

观察这个图：

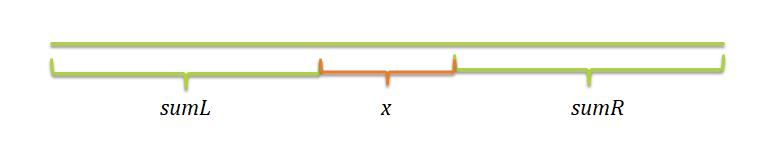
如果此时，$sum_L + x \le sum_R$，那么 $x$ 这个数应该分到那一边呢？

显然，$sum_L \le sum_R$，$x$ 加到 $side$ 那边 将会产生 $2x\cdot sum_{side}$ 的代价。

为了使得总代价最小，我们当然把 $x$ 加到 $sum_L$ 那一边啦！

综上所述，对于某一段，我们贪心的在最靠后的可行位置划分，也就是使得最后一段最小，答案必然最优。

64pts 的做法是贪心的记录这一段的值，枚举 上一段的终点。

大概就是这样：

for(int i = 2; i <= n; ++i)
    for(int j = 1; j < i; ++j)
        if(sum[i] - sum[j] >= last[j] && f[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]) < f[i])
            f[i] = f[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]), last[i] = sum[i] - sum[j];

$last_i$ 表示以 $i$ 结尾的那一段的和，$f_n$ 即为答案。

那 100pts 的做法呢？

用 $g_i$ 表示现在划分段的末尾为 $i$ ，上一段的末尾。

用 $s_i$ 表示 $\sum_{k = 1}^{i} a_k$（前缀和）。

换言之， $g_i = \max pos\ s.t. \ s_i - s_{pos} \ge s_{pos} - s_{g_{pos}}$。

移项得到，$g_i = \max pos\ s.t. \ s_i \ge 2s_{pos} - s_{g_{pos}}$。

令 $val(x) = 2 s_x-s_{g_x}$，则$g_i = \max pos\ s.t. \ s_i \ge val(pos)$，有结论：

如果 $x, y$ 都是当前位置 $i$ 的合法来源，即 $s_i \ge val(x), val(y)$，而且 $x<y$，则 $x$ 必然 无法成为 $g_i$。

由此，当求 $g_i$ 时，先把单调队列中所有队首的过时决策弹出（如果队列中的下一个数的 $val$ 都 $\le s_i$ 的话，这个决策就被弹出）。

$g_i$ 就是 新的队首 ，然后把 $i$ 加入决策时，要把队尾所有 $val \ge val(i)$ 的弹出（因为 $i$ 在它们 后面 ，$val$ 还比它们 小 ，那它们必然 不会成为 任何一个位置的 $g$ 了）。

最后一段的末端点是 $n$，所以让 $p = n$，不断的朝 $g_p$ 追溯，并统计答案。

注意时间优化，空间优化，高精度，时间复杂度 $O(n)$。

前缀和不用平方，不要开 高精度数组 ！

代码如下:

#include <stdio.h>
#include <ctype.h>
#include <memory.h>
#define rg register
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
#define val(x) (s[x] << 1) - s[g[x]]
typedef unsigned long long ULL;
const int MOD = (1 << 30) - 1, N = 4e7 + 3, M = 1e5 + 3, BASE = 1e9;
int g[N], b[N], p[M], q[N];
ULL s[N];
char buf[1 << 21], *p1 = buf, *p2 = buf;
inline int read()
{
    int val = 0; char c = gc();
    while(!isdigit(c)) c = gc();
    while(isdigit(c)) { val = (val << 3) + (val << 1) + (c ^ 48); c = gc(); }
    return val;
}
struct bigint
{
    int len;
    ULL num[4];
    bigint operator + (const bigint &oth)
    {
        bigint res; 
        memset(res.num, 0, sizeof(res.num));
        res.len = len > oth.len ? len : oth.len; rg ULL p = 0;
        for(rg int i = 0; i < res.len; i++) 
        {
            res.num[i] = num[i] + oth.num[i] + p;
            p = res.num[i] / BASE;
            res.num[i] -= BASE * p;
        }
        if(p) res.num[res.len++] = p;
        return res;
    }
} ans;
int main()
{
    int n = read(), type = read();
    if(type)
    {
        ULL x, y; int z, m, l, r;
        x = read(); y = read(); z = read(); b[1] = read(); b[2] = read(); m = read();
        for(rg int i = 3; i <= n; i++) b[i] = (x * b[i - 1] & MOD) + (y * b[i - 2] & MOD) + z & MOD;
        for(rg int j = 1; j <= m; j++)
        {
        	p[j] = read(); l = read(); r = read();
        	for(rg int i = p[j - 1] + 1, a; i <= p[j]; s[i] = s[i - 1] + a, i++)
                a = b[i] % (r - l + 1) + l;
		}
    }
    else for(rg int i = 1, a; i <= n; s[i] = s[i - 1] + a, i++) a = read();
   	rg int head = 1, tail = 1;
    for(rg int i = 1; i <= n; i++)
    {
        while(head < tail && val(q[head + 1]) <= s[i]) head++;
        g[i] = q[head];
        while(head <= tail && val(q[tail]) >= val(i)) tail--;
        q[++tail] = i;
    }
    ans.len = 0;
    for(rg int pos = n; pos; pos = g[pos])
    {
        bigint tmp, res; ULL val = s[pos] - s[g[pos]];
        tmp.len = 0;
        while(val) { tmp.num[tmp.len++] = val % BASE; val /= BASE; }
	    memset(res.num, 0, sizeof(res.num));
	    res.len = (tmp.len << 1) - 1; ULL p = 0;
	    for(rg int i = 0; i < tmp.len; i++) for(rg int j = 0; j < tmp.len; j++)
	        res.num[i + j] += tmp.num[i] * tmp.num[j];
	    for(rg int i = 0; i < res.len; i++)
	    {
	        res.num[i] += p;
	        p = res.num[i] / BASE;
	        res.num[i] -= BASE * p;
	    }
	    while(p) { res.num[res.len++] = p % BASE; p /= BASE; }
        ans = ans + res;
    }
    printf("%llu", ans.num[ans.len - 1]); for(rg int i = ans.len - 2; ~i; i--) printf("%09llu", ans.num[i]);
    return 0;
}