自动搬运

查看原文

来自洛谷，原作者为

	小粉兔 Always continue; Never break;

搬运于2025-08-24 22:13:00，当前版本为作者最后更新于2019-11-14 11:22:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意简述：

题目说得很清楚了。

题解：

观察这个函数，$\displaystyle F(l, r) = \max(F(l, m-1), F(m+1, r)) + w_m$。

很显然，当询问 $F(1, n)$ 时，转移就是一个笛卡尔树的结构。笛卡尔树的构建可以使用单调栈。

考虑询问 $l, r$ 时，区间 $[l, r]$ 形成的笛卡尔树：

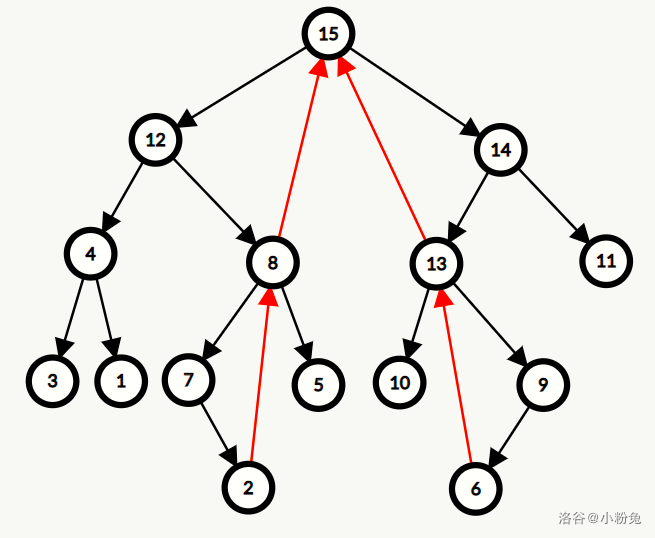
上图为序列 $p = \{3, 4, 1, 12, 7, 2, 8, 5, 15, 10, 13, 6, 9, 14, 11\}$ 的笛卡尔树。

当询问 $\left< l, r \right> = \left< 6, 12 \right>$ 时，即有 $p_6 = 2$，$p_{12} = 6$，两条红色链两侧的点和边全部删除，并添加红色边，得到的即是这个区间中的笛卡尔树。

首先有区间的笛卡尔树的根节点应该是这两个点在原笛卡尔树上的 LCA，只不过在这个例子中恰好是根。

可以发现点 $8$ 即是点 $2$ 祖先中第一个往“右”走的点，而点 $15$ 也是点 $8$ 的祖先中第一个往“右”走的点。右边的 $6 \to 13 \to 15$ 同理，只不过左右交换了。

也就是说，区间 $[l, r]$ 的笛卡尔树的“左链”和“右链”由这种方式确定，而中间的子树没有改动。

令 $z = \mathrm{lca}(l, r)$，则答案为 $\max(F(l, z-1), F(z+1, r)) + w_z$。也就是将式子展开一层，左右两边分开考虑，最后再合起来。

以左侧的 $F(l, z-1)$ 为例，它也就是 $z$ 的左子树（但是其“左链”由 $l$ 用刚刚的方式确定）。

考虑使用倍增，从 $l$ 通过红色边不断尝试向上跳 $2^j$ 步到达 $z$，并统计这之间产生的贡献。

注意：这里说的祖先都是不断通过红色边上升到达的点，而不是原笛卡尔树的祖先。
红色边：$\boldsymbol u$ 通过红色边的父亲即是 $\boldsymbol u$ 在原笛卡尔树的祖先链中，最深的往“右”走（即上一个点是它的左孩子）的点，如果不存在这样的点则没有通过红色边的父亲（在原笛卡尔树的“右链”上才可能没有父亲）。

首先预处理 $f(u, j)$ 表示 $u$ 的最近 $2^j$ 个祖先（包含 $u$）的 $w$ 之和，以及 $g(u, j)$ 表示 $u$ 的 $2^j - 1$ 次祖先的子树（删去 $\boldsymbol u$ 之前的点）内的答案（但强制不能往 $u$ 的左子树走，即使 $u$ 的左子树确实是空的，这是因为合并答案时需要接在上面，而答案有可能是负的，会影响计算）。

上述预处理不难合并，具体可以看代码。

查询的时候也是同理，从 $l$ 往上，令 $j$ 从大到小不断尝试能否跳到 $z$ 或比 $z$ 深的节点，能跳就跳并更新答案。

对 $F(z+1, r)$，即 $z$ 的右子树也是同理，只不过要把方向反一下，这里不再赘述。

总结：不需要用到任何数据结构，仅需掌握笛卡尔树和倍增的知识点，实乃小清新树上问题（大雾）

总结：注意卡空间，因为倍增的空间消耗很大，而且很多数组要开 long long 类型，不得不合并一些预处理数组，而且还需左右两边分开处理，不占用重复空间才卡过去。

#include <cstdio>
#include <cstring>
#include <algorithm>

#define _L_ 0
#define _R_ 1
int lr;

typedef long long LL;
const int MN = 500005, MQ = 500005;

int N, Q, root, A[MN], V[MN];

int dep[MN], lc[MN], rc[MN], faz[MN][19];
LL S[MN], _chain[MN][19], _subt[MN][19];
void DFS0(int u) {
	for (int j = 0; j < 18 && faz[u][j]; ++j) faz[u][j + 1] = faz[faz[u][j]][j];
	if (lc[u]) dep[lc[u]] = dep[u] + 1, DFS0(lc[u]);
	if (rc[u]) dep[rc[u]] = dep[u] + 1, DFS0(rc[u]);
	S[u] = std::max(S[lc[u]], S[rc[u]]) + V[u];
}
void Init() {
	static int stk[MN]; int tp = 0, x;
	for (int i = 1; i <= N; ++i) {
		x = 0;
		while (tp && A[stk[tp]] < A[i]) {
			if (x) rc[stk[tp]] = x, faz[x][0] = stk[tp];
			x = stk[tp], --tp;
		}
		if (x) lc[i] = x, faz[x][0] = i;
		stk[++tp] = i;
	}
	x = 0;
	while (tp) {
		if (x) rc[stk[tp]] = x, faz[x][0] = stk[tp];
		x = stk[tp], --tp;
	}
	dep[x] = 1, DFS0(x);
	root = x;
}

inline int lca(int u, int v) {
	if (dep[u] < dep[v]) std::swap(u, v);
	for (int d = dep[u] - dep[v], j = 0; d; d >>= 1, ++j)
		if (d & 1) u = faz[u][j];
	if (u == v) return u;
	for (int j = 18; j >= 0; --j)
		if (faz[u][j] != faz[v][j])
			u = faz[u][j],
			v = faz[v][j];
	return faz[u][0];
}

void DFS1(int u) {
	_chain[u][0] = V[u];
	if (lr == _L_) _subt[u][0] = S[lc[u]] + V[u];
	if (lr == _R_) _subt[u][0] = S[rc[u]] + V[u];
	for (int j = 0; j < 18; ++j) {
		faz[u][j + 1] = faz[faz[u][j]][j];
		if (!faz[u][j + 1]) break;
		_chain[u][j + 1] = _chain[u][j] + _chain[faz[u][j]][j];
		_subt[u][j + 1] = std::max(_chain[faz[u][j]][j] + _subt[u][j], _subt[faz[u][j]][j]);
	}
	if (lc[u]) {
		if (lr == _L_) faz[lc[u]][0] = faz[u][0];
		if (lr == _R_) faz[lc[u]][0] = u;
		DFS1(lc[u]);
	}
	if (rc[u]) {
		if (lr == _L_) faz[rc[u]][0] = u;
		if (lr == _R_) faz[rc[u]][0] = faz[u][0];
		DFS1(rc[u]);
	}
}

inline LL calc(int u, int z) {
	LL val = 0;
	for (int j = 18; j >= 0; --j)
		if (dep[faz[u][j]] >= dep[z]) {
			val = std::max(val + _chain[u][j], _subt[u][j]);
			u = faz[u][j];
		}
	return val;
}

int ql[MQ], qr[MQ], qz[MQ];
LL Ans[MQ];

int main() {
	scanf("%d%d", &N, &Q);
	for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
	for (int i = 1; i <= N; ++i) scanf("%d", &V[i]);
	Init();
	for (int i = 1; i <= Q; ++i) {
		scanf("%d%d", &ql[i], &qr[i]), qz[i] = lca(ql[i], qr[i]);
		Ans[i] = -0x3f3f3f3f3f3f3f3f;
	}
	memset(faz, 0, sizeof faz), lr = _R_, DFS1(root);
	for (int i = 1; i <= Q; ++i) Ans[i] = std::max(Ans[i], calc(ql[i], qz[i]) + V[qz[i]]);
	memset(faz, 0, sizeof faz), lr = _L_, DFS1(root);
	for (int i = 1; i <= Q; ++i) Ans[i] = std::max(Ans[i], calc(qr[i], qz[i]) + V[qz[i]]);
	for (int i = 1; i <= Q; ++i) printf("%lld\n", ql[i] <= qr[i] ? Ans[i] : 0ll);
	return 0;
}