自动搬运

查看原文

来自洛谷，原作者为

	无意识躺枪人 是OwenOwl的小迷妹 | cdqz最菜OIer

搬运于2025-08-24 22:12:59，当前版本为作者最后更新于2019-11-13 18:54:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

吹爆这道题！

真的超级爱这题啊！

可以给这篇题解点下赞吗qwq

在这里把考场上的思路完整的说一下

首先考虑倒推，如果最后一格的数是奇数，会怎么样？

以样例为例

显然，如果我们走到了最后一格，就只能在上面反复横跳，直到这一列的格子完全消失

很容易发现，这样的情况，最后一列就是一个必胜点（这里必胜点定义为先走到这里一定获胜）

那么，在这一列前面m-1列之内，所有列都是必败点（因为如果走到这里，下一步对手一定可以走到必胜点）

用红色表示必胜点，蓝色表示必败点

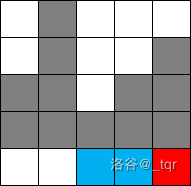
接着继续考虑，如果要尽量避免走到蓝色的列（必败点），最后两人一定会在第二列上反复横跳，直到这一列消失

是不是很熟悉？对！这是和最开始情况一样的！

但这里，最后一格是偶数，显然它是必败点（先手过去一定会输）

那它前面那一列是什么点呢？因为是偶数，所以继承了前面的情况，也是必败点

到这里，我们已经可以得出一个结论了：

倒推，如果最后一列是奇数，那么这一列是必胜点，它前面的m-1列都必败
如果最后一列是偶数，那么这一列是必败点，所有玩家都会尽量避免走到这一列来

所以我们可以考虑连边！顺序枚举，对于每一列，把它前面的第一个必胜点向他连边，这样的话，连好后的图是一个多叉树形结构！

对于每次的询问l和r，如果l是r的祖先，那么先手必胜，否则后手必胜！

那么现在的问题来了，给出一棵固定形态的树，怎么$\Theta(1)$地判断u是否是v的祖先呢？

dfs序！

在dfs的过程中统计一个点第一次被访问到的时间戳，作为其dfn

如果$dfn[u]\leq dfn[v] \leq dfn[u]+size[u]-1$的话，u就是v的祖先！

那么这题就这样解决啦！

具体的看代码吧

#include<bits/stdc++.h>
#define mod (1LL<<32)
#define ll long long
#define int long long
#define N 20000005
using namespace std;

int n,m,q,type,l[N],r[N];
int L,a[N],fa[N];//fa->这个点前面的第一个必胜转移点 
ll ans=0;

int A,B,C,P;
inline int rnd(){return A=(A*B+C)%P;}

struct Edge
{
	int next,to;
}edge[N];
int cnt=0,head[N];

inline void add_edge(int from,int to)
{
	edge[++cnt].next=head[from];
	edge[cnt].to=to;
	head[from]=cnt;
}

template<class T>inline void read(T &res)
{
	char c;T flag=1;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
	while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}

int siz[N],dfn[N],tms;
void dfs(int u,int fa)
{
//	cout<<"dfs: "<<u<<" "<<fa<<endl;
	siz[u]=1;
	if(!dfn[u]) dfn[u]=++tms;
	for(register int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa) continue;
		dfs(v,u);
		siz[u]+=siz[v];
	}
}

signed main()
{
	read(n);read(m);read(q);read(type);//数的个数，区间长度，询问，是否压缩 
	for(register int i=1;i<=n;++i) read(a[i]);
	if(!type)
	{
		for(register int i=1;i<=q;++i)
			read(l[i]),read(r[i]);
	}
	else
	{
		read(A);read(B);read(C);read(P);
		for(register int i=1;i<=q;++i)
		{
			l[i]=rnd()%n+1;
			r[i]=rnd()%n+1;
			if(l[i]>r[i]) swap(l[i],r[i]);
		}
	}
	
	for(register int i=1;i<=n;++i)
	{
		L=max(0LL,i-m-1);
		if(a[i]&1)//奇数是必胜点
		{
			if(a[L]&1) fa[i]=L,add_edge(L,i);
			else fa[i]=fa[L],add_edge(fa[L],i);
		}
		else//偶数，先手必败 
		{
			if(a[i-1]&1) fa[i]=i-1,add_edge(i-1,i);
			else fa[i]=fa[i-1],add_edge(fa[i-1],i);
		}
	}
	//处理出每个点倒序第一个必胜转移点 

	dfs(0,0);//dfs序 
//	for(register int i=1;i<=n;++i) cout<<siz[i]<<endl;
	for(register int i=1;i<=q;++i)
	{
		int u=l[i],v=r[i];
		if(u==v)
		{
			if(a[u]&1) continue;
			else ans=(ans+i*i)%mod;
			continue;
		}
//		cout<<dfn[u]<<" "<<dfn[v]<<" "<<dfn[u]+siz[u]-1<<endl;
		if(dfn[u]<=dfn[v]&&dfn[v]<=dfn[u]+siz[u]-1) continue;//先手必胜，没有贡献 
		ans=(ans+i*i)%mod;
	}
	printf("%lld\n",ans);
	return 0;
}

/*
4 2 1 0
2 2 0 0
1 4
*/