1 条题解
-
0
自动搬运
来自洛谷,原作者为

EnofTaiPeople
MGXS搬运于
2025-08-24 22:12:56,当前版本为作者最后更新于2022-10-13 20:55:24,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
Part1 前言
P5649 Sone1 是一个神奇的题,用 个字概括:
链加链赋值,最值与求和,子树加赋值,最值与求和,换根换父亲。可以认为是一道解法很多的开放题。
Part2 重工业理论与实现细节
的原理是使用
splay维护实路径,这样可以实现平摊 实现链修改,链查询。为了对虚儿子进行维护,我们应当新开一个
splay维护虚儿子,编号为 。每一个父亲记录其虚儿子
splay的根节点,注意,只有isroot(x), 才有意义。事实上,实路径和虚子树的
splay可以共用,在实路径splay时,需要将原来的根节点从虚子树中删除,再将新的根节点插入,复杂度瓶颈就在此处。这样来说,如果把虚子树根看作中儿子,这就是三度化的 。
但我还是看不懂 ,由于找前驱后继无法平摊,所以时间为 。
用 来维护虚儿子可以做到 的
access。但这样无法共用
splay,码长要翻一倍,这也称为 。重工业还有一个特点,把
tag看作一次函数,将dat打包,省去了addtag和pushdown的分类讨论,进一步减小码量,当然这个也可以单纯地用矩阵乘法来理解。具体实现要记录两个标记,表示链上修改和链外(虚子树)修改,还要记录三个数据,表示链上和,链外(虚子树)和,还有自己的值。
贴上评测链接。
Part3 从 理论到
显然,大多数大佬能看懂论文哥的文章。
但实现部分我是观察 AC 代码才理解的。
如果你只想学一种动态树而不愿意多做研究,那么只需要能理解 理论,那么你也能看懂 的实现过程。
但在读下文前,请先将论文哥的文章先读三遍,可以大致理解一下 理论。
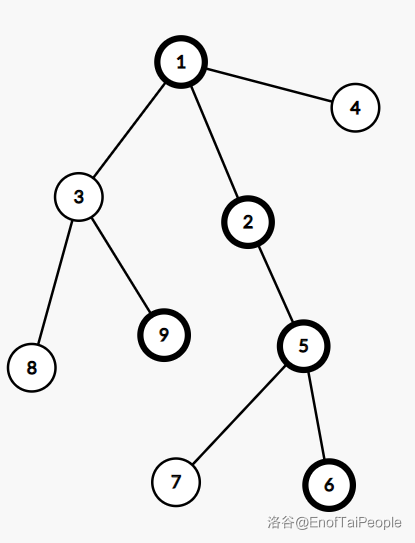
上图是一棵树,加粗的点表示实儿子,这棵树所对应的 如下图:
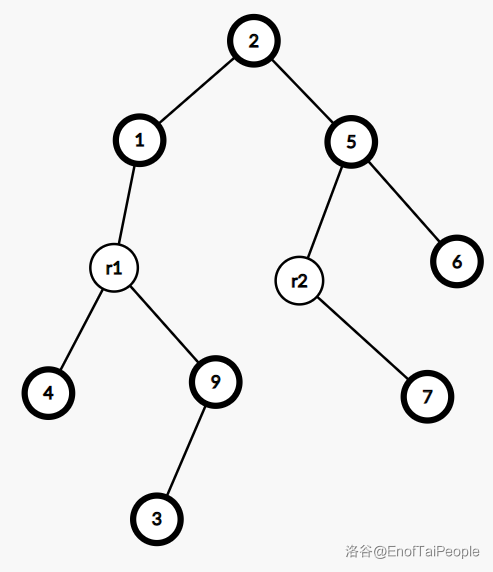
其中的 表示 ,其余表示 。
可以粗略理解为 维护实链, 维护虚儿子。
但这里 并没有和上方的 失去联系,而成为了 的中儿子。
在
pushdown时需要加给子树的标记会传给中儿子。在
pushdown时会给子树的两个标记都加上自己的标记。注意 只有一个标记,所以接受标记时也只有一个标记会用到。
可以简单理解成 是维护虚子树的 ,但如果只有一个虚儿子,唯一的 也会只有一个儿子。
任何时刻 都不会有中儿子。
access时只需要一次全局pushdown,因为任何一个节点都可以一次经过 和 到达根簇。遍历时只需要从根簇出发,遍历左右儿子和中儿子即可。
这样可以整体看作一棵大
splay,access时间复杂度为均摊 。由于只需要一次全局
pushdown,只有一棵树,常数相较 十分优秀,码量也很小。
Part4 其他做法
上面提到了两种做法是 的:虚子树 ,。
也有两种是 的: 和 。
你会发现,它们都是基于 的,所以时间复杂度都是均摊的。
假如你想要严格复杂度,
甚至可持久化。我们先考虑只要非暴力就行的方法。
注意:以下部分纯口胡,有错误可以直接指出。
- 每次打通最多增加 势能,所以可以每 次操作重构,注意这里需要重链剖分建全局平衡二叉树。
- 于是重构复杂度为 。
- 每次操作最多使用 势能。
- 总复杂度为 。
- 平衡一下取 ,总时间 。
否则你就不能使用势能了,而需要保证操作结束后保持严格重剖,具体地你需要将轻边抖落,重边连上,同时使用重量平衡树,注意这里使用
treap做到期望复杂度会相对好写。当然这个算法是暂时被我认为是考场不可写作的,注意 和 并不是。
Part5 后记
这道题可以被称作 的简单应用,事实上静态时的 划分结构也是 的良好性质,详见此文,于是这道题就真的成为 的简单应用了。
- 1
信息
- ID
- 4651
- 时间
- 4000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
