自动搬运

查看原文

来自洛谷，原作者为

	Daniel13265 **

搬运于2025-08-24 22:12:55，当前版本为作者最后更新于2019-11-10 01:07:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

$\text{Upd.}\ 06/02/2020.$ 更新了题面与题解。

$n\le10$

暴力枚举每条边的方向，然后判断每个点能到达的点记入答案即可。时间复杂度 $\mathcal O\left(2^n\times n^2\right)$。

$p=n-1$

树是一个菊花图。考虑到树的一条边连接的两个点一定会对答案产生一倍的贡献，所以单独计算。所以只需要将除了菊花图的中心的点以外的点分成两组，使两组的权值之和的积最大。由于这两组的权值和是固定的，所以只需要将这两组数分得尽量平均。使用 01 背包即可，时间复杂度 $\mathcal O\left(n\times a_i\right)$ 。

$p=2$

树是一条链。观察要求的式子：由于边被改为了单向边，因此 $\left[i\rightarrow j\right ]$ 与 $\left[j\rightarrow i\right ]$ 中最多只有一个为 $1$ 。如果所有边方向相同，那么可以保证对于所有的 $i$ 和 $j$ ，都有 $\left[i\rightarrow j\right ]+\left[j\rightarrow i\right ]=1$ 。此时一定能够取得最大值。直接计算即可。时间复杂度 $\mathcal O\left(n\right)$ 。

$p\le20$

考虑到**如果将一棵子树的所有边的方向全部翻转过来，整棵树内部产生的贡献是不变的。**然后我们就可以发现：分别以树的每一个结点为根，对于当前的根结点所有子结点，以这些结点为根的子树内部的边的方向分别与该结点与根结点的边的方向相同时产生的贡献的最大值就是答案。边的方向相同指两条边在以当前结点为根时均为由深度小的指向深度大的，或均为由深度大的指向深度小的。

画个图理解：

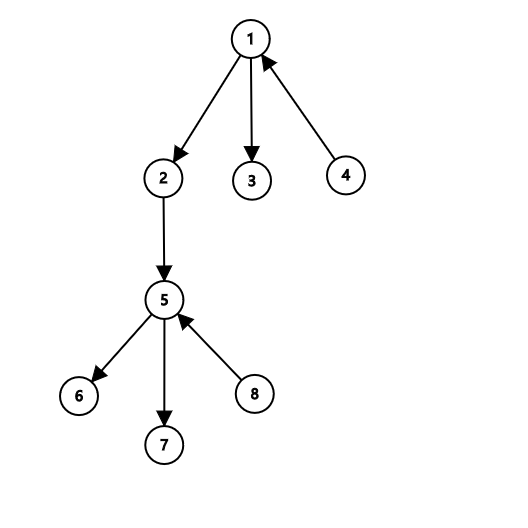
就是说，以 $1$ 号结点为根，那么在 $2,3,4$ 号结点所在的子树的所有边的方向分别相同时，可以得到多个解，取一个最优的。如果将以每个结点为根时得到的解再取最优值，就一定是答案。

举个例子：我们假设以 $1$ 号结点为根，并且连接 $5,8$ 号结点的边的方向不满足该结论。首先我们通过至多一次翻转操作将整棵树翻转一下使得 $5,8$ 号结点所在的子树的边的方向为从深度小的至深度大的。如果当前状态更优，就一定有 $a_6+a_7\ge a_1+a_2+a_4 >a_4$ 。如果存在这样的一个 $3$ 号结点使得连接 $1,3$ 号结点的边的方向像图中这样，那么会有 $a_4\ge a_2+a_5+a_6+a_7>a_6+a_7$ ，两者矛盾。所以此时一定就不存在这样的 $1,3$ 的连接方式。显然，这种情况会在以 $5$ 号结点为根时讨论到。

可以多举几个例子来说明这种看似错误的贪心算法其实是正确的，具体证明可以使用网络流建模，这里不再展开。

因此我们只需要枚举每个结点，再枚举每棵子树的方向，在求得的答案中取最大值即可。时间复杂度 $\mathcal O\left(n\times2^p\right)$，无法通过。

再考虑如果已经算出一个结点的答案，以及它的若干个子树分别的权值之和。那么可能更优的答案仅在它的权值之和最大的子树里，因为在权值之和小的子树中，包含原来的根结点的子树一定的权值之和一定会大于其余子树之和的一半，这样会使得将新的根结点的所有其他子树加起来没有原来的根结点所在的子树的权值大小大，答案一定不优。于是我们不断向加权后最大的子树转移即可。

因此我们只需要求出树的加权重心，直接计算以树的重心为根时的答案即可。时间复杂度 $\mathcal O\left(n+2^p\right)$ 。

$p\le40$

上面的算法时间复杂度劣在枚举各个子树的方向，即枚举每个数选或者不选。而如果像 $\text{subtask } 2$ 那样使用 $01$ 背包求解，会发现权值过大，因此我们需要找到一种更快速的解法。

观察到 $P\leq 40$ ，于是我们可以折半枚举，将前 $\left\lfloor\frac P2\right\rfloor$ 个数可能的和存入数组中排序，然后将后 $\left\lceil\frac P2\right\rceil$ 个数可能的和计算出来在之前的数组中二分查找即可。时间复杂度 $\mathcal O\left(n+2^{\frac p2}p\right)$，

无特殊限制

我们发现以上解法依旧很劣，因此我们需要继续优化。准确地，我们急需一种数据结构来维护一个集合，并能够支持快速地插入一个数与查找一个数的前驱后继。于是我们想到了这个，直接维护即可，具体实现请参考该题题解。时间复杂度 $\mathcal O\left(n+2^{\frac p2}\log_\omega{na_i}\right)$。