自动搬运

查看原文

来自洛谷，原作者为

	Foreverxxx Everything I need is on the ground.

搬运于2025-08-24 22:12:44，当前版本为作者最后更新于2021-11-03 14:33:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

update on 2021.12.17 修改了个别错别字。

广告：一名Blink的博客

首先感谢出题人 Inkyo 大佬，让我从这道题中学到了很多。

没有题解就让我来造福社会！

正文

题目传送门

做这道题之前，大家最好尝试一下这道题 P5633 最小度限制生成树，这对这道题很有帮助。

这道题一共有两步：

1、求一颗生成树，要求某个点 s 必须且只能向外连 $K$ 条边，同时满足最长边最短，次长边最短，以此类推。

2、对求出来的生成树，每次回答两个点的唯一路径的距离。

对于第二个问题，我们只需要在生成树上跑 LCA 就行了，重点是第一个问题，解决它需要一种新的生成树方式：最小度限制生成树。

关于最小度限制生成树的详解，可以参考我的另一篇题解： P5633 最小度限制生成树 题解

不过用我这种方法来建树是不合理的，因为它只能求出权值的和，却不能把树建出来。（其实是可以建的，不过很容易超时，大佬 AC 了当我没说）

所以我们需要转换思路。

可以考虑将 s 点分开，将其它的边单独考虑，具体想法如下：

假设在整张图中，节点 s 连了 $X$ 条边，那么在去掉 s 后，整张图会出现小于等于 $X$ 个连通块，而很明显每个块里面的连边情况不会对其它块以及节点 s 造成任何影响，因为加入节点 s 后，一定不会形成环。（实在没有理解的画画图吧）

所以我们可以将这些连通块单独进行处理，对每个块求出这个块的最小生成树，并且进行建边操作以便后面的询问。

现在问题来了，我们如何将节点 s 所需要的 $K$ 条边加入呢？

这里我们可以参考 P1315 观光公交 的思路，那道题是枚举每一个加速器，找到当前最需要的一个区间使用，我们观察这道题的数据范围： $1 \leq K \leq 150$ ，发现完全可以这样做，并且这样做是完全满足要求的！

对于样例而言，当我们对其进行连通块处理后，得到的图会是：

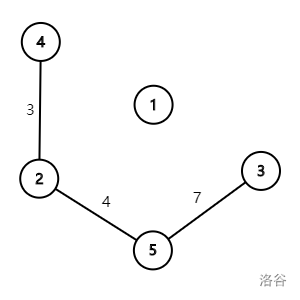
之后，我们需要的就是扫一次求出需要加入的边。

做到这里时我也卡住了，还是出题人教我怎么做的，感谢出题人。

我们可以发现，如果直接将 s 连的出边从小到大连起来，很可能会形成环，用并查集什么的维护是否是环也很困难，所以我们考虑用 dp 记录当时的情况。

我们用 dp 维护每个点到 s 的路径上最长边的权值和以及它的编号，那么状态转移方程就是：

$dp_{now} = \max (dp_{father},len_{now,father})$

用 DFS 搜索进行更新，搜索中同时维护编号即可。

最后，我们需要考虑什么时候会无解，有一下几种情况：

1、 s 点总共连出去的边不足 $K$ 条。

2、在搜索边时，还需要向 s 连边，不过已经没有可以连的边。

对于第二个问题，我使用的方法是倍增 LCA ，可能会被卡，不过问题不大。大家一起 Tarjan ！

计算方法也很简单：

$dist=dist_u+dist_v-2 * dist_{lca(u,v)}$

其中 dist 表示点到根节点的距离，如果不会请左转 P3379 【模板】最近公共祖先（LCA）

AC 代码

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
inline int read(){
	int sss=0;
	char chh=getchar();
	while(chh>'9'||chh<'0') chh=getchar();
	while(chh>='0'&&chh<='9'){
		sss=sss*10+chh-'0';
		chh=getchar();
	}
	return sss;
}
bool forever;
int n,m,k,s,q;
int ans=0;
struct node{
	int u,v,w;
};
int tot_s=0,tot_not=0,tot=0;
node edge_s[500005];
node edge_not[500005];
int fa[30005];
int fat[30005][16];
int Log[30005];
int depth[30005];
int dist[30005];
bool vis[500005];
bool cannot_use[500005];
int dp[500005];
int max_pos[500005];
int id[500005];
//前向星四件套 
int nxt[1000005];
int head[500005];
int val[1000005];
int to[1000005];
void add(int u,int v,int w){
	tot++;
	to[tot]=v;
    val[tot]=w;
    nxt[tot]=head[u];
    head[u]=tot;
    if(tot%2) id[tot]=tot+1;
    else id[tot]=tot-1;
}
bool cmp(node x,node y){
	return x.w<y.w;
}
int find(int x){
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
void Kruskal_union_block(){
	sort(edge_s+1,edge_s+tot_s+1,cmp);
	for(register int i=1;i<=tot_s;i++){
		int fau=find(edge_s[i].u),fav=find(edge_s[i].v);
		if(fau==fav) continue;
		/*
		在处理完与s无关的边后，仍然要保证连向s的边最小，否则形成的生成树不满足题意:
		要满足最长的电线尽量短，在此基础上还要满足次长的电线尽量短，以此类推。
		*/
		add(edge_s[i].u,edge_s[i].v,edge_s[i].w);
		add(edge_s[i].v,edge_s[i].u,edge_s[i].w);
		fa[fau]=fav;
		ans+=edge_s[i].w;
		//对已经连接的边进行标记 
		vis[i]=1;
		k--;//又连了一条边，s需要连出去的边的数量需要减一 
	}
}
void Kruskal_add(){
	sort(edge_not+1,edge_not+tot_not+1,cmp);
	for(register int i=1;i<=tot_not;i++){
		int fau=find(edge_not[i].u),fav=find(edge_not[i].v);
		if(fau==fav) continue;
		//细节处理
		/*
		在处理所有与s无关的点时，先求出若干个最小生成子树，可以证明不会出错
		因为这些边的联通情况与s点没有任何关系，所以要尽量保证取到权值小的边 
		*/ 
		//找到一条合法的边立即加入 
		add(edge_not[i].u,edge_not[i].v,edge_not[i].w);
		add(edge_not[i].v,edge_not[i].u,edge_not[i].w);
		fa[fau]=fav;
		ans+=edge_not[i].w;
	}
}
void dfs(int now,int father){
	/*
	最神奇的一段代码
	通过对目前已经连的边的DFS序
	找到最大的那条边进行删除操作
	时间复杂度o(n)级别
	和P1315 [NOIP2011 提高组] 观光公交有异曲同工之妙 
	即o(nk)的处理 
	每次扫一遍计算出需要的边 
	*/
	for(register int i=head[now];i;i=nxt[i]){
		//cout<<i<<"\n"; 
		int u=to[i],v=val[i];
		if(u==father) continue;
		if(cannot_use[i]) continue;
		if(now!=s){
            if(dp[now]>v) max_pos[u]=max_pos[now];
            else max_pos[u]=i;
            dp[u]=max(dp[now],v);
        }
        dfs(u,now);
	}
}
void init(int now,int father){
	depth[now]=depth[father]+1;
	fat[now][0]=father;
	for(register int i=1;i<=Log[depth[now]];i++)
		fat[now][i]=fat[fat[now][i-1]][i-1];
	for(register int i=head[now];i;i=nxt[i]){
		if(to[i]==father) continue;
		if(cannot_use[i]) continue;
		dist[to[i]]=dist[now]+val[i];
		init(to[i],now);
	}
}
int LCA(int x,int y){
	if(depth[x]<depth[y]) swap(x,y);
	while(depth[x]>depth[y])
		x=fat[x][Log[depth[x]-depth[y]]-1];
	if(x==y) return x;
	for(register int i=Log[depth[x]];i>=0;i--){
		if(fat[x][i]!=fat[y][i]){
			x=fat[x][i];
			y=fat[y][i];
		}
	}
	return fat[x][0];
}
int main(){
	n=read(),m=read(),k=read(),s=read();
	int uu,vv,ww;
	for(register int i=1;i<=m;i++){
		uu=read(),vv=read(),ww=read();
		if(uu==s||vv==s){//与s有连边 
			tot_s++;
			edge_s[tot_s].u=uu;
			edge_s[tot_s].v=vv;
			edge_s[tot_s].w=ww;
		}
		else { 
			tot_not++;
			edge_not[tot_not].u=uu;
			edge_not[tot_not].v=vv;
			edge_not[tot_not].w=ww;
		}
	}
	for(register int i=1;i<=n;i++) fa[i]=i; 
	/*
	必须先处理与s无关的边 
	保证最小生成子树最小
	否则先处理s会造成求得的生成树不满足题意 
	*/
	Kruskal_add();
	Kruskal_union_block();
	if(k<0){//如果将整张图变成一颗生成树，需要的边的数量必须大于K，这是不合法的情况 
		cout<<"can not fix it.";
		return 0;
	}
	while(k--){
		memset(dp,-INF,sizeof dp);
		dfs(s,0);
		int tmp_val=INF;
		int tmp_pos=INF,tmp_i=INF;
		int tmp_u=INF,tmp_v=INF,tmp_w=INF;
		//接下来枚举所有的连向s的边 
		for(register int i=1;i<=tot_s;i++){
			if(vis[i]) continue;//已经选择 
			int tmp_next_point;
			if(edge_s[i].u==s) tmp_next_point=edge_s[i].v;//找到这条边连出去的点 
			else tmp_next_point=edge_s[i].u;
			if(tmp_w>edge_s[i].w){//更新最小边 
				tmp_val=edge_s[i].w-dp[tmp_next_point];
				tmp_pos=max_pos[tmp_next_point];
				tmp_u=edge_s[i].u; 
				tmp_v=edge_s[i].v; 
				tmp_w=edge_s[i].w; 
				tmp_i=i;
			}
		}
		if(tmp_val>=1e8){//一共还没有K条边时就没有边可以连了 
			cout<<"can not fix it.";
			return 0;
		}
		add(tmp_u,tmp_v,tmp_w);//对找到的边进行连接 
		add(tmp_v,tmp_u,tmp_w);
		cannot_use[tmp_pos]=cannot_use[id[tmp_pos]]=1;
    	vis[tmp_i]=1;
    	ans+=tmp_val;
	}
	cout<<ans<<"\n";
	for(register int i=1;i<=n;i++) Log[i]=Log[i>>1]+1;
	init(s,0);
	q=read();
	while(q--){
		uu=read(),vv=read();
		cout<<dist[uu]+dist[vv]-2*dist[LCA(uu,vv)]<<"\n";
	}
	return 0;
}

至此，我们成功地过掉了此题，不过我们还可以有其它思考：

1、这种做法只能用前向星 （因为要记录边的状况），能不能用 STL 代替前向星呢？（其实是我自己通常都用的是来得快的 STL ）

2、能不能想出一种办法可以直接快速地求出当前能够接上的最小的边是哪条呢？

3、这道题到底能不能用 wqs 二分做呢？（我思考了半天认为可以实现，不过好像很有可能超时）

蒟蒻和大家一起进步中……