自动搬运

查看原文

来自洛谷，原作者为

	disangan233 ディストピア

搬运于2025-08-24 22:12:36，当前版本为作者最后更新于2019-11-03 23:43:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

算法一

考虑 $k=n$ 的情况，等价于求圆的面积并，可以用 Simpson 积分直接做。

也有另外一种方法。考虑题目圆心都在 $x$ 轴上且 $r$ 相等，直接计算每一个圆的新增面积即可。

具体做法为用 $\arcsin$ 求出扇形圆心角，减去三角形面积后即为相交面积的一半。

令 $d=2r-(x_i-x_j)$，$s(j,i)$ 为第 $j$ 个圆和第 $i$ 个圆的相交面积，所以可得：

$$s(j,i)=2r^2\arcsin{\frac{\sqrt{rd-\frac{d^2}{4}}}{r}}-(r-\frac{d}{2})\sqrt{4dr-d^2} $$

怎么样？这个式子是不是看着傻里傻气，又臭又长？考虑改进一下这个式子，采用向量叉积计算三角形面积即可。

$$\theta=2\arccos {\frac{d}{2r}}, s(j,i)=(\theta-\sin \theta)r^2 $$

可通过子任务 $1$，时间复杂度 $O(n)$ 或 $O(n\log n)$，期望得分 $11$ 分。

算法二

由 $n$ 选 $k$ 考虑 $dp$ 求解，令 $f_{i,k}$ 为前 $i$ 个圆选择 $k$ 个的最大面积并。

令 $S_0=\pi r^2$，可得出转移方程：

$$f_{i,k}=\max_{j<i} \{f_{j,k-1}+S_0-s(j,i)\}$$

暴力转移，时间复杂度 $O\left(n^2k\right)$ ，可通过子任务 $2$，结合算法一期望得分 $24$ 分。

发现对于 $x_i-x_j\geq 2r$ 的情况 $s(j,i)=0$，故可维护一个最大值优化转移。

时间复杂度 $O(nkr)$，可通过子任务 $2,3$，结合算法一期望得分 $30$ 分。

算法三

考虑子任务 $4$，因为数据随机生成，所以对于 $x_i-x_j<2r$ 的情况可以各种乱搞。

结合算法一、二，期望得分 $45$ 分。

算法四

发现 $S_0-s(j,i)$ 和 $(S_0-s(j,i))'$ 在 $[0,2r]$ 内单调递减，考虑决策单调性。

令 $f(x)=S_0-s(j,i)$ ，可以得到其二阶导数，发现其在定义域内恒为正，故 $f(x)$ 下凸。

$$f''(x)=\frac{(4r^2\sin\theta)\sqrt{4r^2-x^2}+2xr(\cos \theta-1)}{(4r^2-x^2)\sqrt{4r^2-x^2}} $$

显然这个二阶导数计算量极大，本答案采用 symbolab 验证通过。

这里采用 GeoGebra 画图的方法帮助验证，令 $f(2r-x_i+x_j)=S_0-s(j,i)$，有：

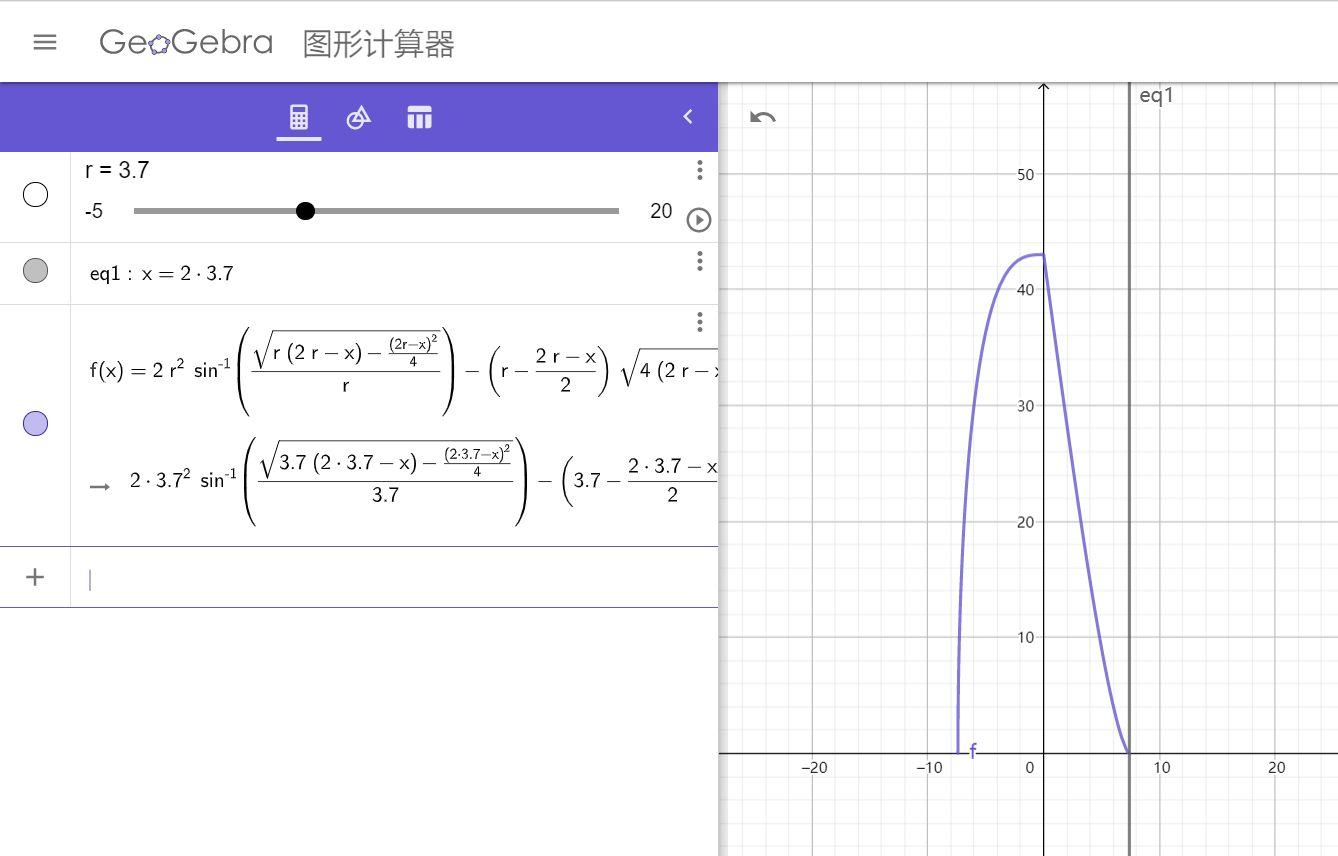
考虑 $\forall i<j$，令 $p_i,p_j$ 为 $i,j$ 的最优转移点，发现有 $p_i\leq p_j$。

采用反证法，假设 $p_i>p_j$，那么有 ：

$$f_{p_j,k-1}-s(p_j,i)\leq f_{p_i,k-1}-s(p_i,i),f_{p_i,k-1}-s(p_i,j)\leq f_{p_j,k-1}-s(p_j,j) $$

这个两个不等式同时取等时可以直接交换 $p_i,p_j$ ，考虑至少有一个取 $<$ 的情况，有：

$$f_{p_j,k-1}-s(p_j,i)\leq f_{p_i,k-1}-s(p_i,i),f_{p_i,k-1}-s(p_i,j)< f_{p_j,k-1}-s(p_j,j) $$

移项后得到：

$$s(p_i,i)-s(p_j,i)\leq f_{p_i,k-1}-f_{p_j,k-1},s(p_i,j)-s(p_j,j)> f_{p_i,k-1}-f_{p_j,k-1} $$

所以我们得到：

$$s(p_j,j)-s(p_j,i)<s(p_i,j)-s(p_i,i)$$

因为 $s'$ 在 $[0,2r]$ 内单调递减，且 $p_i>p_j$，所以发现上式不成立，故单调性得证。

另一种方法：显然 $s$ 满足四边形不等式，故得证。

因为 $s(j,i)$ 可以 $O(1)$ 计算，可以采用二分栈或者分治。

因为此处是导数递减，求 $\max$，已有的区间会对栈顶产生影响，故采用单调队列维护。

时间复杂度 $O(nk\log n)$，可通过子任务 $2-4,6$，结合算法一期望得分 $57$ 分。

算法五

发现 $f_{i,k}$ 的 $k$ 是凸的，考虑 wqs 二分优化 dp。

• 为什么是凸的呢，因为增量单调的性质可以转化为四边形不等式，所以得证。

对于每一个圆加上一个 $-mid$ 的权值，若选取的个数 $>k$ 则 $l=mid$。

时间复杂度 $O(nr\log r)$，可通过子任务 $2-5$，结合算法一期望得分 $68$ 分。

算法六

考虑将算法四和算法五相结合，可以强行结合，期望得分 $80$ 分。

发现分治做法会破坏 $f$ 更新的有序性，且只能针对上一维转移。

但是二分栈的做法满足了相对顺序，也不受上一维的限制，且 wqs 二分的切线函数为一次函数，其导数为定值，不会破坏转移方程的决策单调性。

所以将二分栈和 wqs 二分结合起来即可。

时间复杂度 $O(n\log n\log r)$，可通过所有子任务，期望得分 $100$ 分。

代码实现

#pragma GCC optimize(2,3,"Ofast","unroll-loops")
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define re register int
#define db double
#define in inline
namespace fast_io
{
    char buf[1<<12],*p1=buf,*p2=buf,sr[1<<23],z[23],nc;int C=-1,Z=0,Bi=0;
    in char gc() {return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<12,stdin),p1==p2)?EOF:*p1++;}
    in ll read()
    {
        ll x=0,y=1;while(nc=gc(),(nc<48||nc>57)&&nc!=-1)if(nc==45)y=-1;Bi=1;
        x=nc-48;while(nc=gc(),47<nc&&nc<58)x=(x<<3)+(x<<1)+(nc^48),Bi++;return x*y;
    }
    in db gf() {re a=read(),b=(nc!='.')?0:read();return (b?a+(db)b/pow(10,Bi):a);}
    in int gs(char *s) {char c,*t=s;while(c=gc(),c<32);*s++=c;while(c=gc(),c>32)*s++=c;return s-t;}
    in void ot() {fwrite(sr,1,C+1,stdout);C=-1;}
    in void flush() {if(C>1<<22) ot();}
    template <typename T>
    in void write(T x,char t)
    {
        re y=0;if(x<0)y=1,x=-x;while(z[++Z]=x%10+48,x/=10);
        if(y)z[++Z]='-';while(sr[++C]=z[Z],--Z);sr[++C]=t;flush();
    }
    in void write(char *s) {re l=strlen(s);for(re i=0;i<l;i++)sr[++C]=*s++;sr[++C]='\n';flush();}
};
using namespace fast_io;
const int N=1e5+5,R=1e4+5;
const db pi=acos(-1),eps=1e-9;
int n,k,nr,a[N],g[N],p[N],q[N];
db f[N],ans,cur,dat[R<<1],s0,mid;
in db s(re i,re j) {return (a[j]-a[i]>=2*nr)?0:dat[a[j]-a[i]];}
in int find(re i,re j) 
{
    re l=j,r=n+1,m; 
    while(l<r) {m=(l+r)>>1;(f[i]-s(i,m)<=f[j]-s(j,m))?r=m:l=m+1;}
    return l;
}
void dp(db mid)
{
    for(re i=1,h=0,t=0;f[i]=g[i]=0,i<=n;i++) 
    {
        while(h<t&&p[h]<=i) h++;
        f[i]=f[q[h]]+s0-s(q[h],i)-mid;g[i]=g[q[h]]+1;
        while(h<t&&p[t-1]>=find(q[t],i)) t--;
        p[t]=find(q[t],i);q[++t]=i;
    }
}
int main()
{
    n=read();k=read();nr=read();s0=pi*nr*nr;
    for(re i=0;i<2*nr;i++) {db tmp=2*acos(i/(2.0*nr));dat[i]=(tmp-sin(tmp))*nr*nr;}
    a[0]=-1e9;for(re i=1;i<=n;i++) a[i]=read();
    db l=0,r=s0;for(re i=1;i<=37&&r-l>5e-6;i++) {mid=(l+r)/2.0;dp(mid);(g[n]>k)?l=mid:r=mid;}
    printf("%.8lf\n",f[n]+(l+r)*0.5*k);
    return ot(),0;
}