自动搬运

查看原文

来自洛谷，原作者为

	Mubuky 如果结果不如你所愿，就在尘埃落定前奋力一搏。

搬运于2025-08-24 22:12:27，当前版本为作者最后更新于2019-10-28 07:04:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先，这道题显然和拓扑排序有关

知道了这一点，问题其实就解决了大半。

其次，读题后发现，题目要求求出 “最优情况” 和 “最劣情况” 两个答案

我们不妨在求解时将这两个问题分开。

对于“最优情况”，我们显然可以贪心的取编号最小的入度为$0$的点扩展。实现方式就是把拓扑排序的$queue$换成$priority\_queue(greater)$并维护一个变量$max$。按照题目中所描述的计分规则，我们已经获得了$40$分。

下面我主要讲“最劣情况”的求解。

对于“最劣情况”，能否再按照同上面方式的贪心(即把拓扑排序的$queue$替换为$priority\_queue(less)$)，答案是否定的，容易举出一组反例:

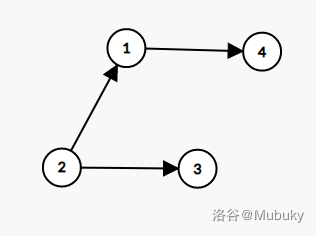
若按照先前的贪心，我们可以得到这样的一个扩展序列:

2 -> 3 -> 1 -> 4
ans = 3;

但存在这样一条扩展序列:

2 -> 1 -> 4 -> 3
ans = 2;

显然更优，这种解法出了问题，实际上这种解法加上“最优情况”的正解可以得到$46$分(实现方式差异可能会出现$52$分)。

那么如何求解呢？

我们看上面的反例，首先同拓扑排序找到入度为$0$的点(2)，此时max(之前走到的点的最大编号)为$0$且小于(2)，所以更新$max = 2$，更新答案$ans$++。

接下来待扩展的节点有2个，(1)和(3)，我们发现扩展(1)时答案($ans$)并不会增加，所以不妨先扩展(1)节点。

现在待扩展的节点是(4)和(3)，他们都大于max，都不能在答案不更新的前提下拓展。接下来不妨贪心的想，先拓展(4)再拓展(3)，即取编号最大的点先扩展。

#include<queue>
#include<cstdio>
#include<vector>
using namespace std;
int in2[500001];//入度
vector<int>g[500001];//存图
priority_queue<int,vector<int>,less<int> >qless;
queue<int>kz;//kz(queue)待扩展序列
int main()
{
	int maxn=0,ans=0;
	while(!qless.empty()){
		int x=qless.top();
		if(x>maxn){
			ans++;
		}
		while(!qless.empty()){
			kz.push(qless.top());
			qless.pop();
		}
		while(!kz.empty()){
			int nx=kz.front();
			kz.pop();
			maxn=max(maxn,nx);
			for(int j=0;j<g[nx].size();j++){
				int y=g[nx][j];
				in2[y]--;
				if(in2[y]==0){
					if(y>maxn){
						qless.push(y);
					}else{
						kz.push(y);
					}
				}
			}
		}
	}
	printf("%d",ans);
	return 0;
}

完整代码:

#include<queue>
#include<cstdio>
#include<vector>
using namespace std;
queue<int>kz;
priority_queue<int,vector<int>,greater<int> >qgreater;
priority_queue<int,vector<int>,less<int> >qless;
vector<int>g[500001];
int in[500001],in2[500001];
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		g[u].push_back(v);
		in[v]++;
		in2[v]++;
	}
	for(int i=1;i<=n;i++){
		if(in[i]==0){
			qgreater.push(i);
			qless.push(i);
		}
	}
	//"最优情况" 
	int maxn=0,ans=0;
	while(!qgreater.empty()){
		int x=qgreater.top();
		qgreater.pop();
		if(x>maxn){
			ans++;
		}
		maxn=max(maxn,x);
		for(int j=0;j<g[x].size();j++){
			int y=g[x][j];
			in[y]--;
			if(in[y]==0){
				qgreater.push(y);
			}
		}
	}
	printf("%d\n",ans);
	//"最劣情况" 
	maxn=0,ans=0;
	while(!qless.empty()){
		int x=qless.top();
		if(x>maxn){
			ans++;
		}
		while(!qless.empty()){
			kz.push(qless.top());
			qless.pop();
		}
		while(!kz.empty()){
			int nx=kz.front();
			kz.pop();
			maxn=max(maxn,nx);
			for(int j=0;j<g[nx].size();j++){
				int y=g[nx][j];
				in2[y]--;
				if(in2[y]==0){
					if(y>maxn){
						qless.push(y);
					}else{
						kz.push(y);
					}
				}
			}
		}
	}
	printf("%d",ans);
	return 0;
}

Update:感谢 @AxDea 和 @光明神 指出该篇题解样图分析中有关ans变量的问题