自动搬运

查看原文

来自洛谷，原作者为

	Provicy 这个家伙很懒，什么也没有留下

搬运于2025-08-24 22:12:25，当前版本为作者最后更新于2019-10-21 16:01:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$X-Round4 G$（提答题）

我可以负责任的告诉大家，以下内容基本为乱搞做法。

首先你需要一个可以画图的工具，推荐$GeoGebra$或几何画板之类的（反正我只会用这两个）。我此题用的是$GeoGebra$（没有几何画板）。

$Data1$：

显然题目让你$3$步求一个线段的中点，而且这两个点还在$x$轴上，作中垂线即可。

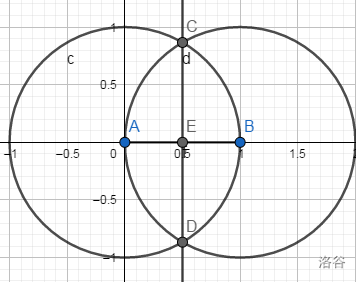
总结：第一个点还是很简单的，想必大家手算也能得出。

$Data2$：

显然，已知直线$AB$和直线外一点$C$，$3$步过$C$作$AB$的垂线。

已知$AB$，那么显然三步就可以作出这条垂线。

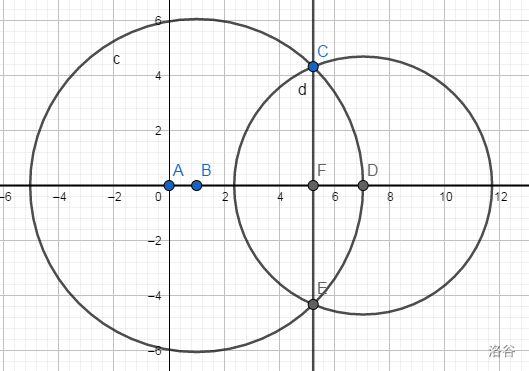
任取$A,B$其中一点为圆心，以$C$为圆上一点作一个圆，得到这个圆与$x$轴的右交点为$D$，再以$D$为圆心，$C$为圆上一点作一个圆，与第一个圆的一个交点显然为$C$，记另外一个交点为$E$。连结CE交$x$轴于$F$即为答案。

总结：还是不难，但需要少量几何功底。

$Data3$：

显然题目要求的是$5$步正方形内部一个三角形的外切圆的圆心。

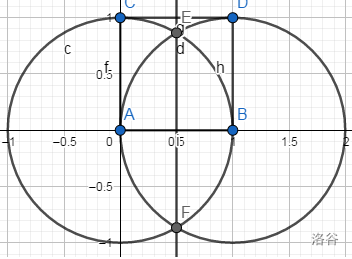
首先我们能得到上图的这个$3$步操作。这时候有人提出了个$6$步做法。。。

但我也不知道$6$步做法是什么，其实我们已经有一条$AB$的中垂线了，那么我们再作一条就行了。

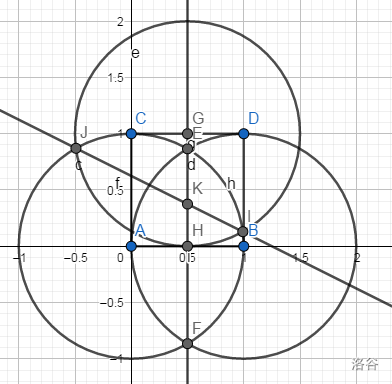
那么目标点就是△$ABG$的外心点$K$。

总结：这题只要看出目标点是正方形内某三角形的外心即可，难度不大。

$Data4$ && $Data5$：

（注意：无图！）

$Data4$要$10$步求点$(1024,0)$。由于$2^{10}=1024$，直接倍增求解即可。

$Data5$要$10$步求点$(1000,0)$。比起$Data4$稍要加些思考。

我们枚举其倍增后的二进制位然后考虑其和哪个点连边即可。经过各种尝试，我们还是通过把点$(128,0)$向$(4,0)$连边作圆以及把点$(504,0)$向$(8,0)$连边作圆即可得到点$(1000,0)$。注意，因为以上连边时这个圆半径比起$Data4$要小，故在后面的倍增求解中要持续减去这个数。

总结：这两个还是偏简单（比$Data2$和$Data3$还要简单），倍增求解即可。

$Data6$：

本人认为全场与$Data10$难度差不多的一个点。

给你一个圆，以及这个圆上任意一个点，去作一条直线与圆交于这个点。

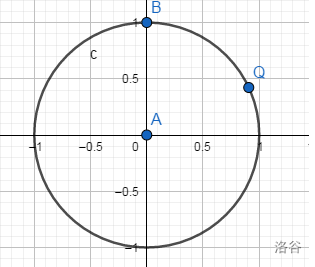
就是求$Q$这个点啦。

首先根据经验，我们会想到二分去求解。但事实证明二分需要$40+$次数，虽然也能拿到$9$分的好成绩，但还不是正解。

于是我们考虑用一条其中一个点为原点的直线去过这个点$Q$。

于是我们向$x$和$y$轴的正方向倍增枚举点，为了去逼近这个点，我们发现有时候把这个点连向$(0,1)$和$(1,0)$时更逼近答案。

一番瞎搞之后，我们还是能得出一个比较精确的点$(22049,10262.5)$

总结：这题较难，考查了枚举和乱搞的能力（说过了，这道题真的有点依靠乱搞水平，或许比爆搜还快不少）。

$Data7$：

纯考平面几何知识的一道题。

观察一段时间目标点之后，我们发现这题是求一个三角形的费马点。

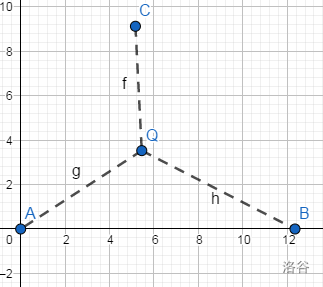
我们求一个三角形的费马点，如果这个三角形有一个内角大于等于$120$°，显然费马点就是这个顶点，否则就是到三边张角都是$120$°的角。

我们可以据此推出较简单的一种作法：

向△$ABC$外作等边三角形$ABA'$，再作其外接圆交$A'C$于$P$，则$P$就是费马点。

于是我们可以得到以下$3$步后的图形：

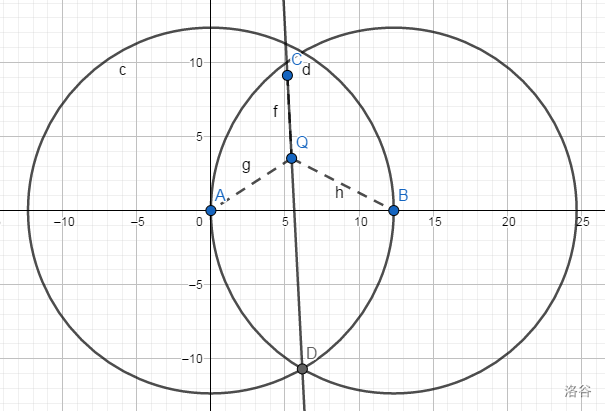
那么很快我们就有一种$6$步作法如下：

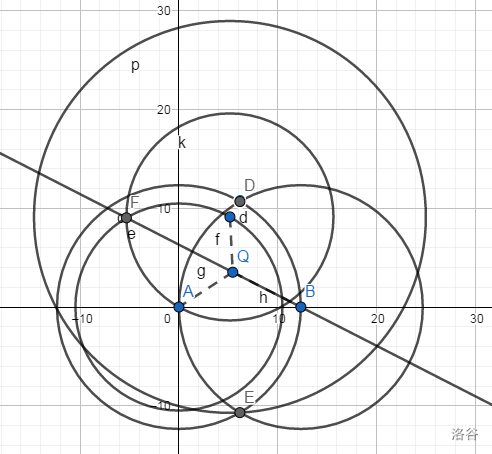
这是我考场上想到的作法，但是你是不是发现我在上上张图中有一条线在上张图中没有出现？

我们想到，我们不必要把这个等边三角形求出来，我们只需要知道这个$A'$在哪条直线上即可。

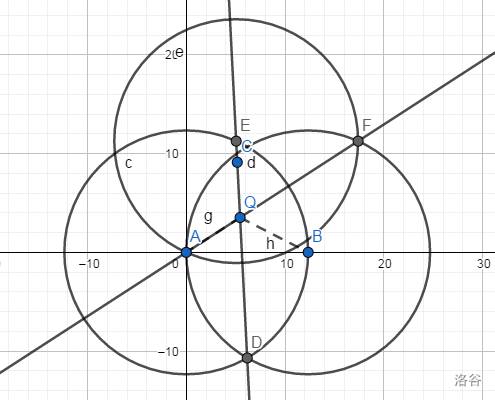
我们如此作三个圆之后，根据圆的性质，我们得到四边形$ABFE$为一个菱形。

作法：连结$CD$，交圆心为$A$的这个圆于$E$，那么以$E$为圆心，$A$为圆上一点作圆，交以$B$为圆心的圆于点$F$，连结$AF$。$AF$与$CD$交点即为点$Q$。

因为$EB$被固定，且根据$ABFE$是菱形的结论，我们得到$AF$为线段$BE$的中垂线。所以在直线$AF$上一定存在某点$P$，使得△$BEP$为等边三角形。则得到点$Q$。

总结：一道几何题，由$7$分向$10$分的突破是比较难的。

$Data8$：

和$Data7$提供的已知点相同，目标点也在由三个点组成的三角形内部，并且这三个点已经被组成一个三角形，于是我们猜想这个目标点是这个三角形的某心与某条边的切点。经检验，这个某心是该三角形的内心。

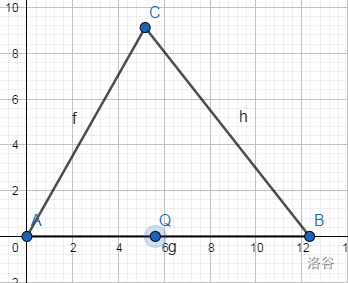
比起$Data7$的$5$步求费马点来说，这道题还是不难的。如果你对平面几何稍有了解，就知道如何快速求这个$Q$点。

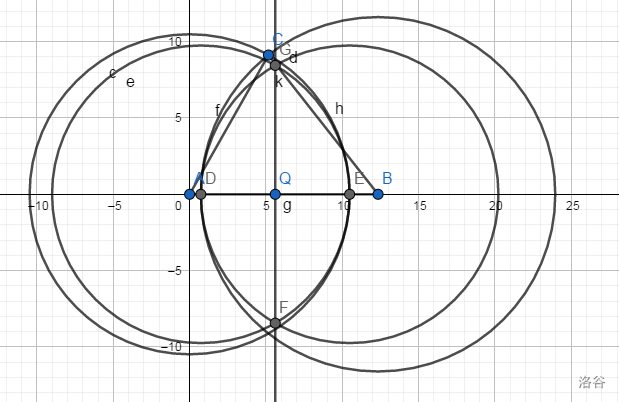
对这种中垂线构造如果熟悉的话这题没有难度。

总结：$Data6$到$Data10$中最简单的一题，也是考场上我在这$5$个点中唯一做出的点。

$Data9$：

还算容易的乱搞题。

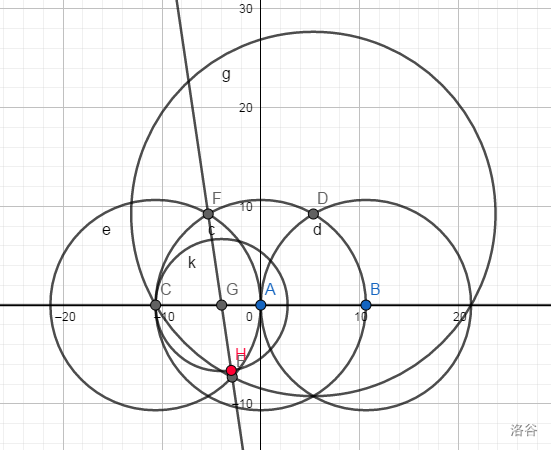
在直线$EF$上红点$H$即为所求。

我们观察到红点$H$与点$C$的关系，我们假设它们同为一个圆上的点，那么我们易想到存在$G$这个点，那么我们就要构造一条过$x$轴这个点的直线，我们对于几个圆的构造的尝试后得出以上图的结果。

总结：如果愿意去做这题，那么$Data9$就毫无难度，只需少数尝试即可。

$Data10$：

非常难的乱搞做法。

我们观察到$Data10$和$Data9$相比，给的步数变多了，同时这个点也离已知点较远，那么我们可以想到在$Data9$的基础上构造它。

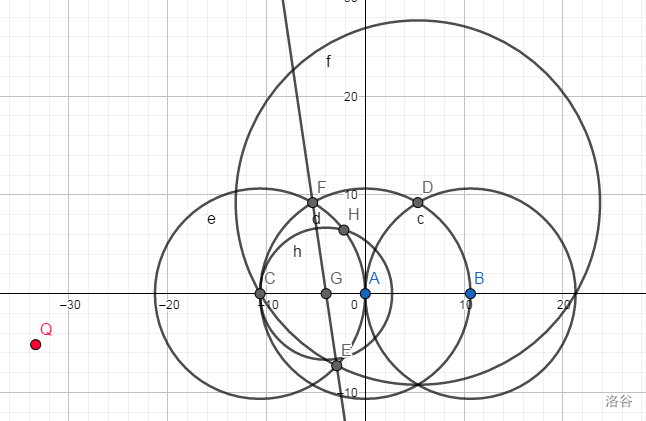
观察所求$Q$点，我们发现$Q$，$D$，$H$三点共线！我们大眼观察得到如此结论。于是根据这个特性，我们继续尝试构造。

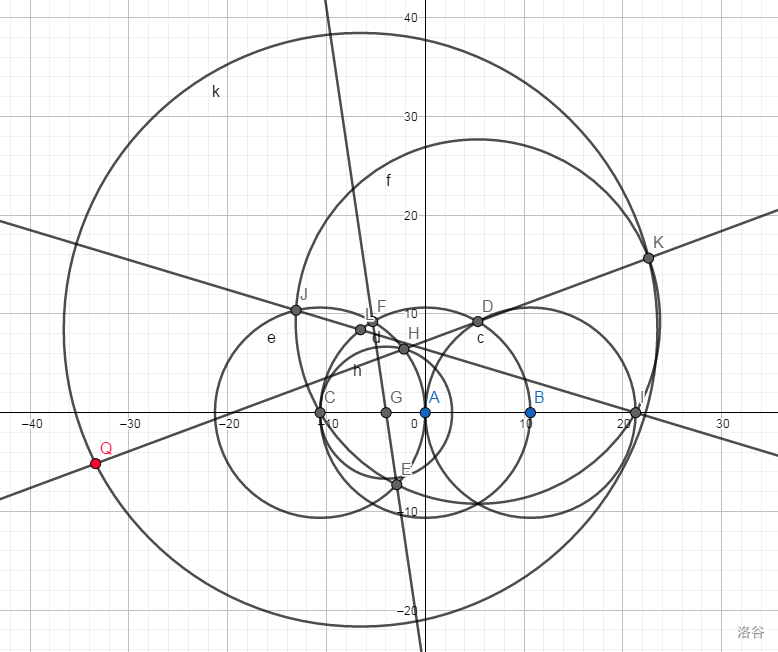
最终，我们的$Q$点以直线$HD$与以$D$为圆心的圆相交的右交点为圆上一点，以点$L$为圆心作圆，则得到$Q$，因为$Q$也在直线$HD$上。（乱搞出奇迹！）

总结：爆搜和乱搞都行的一个很难的点。但是我不会爆搜于是只能乱搞。

大总结：非常适合颓♂废的一道题，不过大家还是自己写比较好，也能比较好的锻炼几何感觉。

最后放下代码，各位可以对比对照一下（仅有答案），如果有更好的作法欢迎提出（$Data10$目前最短$9$步）：

#include <bits/stdc++.h>
using namespace std;

void BigPrint1()
{
	printf("40\n");
	printf("2 0 1 0 0\n");
	printf("1 0 1 0 -1\n");
	printf("1 0 -1 0 1\n");
	printf("2 -1.7320508075689 0 1.7320508075689 0\n");
	printf("1 0 1 0 0\n");
	printf("1 1 0 0 0\n");
	printf("1 2 0 1 0\n");
	printf("1 0 2 0 1\n");
	printf("1 3 0 0 0\n");
	printf("1 0 3 0 0\n");
	printf("1 6 0 1 0\n");
	printf("1 0 6 0 1\n");
	printf("1 11 0 0 0\n");
	printf("1 0 11 0 1\n");
	printf("1 22 0 0 0\n");
	printf("1 0 21 0 1\n");
	printf("1 44 0 1 0\n");
	printf("1 0 41 0 1\n");
	printf("1 87 0 1 0\n");
	printf("1 0 81 0 1\n");
	printf("1 173 0 1 0\n");
	printf("1 0 161 0 1\n");
	printf("1 345 0 0 0\n");
	printf("1 0 321 0 0\n");
	printf("1 690 0 1 0\n");
	printf("1 0 642 0 1\n");
	printf("1 1379 0 1 0\n");
	printf("1 0 1283 0 0\n");
	printf("1 2757 0 1 0\n");
	printf("1 0 2566 0 0\n");
	printf("1 5513 0 1 0\n");
	printf("1 0 5132 0 1\n");
	printf("1 11025 0 1 0\n");
	printf("1 0 10263 0 1\n");
	printf("1 22049 0 0 0\n");
	printf("1 0 20525 44098 0\n");
	printf("1 44098 0 0 20525\n");
	printf("2 4273.8285813547 -27927.4882594317 39824.1714159424 48452.4882592014\n");
	printf("2 0 20525 44098 0\n");
	printf("2 0 0 22049 10262.5\n");
}
void BigPrint2()
{
	printf("9\n");
	printf("1 10.64978745 0 0 0\n");
	printf("1 0 0 10.64978745 0\n");
	printf("1 -10.64978745 0 0 0\n");
	printf("1 5.324893725 9.2229864766047 -10.64978745 0\n");
	printf("2 -2.8891429892634 -7.293172854404 -5.324893725 9.2229864766047\n");
	printf("1 -3.9647169644197 0 -10.64978745 0\n");
	printf("2 -2.1668572419475 6.4387784412487 5.324893725 9.2229864766047\n");
	printf("2 21.2995749 0 -13.0855381857366 10.3675016799389\n");
	printf("1 -6.5503572407083 8.39707048614 22.6154412356748 15.6487848683712\n");
}
int main()
{
	int n; scanf("%d",&n);
	if(n==1) {printf("3\n1 0 0 1 0\n1 1 0 0 0\n2 0.5 0.8660254037844 0.5 -0.8660254037844\n"); return 0; }
	if(n==2) {printf("3\n1 1 0 5.23124577 4.31624417\n1 7.0442869307472 0 5.23124577 4.31624417\n2 5.23124577 4.31624417 5.23124577 -4.31624417\n"); return 0; }
	if(n==3) {printf("5\n1 0 0 1 0\n1 1 0 0 0\n2 0.5 0.8660254037844 0.5 -0.8660254037844\n1 0.5 1 0.5 0\n2 0.9916198487096 0.1291900756452 -0.4916198487096 0.8708099243548\n"); return 0; }
	if(n==4) {printf("10\n1 1 0 0 0\n1 2 0 0 0\n1 4 0 0 0\n1 8 0 0 0\n1 16 0 0 0\n1 32 0 0 0\n1 64 0 0 0\n1 128 0 0 0\n1 256 0 0 0\n1 512 0 0 0\n"); return 0; }
	if(n==5) {printf("10\n1 1 0 0 0\n1 2 0 0 0\n1 4 0 0 0\n1 8 0 0 0\n1 16 0 0 0\n1 32 0 0 0\n1 64 0 0 0\n1 128 0 4 0\n1 252 0 0 0\n1 504 0 8 0\n"); return 0; }
	if(n==6) {BigPrint1(); return 0; }
	if(n==7) {printf("5\n1 0 0 12.34441574 0\n1 12.34441574 0 0 0\n2 5.16457145 9.12243565 6.17220787 -10.6905776257165\n1 5.0557791797877 11.2616027654675 0 0\n2 0 0 17.4001949197877 11.2616027654675\n"); return 0; }
	if(n==8) {printf("5\n1 0 0 5.16457145 9.12243565\n1 12.34441574 0.00000000 5.16457145 9.12243565\n1 0.7354107775996 0 10.4829208930787 0\n1 10.4829208930787 0 0.7354107775996 0\n2 5.6091658353392 8.4415913836507 5.6091658353392 -8.4415913836507\n"); return 0; }
	if(n==9) {printf("6\n1 10.64978745 0 0 0\n1 0 0 10.64978745 0\n1 -10.64978745 0 0 0\n1 5.324893725 9.2229864766047 -10.64978745 0\n2 -5.324893725 9.2229846217 -2.8891429892634 -7.293172854404\n1 -3.9647169644197 0 -10.64978745 0\n"); return 0;}
	if(n==10) {BigPrint2(); return 0; }
	return 0;
}

后记：这算我写过最长的题解了吧，也是对这题比较详细的一个解答，希望大家能看懂，如果有不对的地方请指正$QwQ$