自动搬运

查看原文

来自洛谷，原作者为

	PineappleSummer 时光飞逝啊

搬运于2025-08-24 22:12:10，当前版本为作者最后更新于2023-08-24 11:22:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门

LCA 好题，细节挺多的，来写个题解吧。

首先分析样例，发现是这么一个图。

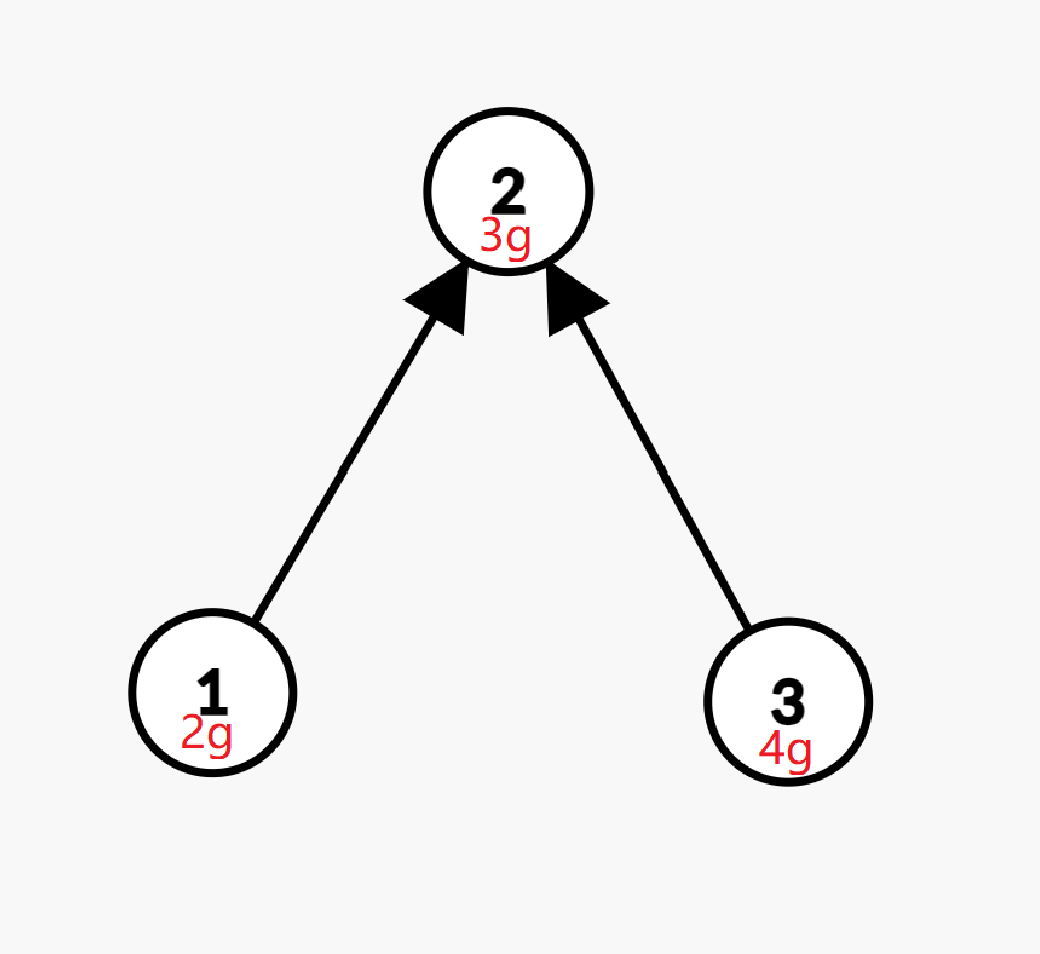
嗯，这不是仅仅图，这是树。题目上说：

第 $i$ 个步骤是将第 $a_i$ 个瓶子内的所有液体倒入第 $b_i$ 个瓶子，此后第 $a_i$ 个瓶子不会再被用到。

这不就是说一个儿子只能有一个父亲，而一个父亲可以有多个儿子吗？这不就是树？

建树。注意：应该把两个反应物向生成物连一条边，把 $b$ 自己拆成反应物和生成物，这样就可能会形成森林（不一定联通）。 此处感谢

建树代码：

for(int i=1;i<=m;i++)
{
	int u,v;
	cin>>u>>v;
	G[n+i].push_back(pos[u]);
	G[n+i].push_back(pos[v]);
	pos[v]=n+i;//pos[v]表示点v的生成物所在的点编号，初始化 pos[v]=v
}

我们进一步分析，发现对于可以进行反应的点对 $(u,v)$，如果 $(u,v)$ 有公共祖先（即有 LCA），他们就可能进行反应，反之则不可能进行反应。

预处理和倍增求 LCA 都是板子，这里就不放了，可以在最后的代码里查看。

for(int i=n+m;i>=1;i--)
	if(!d[i]) bfs(i);//图不一定联通
for(int i=1;i<=k;i++)
{
	int u,v;
	cin>>u>>v;
	int LCA=lca(u,v);//求LCA
	if(!LCA) continue;//没有公共祖先
	e[++tot]=Edge{u,v,LCA,d[LCA],i};//如果有，存入e结构体数组
}

$e$ 是一个结构体数组，其存储着每一对会发生反应的点对 $(u,v)$，其定义如下：

struct Edge
{
	int u,v,l,dep,id;//l为u,v的lca，dep为l的深度，id为反应的优先级
}e[K];

$e$ 数组是无序的，而反应是有序的，考虑对 $e$ 数组进行排序。先按照 $l$ 的深度从大到小排序，因为 $l$ 的深度越大，越早发生反应；$l$ 的深度相同的按照反应的优先级从大到小排序。

bool cmp(Edge a,Edge b)
{
	return a.dep>b.dep||(a.dep==b.dep&&a.id<b.id);
}

遍历每一个可以进行反应的点对 $(u,v)$，沉淀即为 $\min(g_u,g_v)\times 2$，$\min(g_u,g_v)$ 记为 $s$，用 $g_u$ 和 $g_v$ 分别减去 $s$，再拿 $ans$ 加上新增加的沉淀即可。

for(int i=1;i<=tot;i++)
{
	int s=min(g[e[i].u],g[e[i].v]);
	g[e[i].u]=max(0ll,g[e[i].u]-s),g[e[i].v]=max(0ll,g[e[i].v]-s);
	ans+=(s<<1);
}

最后输出 $ans$。

完整代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+10,K=5e5+10,logg=21;
int n,m,k,d[N],t,f[N][logg],pos[N],tot;
vector<int>G[N];
ll ans=0,g[N];
void bfs(int s)
{
	queue<int>q;
	d[s]=1;
	q.push(s);
	while(q.size())
	{
		int x=q.front();
		q.pop();
		for(auto i:G[x])
		{
			if(d[i]) continue;
			d[i]=d[x]+1;
			f[i][0]=x;
			for(int j=1;j<=t;j++)
				f[i][j]=f[f[i][j-1]][j-1];
			q.push(i);
		}
	}
}
int lca(int x,int y)
{
	if(d[x]>d[y]) swap(x,y);
	for(int i=t;i>=0;i--)
		if(d[f[y][i]]>=d[x]) y=f[y][i];
	if(x==y) return x;
	for(int i=t;i>=0;i--)
	{
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; 
	}
	return f[x][0];
}
struct Edge
{
	int u,v,l,dep,id;
}e[K];
bool cmp(Edge a,Edge b)
{
	return a.dep>b.dep||(a.dep==b.dep&&a.id<b.id);
}
int main()
{
//    freopen("input.in","r",stdin);
//    freopen("output.out","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m>>k;
	t=log2(n+m)+1;
	for(int i=1;i<=n;i++) cin>>g[i],pos[i]=i;
	for(int i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		G[n+i].push_back(pos[u]);
		G[n+i].push_back(pos[v]);
		pos[v]=n+i;
	}
	for(int i=n+m;i>=1;i--)
		if(!d[i]) bfs(i);
	for(int i=1;i<=k;i++)
	{
		int u,v;
		cin>>u>>v;
		int LCA=lca(u,v);
		if(!LCA) continue;
		e[++tot]=Edge{u,v,LCA,d[LCA],i};
	}
	sort(e+1,e+tot+1,cmp);
	for(int i=1;i<=tot;i++)
	{
		int s=min(g[e[i].u],g[e[i].v]);
		g[e[i].u]=max(0ll,g[e[i].u]-s),g[e[i].v]=max(0ll,g[e[i].v]-s);
		ans+=(s<<1);
	}
	cout<<ans;
    return 0;
}

如果觉得这篇题解写得好，请不要忘记点赞，谢谢！