自动搬运

查看原文

来自洛谷，原作者为

	WarningQAQ 私永遠に百鬼あやめが好きです

搬运于2025-08-24 22:12:02，当前版本为作者最后更新于2020-11-25 20:52:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

最近在刷平衡树，看到标题就进来了，没想到是个dp？？？看了看，发现可以贪心，于是就有了这篇题解。

分析：

因为红黑树本身的性质，所以我们可以通过画图来枚举所有情况：

先把每一个节点看成黑色的，通过红黑树性质来把一些结点变成红色的。

• $case1:$

如图：

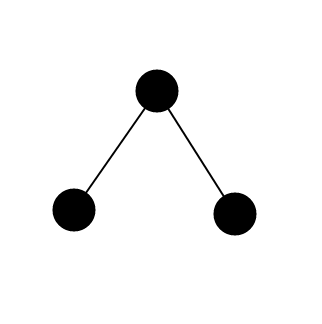
最亏的一种情况，两个黑色节点没变出来一个红色节点。

• $case2:$

如图：

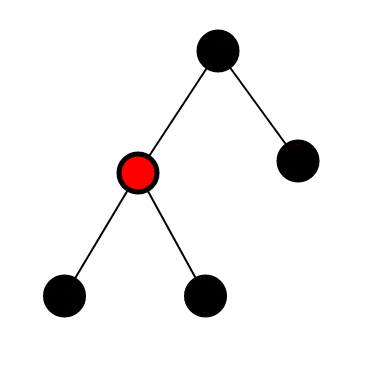
三个黑色节点变成一个红色节点，有点浪费。

• $case3:$

如图：

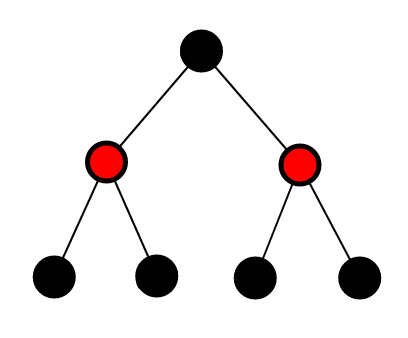
此时四个黑色节点变成两个红色节点，黑色节点的利用率最大。

所以，贪心就很明确了。

$\text{\large{code:}}$

#include "cstdio"
int n, ans, k;
int main()
{
	scanf("%d", &n);
	k = n + 1;
	while (k > 1)
	{
		ans += k & 1;
		k >>= 1;
	}
	printf("%d\n", ans);
	k = n + 1;
	ans = 0;
	while (k > 1)
	{
		if (k == 2)
			ans++, k--;
		else if ((k & 3) == 1)
			ans += ((k >> 2) << 1) - 1, k >>= 2, k++;
		else if ((k & 3) == 2)
			ans += ((k >> 2) << 1), k >>= 2, k++;
		else if ((k & 3) == 3)
			ans += ((k >> 2) << 1) + 1, k >>= 2, k++;
		else
			ans += (k >> 1), k >>= 2;
	}
	printf("%d", ans);
	return 0;
}

关于DP

自己想了一种方法，不过好像有亿点点慢。

以最小值为例：

用 $R_{(i,j)}$ 表示 $i$ 个结点，黑高度为 $j$ 的红根树中红色结点最小值；

$B_{(i,j)}$ 表示 $i$ 个结点，黑高度为 $j$ 的黑根树中红色结点最小值。

$\therefore R_{(i,j)}=\min\left({R_{(i,j)},B_{(k,j-1)}+B_{(i-k-1,j-1)}+1}\right)\quad(i\leq k\leq i-2)$；

$\therefore B_{(i,j)}=\min\left({B_{(k,j-1)},B_{(i-k-1,j-1)},R_{(k,j)}+R_{(i-k-1,j)},R_{(k,j)}+B_{(i-k-1,j-1)}}\right)\quad(i\leq k\leq i-2)$；

代码就不放了，贪心它不香吗？

$blog$