自动搬运

查看原文

来自洛谷，原作者为

	command_block 众水皆昂首，饮月唯我一。

搬运于2025-08-24 22:11:42，当前版本为作者最后更新于2021-07-05 23:44:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意 ： 给出平面上的一个点集 $S$ 。

给出平面上的若干个圆，对于每个圆，判定其是否完全在 $S$ 的凸包的内部。

保证圆的半径变化不超过 $1$ 时答案不发生变化。

$n,m\leq 5\times 10^5$，时限 $\texttt{2s}$。

将凸包拆分成上凸壳和下凸壳。我们只需分别判断圆是否在 上/下 凸壳内部。

下面只介绍上凸壳，将 $y$ 坐标翻转即可转化为下凸壳。

记 ${\rm convex}(S)$ 为点集 $S$ 的上凸壳（内部的区域）。

记 ${\rm contract}(T,r)$ 表示能完全放入平面区域 $T$ 中的半径为 $r$ 的圆的圆心的集合。

考虑随着 $r$ 的增大 ${\rm contract}\big({\rm convex}(S),r\big)$ 会如何变化。

若将 ${\rm convex}(S)$ 描述为半平面交，则变化相当于每个半平面缩小了 $r$ 单位距离。

在这个过程中，有些半平面可能不再在凸壳上，需要将其删除。

每个半平面只可能被两侧的半平面迫害掉，用堆维护每个半平面被迫害掉的时间。

如何计算 $l_1,l_3$ 迫害 $l_2$ 所需时间？

这是初中数学基础题：做两条角平分线，取交点到 $l_2$ 的距离。

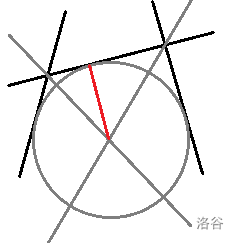
当某个半平面被删除时，重新计算两侧的半平面的迫害时间。

对于一个正确的收缩凸壳，容易二分判定圆心是否在其中。

用并查集维护序列，能支持删除某个元素，快速查找某个元素的前后继。

复杂度 $O\big((n+m)\log n\big)$。

代码常数很大。

#include<algorithm>
#include<cstdio>
#include<queue>
#include<cmath>
#define db double
#define MaxN 500500
using namespace std;
namespace io {
  char buf[5005000],*p1=buf,*p2=buf;
  #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,5000000,stdin),p1==p2)?EOF:*p1++)
  int rd() {
    int x=0;char ch=getchar(),f=0;
    while(ch<'0'||'9'<ch)f|=(ch=='-'),ch=getchar();
    while('0'<=ch&&ch<='9')x=x*10+(ch^48),ch=getchar();
    return f?-x:x;
  }
}using io::rd;
const db eps=1e-3;
struct Point{db x,y;}p[MaxN];
bool cmpP(const Point &A,const Point &B)
{return fabs(A.x-B.x)<eps ? A.y<B.y : A.x<B.x;}
Point operator + (const Point &A,const Point &B){return (Point){A.x+B.x,A.y+B.y};}
Point operator - (const Point &A,const Point &B){return (Point){A.x-B.x,A.y-B.y};}
Point operator * (const Point &A,db x){return (Point){A.x*x,A.y*x};}
Point operator / (const Point &A,db x){return (Point){A.x/x,A.y/x};}
db operator ^ (const Point &A,const Point &B){return A.x*B.y-A.y*B.x;}
bool anticlo(Point A,Point B,Point C){return ((A-B)^(C-B))>eps;}
db gl(Point A){return sqrt(A.x*A.x+A.y*A.y);}
struct Line{Point a,b;};
db dis(Line l,Point p){return ((p-l.a)^(l.b-l.a))/gl(l.b-l.a);}
bool chk(Line l,Point p,db r){return dis(l,p)+eps>r;}
Point dir(Line l){return (l.b-l.a)/gl(l.b-l.a);}
Line shift(Line l,db dis)
{
  Point d=dir(l)*dis;
  swap(d.x,d.y);d.y*=-1;
  return (Line){l.a+d,l.b+d};
}
Point inter(Line A,Line B)
{
  db sl=(A.a-B.b)^(B.a-B.b),sr=(B.a-B.b)^(A.b-B.b);
  return A.a+(A.b-A.a)*sl/(sl+sr);
}
db gr(Line A,Line B,Line C)
{
  Point p1=inter(A,B),p2=inter(B,C);
  Line l1=(Line){p1,p1-dir(A)+dir(B)}
      ,l2=(Line){p2,p2-dir(B)+dir(C)};
  return fabs(dis(B,inter(l1,l2)));
}
struct Cir{Point o;int r,p;}s[MaxN];
bool cmpC(const Cir &A,const Cir &B){return A.r<B.r;}
int f[MaxN],c[MaxN];
int find(int u)
{return f[u]==u ? u : f[u]=find(f[u]);}
void merge(int u,int v){
  u=find(u);v=find(v);
  c[f[u]=v]+=c[u];
}
Line l[MaxN];db dt[MaxN];
#define Pr pair<db,int>
#define fir first
#define sec second
#define mp make_pair
priority_queue<Pr,vector<Pr>,greater<Pr>> q;
int nowr,top;
void upd(int p)
{
  if (p==1||p==top)return;
  db ndt=gr(l[find(p-1)],l[p],l[p+c[p]]);
  if (dt[p]-ndt>eps)q.push(mp(dt[p]=ndt,p));
}
void del(int p){
  merge(p,p-1);p=find(p);
  upd(p);upd(p+c[p]);
}
bool qry(Point p)
{
  int tl=2,tr=top-1;
  while(tl<tr){
    int mid=(tl+tr+1)>>1;
    int t=find(mid);
    if (t==1){tl=mid+1;continue;}
    int pre=find(t-1);
    if (inter(shift(l[pre],nowr),shift(l[t],nowr)).x<p.x+eps)tl=mid;
    else tr=mid-1;
  }return tl<=1||tl>=top||chk(l[find(tl)],p,nowr);
}
Point stk[MaxN];
int n,m,tn;
bool ans[MaxN];
void calc()
{
  top=0;
  for (int i=1;i<=n;i++){
    while(top>1&&!anticlo(stk[top-1],stk[top],p[i]))top--;
    stk[++top]=p[i];
  }
  top--;
  for (int i=1;i<=top;i++){
    l[i]=(Line){stk[i],stk[i+1]};
    f[i]=i;c[i]=1;
  }
  while(!q.empty())q.pop();
  for (int i=2;i<top;i++)
    q.push(mp(dt[i]=gr(l[i-1],l[i],l[i+1]),i));
  for (int i=1;i<=m;i++){
    nowr=s[i].r;
    while(!q.empty()&&q.top().fir+eps<nowr){
      Pr now=q.top();q.pop();
      if (now.fir-dt[now.sec]>eps)continue;
      del(now.sec);
    }
    ans[s[i].p]&=chk(l[1],s[i].o,nowr);
    ans[s[i].p]&=chk(l[top],s[i].o,nowr);
    if (ans[s[i].p])ans[s[i].p]&=qry(s[i].o);
  }
}
void solve()
{
  n=rd();
  for (int i=1;i<=n;i++){p[i].x=rd();p[i].y=rd();}
  sort(p+1,p+n+1,cmpP);
  m=rd();
  for (int i=1;i<=m;i++){
    s[i].o.x=rd();s[i].o.y=rd();s[i].r=rd();
    ans[s[i].p=i]=1;
  }sort(s+1,s+m+1,cmpC);
  calc();
  for (int i=1;i<=n;i++)p[i].y*=-1;
  for (int i=1;i<=m;i++)s[i].o.y*=-1;
  calc();
  for (int i=1;i<=m;i++)putchar(ans[i] ? '1' : '0');puts("");
}
int main()
{
  int T=rd();
  while(T--)solve();
  return 0;
}