自动搬运

查看原文

来自洛谷，原作者为

	yyh_1102 **

搬运于2025-08-24 22:11:38，当前版本为作者最后更新于2019-08-27 22:14:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

青原樱/wa,好有诗意的题目/

• 首先，感谢银临为我们提供的NOIP模拟赛/话说NOIP改名了/

• 本篇文章为萌新oier而做，dalao及神犇绕路

• 废话不多说，这道题考察的是排列组合中的插空法，我先分析一下题目：一共有n个位置，m棵树，两棵树之间要有空位

  那么，我们把这m棵树以及他们所占的位置拿出来，那道路上是不是还剩下n-m个坑，而这n-m个坑有n-m+1个空位，我们要把带坑的树插进这n-m+1个空位中，那么有多少种插法？

  ans=$A^m_{n-m+1}$

  因为树是有序的，所以是A而不是C

  什么？你不明白A,C怎么算？

  • $A^m_n$=$n(n-1)···(n-m+1)$=$\frac{n!}{(n-m)!}$

  • $C^m_n$=$\frac{A^m_n}{m!}$=$\frac{n!}{m!(n-m)!}$=$C^{n-m}_n$

• A是排列数，C是组合数，那么什么叫排列，什么叫组合呢？

  所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序，是有序的。

  组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序，是无序的，这就是为什么$C^m_n$=$\frac{A^m_n}{m!}$的原因，当有序的排列除去顺序后就是组合。

  这里有个特殊规定，$0!=1$,怎么理解呢，通过上面的式子我们可以知道$A^m_n$表示在n个元素中有序的选取m个元素，当m=n的时候，$A^n_n$=$n!$，那么$0!$=$A^0_0$，从0个元素中有序地选出0个元素的方案数，应该只有一个，所以$0!$=1.

• 举个栗子吧,老师从十个人中选五个排成一列，一共有多少种排法？

  首先我们看，十个人中选五个排成一列的组合数是$C^5_{10}$，那么排成一列的同学们有没有顺序呢？

  答案是肯定的，你可以这么想，第一个人你给他1wRMB，第二个人你给他1w美刀，第三个人你给他1w欧，第四个人你给他1w津巴布韦币，第五个人你给他一巴掌，这待遇能一样吗，不同的排序结果能一样吗，既然不一样，那就是有顺序的，所以还要对组合数乘上一个5的全排列，答案是

  $C^5_{10}$×$A^5_5$=$A^5_{10}$=$10×9×8×7×6$=$30240$种

  这是一道简单的排列题，下面我们再来看一道组合题：老师从十个人中选取4个人去乡村支教，一共有多少种选法？

  我们看这道题有没有顺序，比如$a_1$到$a_{10}$十个人，老师选$a_1,a_2,a_3,a_4$去和选$a_4,a_3,a_2,a_1$去有区别吗，都是这四个人去，没有区别，所以这道题是无序的。无序的就是组合数，答案是

  $C^4_{10}$=$\frac{10!}{4!×(10-4)!}$=$210$种

  经过这两道例题，想必大家对排列组合有了一定的了解，下面开始讲一些比较难的题目了

  例一：三个女生和五个男生站成一排

  (1)如果女生必须全排在一起，有多少种排法？

  (2)如果女生必须全分开，有多少种排法？

  (3)如果两端都不排女生，有多少种排法？

  (4)如果两端不都排女生，有多少种排法？

  首先看第一题，所有女生全部都在一起，我们可以把女生全部绑在一起（某些绅士不要想歪），把三个女生看成一个女生，这样就成了一个女生，五个男生，一共有多少种排法。

  这是个排列问题，所以是有序的，一个女生五个男生的排法数是$A^6_6$种，又因为三个女生的顺序也是需要考虑的，所以答案还要乘上一个$A^3_3$，最后答案是

  $A^6_6 × A^3_3 = 6! × 3! = 4320$种

  这是第一题，下面看第二题，如果女生必须分开，有多少种排法，这就是不相邻问题，跟本题青原樱是一样的，使用插空法。我们看一共有五个男生，那连头带尾的算一共有六个空位，这里我简单表示一下，用@表示男生，用__表示空位

  __ @ __ @ __ @ __ @ __ @ __

  是不是六个空位，然后把三个女生插入这六个空位（再次警告绅士们不要想歪）中，由于三个女生的排列是有序的，所以女生排列的方案数是$A^3_6$，但这道题不是种树，男生的顺序也是要考虑的，所以最后答案是

  $A^3_6 × A^5_5 = 14400$种

  第二题是不相邻问题，我们一般对不相邻问题进行插空法解决问题，看第三题，两端都不排女生，意思是女生只能在中间6个位置中进行排列，由于是有序的，方案数是$A^3_6$，然后对剩余的五个男生进行排序，由于八个位置女生已经占了三个，所以还剩五个位置，男生排序又是有序的，所以答案是

  $A^3_6 × A^5_5 = 14400$种

  你们有没有发现答案跟上一题一模一样，这样不好分辨，我们还有另外一种方法，我们可以这样想，两端不能排女生，所以两端只能排男生，这个的方案数是$A^2_5$，然后再对剩下六个位置六个人进行排序$A^6_6$，最后把两个相乘就是答案

  $A^2_5 × A^6_6 = 14400$种

  答案是一样的，所以一道题可能有不同的表示方法，关键在于你怎么想，看第四题，要求女生不都在两端，这就和第三题不一样了，要求女生不都在两端，说明可以有一个女生在前端或后端，我们可以这样考虑，如果首位排的是男生，那么后面就不再有限制，然后对后面七个位置排序就行，首位男生的方案数是$A^1_5 ×A^7_7$种，再想，如果首位是女生，那么最后一位肯定是男生，然后对剩余六个人六个位置进行排序即可，方案数是$A^1_3 \times A^1_5 \times A^6_6$种，最后把两个方案相加就是最终答案

  $A^1_5 \times A^7_7 + A^1_3 \times A^1_5 \times A^6_6 = 36000$种

  还有第二种方法，就是从所有排列方案种把两端都是女生的方案全部扣下来，就是最终方案

  $A^8_8 - A^2_3 \times A^6_6 =36000$种

  经过了例题一的洗礼，你是否对排列组合已经有了初步的了解，那么一起来看例题二吧

  例二：排一张有5个歌唱节目和4个舞蹈节目的演出节目单。

  （1）任何两个舞蹈节目不相邻的排法有多少种？

  （2）歌唱节目与舞蹈节目间隔排列的方法有多少种？

  看第一题，任何两个舞蹈节目不相邻，是不是跟例一的第二题一样，使用插空法，五个歌唱节目有六个空，又因为节目的排列是有顺序的，所以答案是

  $A^4_6 \times A^5_5 =43200$种

  对舞蹈排序，对歌唱排序，最后相乘就是结果，难度不大，看第二题，歌唱节目和舞蹈节目间隔排列的方法数，这道题可以这样想，先把舞蹈节目排好有$A^4_4$种方案，再观察一下，四个舞蹈节目正好有五个空供五个歌唱节目插入，所以答案再乘上$A^5_5$就行了，最后答案是

  $A^4_4 \times A^5_5 = 2880$种

  例题二的第二题需要一点技巧，但也不算太难，我们再做几题巩固一下吧

  例三：某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课，如果第一节不排体育，最后一节不排数学，那么共有多少种不同的排课程表的方法？

  这道题不同于之前的题，复杂度变大了一点，我们看一下这道题：一共六节课，要求第一节课不排体育，最后一节课不排数学，我们直接想是不是很难想到方案，那么这里要用到一个概念：正难则反。

  正难则反的意思是如果顺着题目意思很难想出答案，那么就跟他反着来，他不是问第一节不是体育，最后一节不是数学的方案数吗，我们就求第一节是体育和最后一节是数学的方案总数，最后用总方案数减去这个方案数就是最后答案。

  我们可以看一下，第一节是体育的方案是$A^5_5$种，就是把体育排好，剩下五门课的全排列，数学同理，也是$A^5_5$种，两个相加是$2A^5_5$种，你以为这就是答案？

  少年啊你太天真了，你难道没有发现这里面有重复的方案吗，两个$A^5_5$都包括了体育第一节，数学最后一节，其他四门放中间的方案数，等于这一块算了两遍，所以我们要减去一遍这种方案，数学体育固定好了，中间四门课的方案数是$A^4_4$种，所以体育第一节，数学最后一节的总方案数是$2A^5_5-A^4_4$，再用总数减去方案数，最后答案是

  $A^8_8-(2A^5_5-A^4_4) = 504$种

  最后再看两题吧

  例四：现有3辆公交车、3位司机和3位售票员，每辆车上需配1位司机和1位售票员．问车辆、司机、售票员搭配方案一共有多少种？

  这道题我们可以分步骤进行排列，把三个司机分到三辆车上的方案数有$A^3_3$种，把三个售票员分到三辆车上的方案数有$A^3_3$种，所以最后答案是

  $A^3_3 \times A^3_3 = 36$种

  最后看一下例五吧

  例五：下是表是高考第一批录取的一份志愿表．如果有4所重点院校，每所院校有3个专业是你较为满意的选择．若表格填满且规定学校没有重复，同一学校的专业也没有重复的话，你将有多少种不同的填表方法？

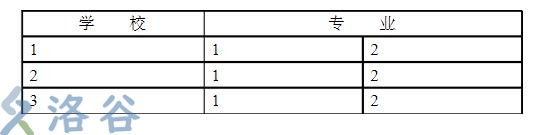
  我们可以看出来这道题的难度大大提升，所以我们要冷静分析，首先，志愿只能填三个学校，所以学校的方案数是$A^3_4$种，再分析专业，每个学校有三个专业是我满意的，但只能填两个专业，所以是$A^2_3$种，由于有三个学校 所以专业的排列数有$A^2_3 \times A^2_3 \times A^2_3$种，最后分步相乘，得出最终答案

  $A^3_4 \times A^2_3 \times A^2_3 \times A^2_3 = 5184$种

  例五这种比较复杂的题要分步考虑，冷静分析，把复杂的大问题拆成简单的子问题，然后再对子问题进行相乘或相加就是最后的答案

• 总结

• 排列组合的经典例题我挑了几题来讲，可以说足够你们排列组合入门了，而且一般考试题都能做对，至于还有没有我没有讲到的题型？肯定是有的，但这要靠你自己去探索，我能做的就只有这么多了。

最后奉告一句，凡事都要仔细，冷静，写题也是一样，不管是数学还是oi，能拿高分靠的都是仔细看题，冷静分析，所有的难题都是靠一个一个简单的问题堆积起来的，只要你能够把这些简单的问题拆开，那所谓的难题对你来说就没有难度了。

至于这道题的代码我就不放了，上面的大佬都有，我主要是为了给萌新们普及排列组合的知识，可能有问题，希望大佬们找到问题后评论出来，让我及时纠正。

看在这么有诗意的题目名称及背景上，我写了一首打油诗来帮助你们记忆排列组合的方法，同时也作为这篇题解的结尾

       ‘A’‘C’基础全排列，相邻捆绑反插空

        正难则反思维逆，复杂问题细分析

             常言道排列组合问题难

               我偏把难题拆分开

               欲问过程如何写

               加减乘除全‘A’‘C’