自动搬运

查看原文

来自洛谷，原作者为

	RiverFun 纱路酱实在是太可爱了~

搬运于2025-08-24 22:11:35，当前版本为作者最后更新于2019-08-24 16:48:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

广告：我的BLOG

部分分很好拿，我就直接讲正解吧。

前置知识：导数

你需要了解导数的含义和一些初等函数的导数。

让我们先来用几何画板模拟一下这个题中的一个函数。

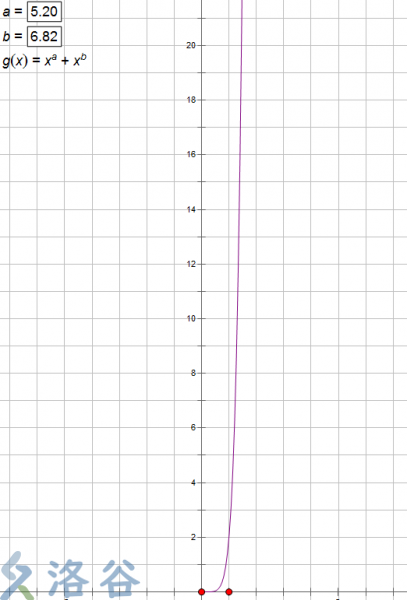
我们会发现如果 $a,b$ 都在所归定的数据范围内，这个函数图像形状很像二次函数，并且这个函数增长速度非常快。

我们设满足题意的最小 $n'$ 为 $a_1$ ，满足题意的最大 $n'$ 为 $a_2$。

所以 $f(a_1) - f(a_2) < 1$

我们可以任取两个 $f(a_1),f(a_2)$ 来观察一下。

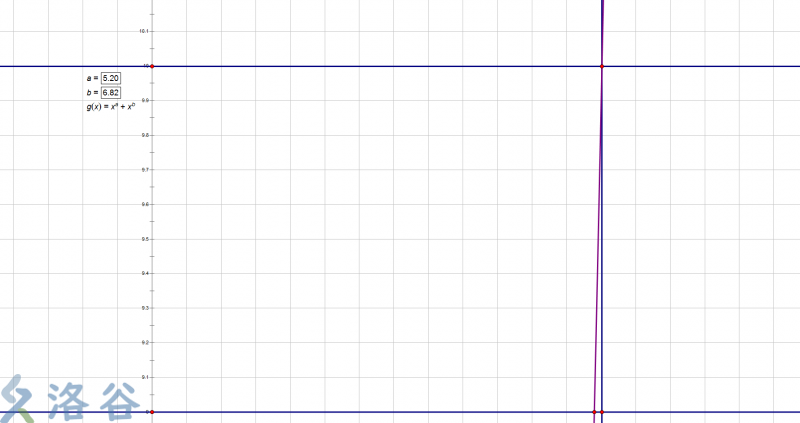
又可以发现这几个点围成了一个三角形的图案。

可能这时候有人会说：函数图像明明是曲线啊，怎么可能会是直线呢？

是的，确实是曲线，但是，用题目中所给的数据计算的话，得出的答案很大，已经到了可以忽略曲率的地步，并且题目要求的精度也不高，所以我们能够直接把这段函数图像看成直线。

但是为题又来了，该如何求它的斜率呢？

这时候，我们就需要用到导数了！

因为导数所求的是在函数任意一点处的斜率，而又因为 $f(n)$ 一定在这段函数图像上，所以我们可以直接把 $f'(n)$ 当做这个三角形斜边的斜率。

最后就可以得出答案 $a_2 - a_1 = \frac{0.999}{f'(n)}$。

上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
namespace Mker {
#define uint unsigned int
	uint sd;
	int op;
	inline void init() {
		scanf("%u %d", &sd, &op);
	}
	inline uint uint_rand() {
		sd ^= sd << 13;
		sd ^= sd >> 7;
		sd ^= sd << 11;
		return sd;
	}
	inline double get_n() {
		double x = (double) (uint_rand() % 100000) / 100000;
		return x + 4;
	}
	inline double get_k() {
		double x = (double) (uint_rand() % 100000) / 100000;
		return (x + 1) * 5;
	}
	inline void read(double &n,double &a, double &b) {
		n = get_n();
		a = get_k();
		if (op) b = a;
		else b = get_k();
	}
}
using namespace Mker;
int T;
double n, a, b, k, ans;
int main() {
	scanf("%d", &T);
	init();
	while (T--) {
		read(n, a, b);
		k = a * pow(n, a - 1) + b * pow(n, b - 1);
		ans += 0.9999999 / k;
	}
	printf("%0.5f", ans);
}