15011418730 LV 7 @ 2025-8-24 22:11:32

自动搬运

来自洛谷，原作者为

	Hope2075 时间的流沙，淹没梦境里的夏

搬运于2025-08-24 22:11:32，当前版本为作者最后更新于2019-08-13 21:58:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

2020/12/28:更新块状链表的时间复杂度分析

注：出题人表示，树套树的复杂度分析比较困难

~~听说有人用玄学做法水过去了，还有不少人用暴力得了不少分~~

话说最后一行的"不保证数据随机"有人看到了吗QWQ

出题人本来想卡块状链表，但是树套树跑得很慢，而且太容易MLE了，所以最后决定都放过去

算法1

纯暴力，按照题意模拟

时间复杂度 $O(nm)$ ,空间复杂度 $O(n)$

期望得分：4分

当然大力卡常能过#2和#3

算法2

针对#2

发现 $h$ 只能是0或1

于是可以用一个线段树，维护区间赋值和区间求和

时间复杂度 $O(m \log n)$ ,空间复杂度 $O(n)$

期望得分：14分

结合算法1期望得分：18分

算法3

针对#2 #5

#5的区别是强制在线，而且 $n$ 范围特别大

所以和算法2基本相同，动态开点就可以

时间复杂度 $O(m \log n)$ ,空间复杂度 $O(m \log n)$

期望得分：26分

结合算法1期望得分：30分

算法4

考虑算法3的缺陷

如果能维护很多数，那么就能AC

这时发现维护一个线段树就不行了

画一个这样的图（这是样例最后一次修改后的情况）

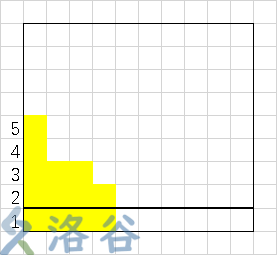
可以看出，每次操作可以转化为二维平面上区间赋值，询问可以转化为区间求和

可以用二维线段树维护

不过直接开空间肯定开不下，所以需要动态开点

时间复杂度 $O(m\log^2n)$ ，空间复杂度 $O(m\log^2 n)$

时间复杂度较小，而且常数不太大，但空间开销相当大，有MLE风险

期望得分100分，但很有可能被MLE卡成51分甚至更低

~~出题人并不会写二维线段树，所以没试过~~

算法5

针对#6

发现先修改后询问

所以，考虑先求出修改后的情况，再处理询问

处理修改的情况时，可以用动态开点线段树维护（当然这个点不强制在线，也可以离散化）

处理完后，发现就是静态区间求某数排名

然后可以用主席树/树套树完成剩下的部分

用树套树就基本是板子了，可以参考模板题的题解

用主席树：

按照数字从小到大，依次在线段树上进行区间赋值为1的操作，保留历史版本

处理询问时，只要找到对应版本，询问区间和即可

主席树：时间复杂度 $O(m \log n)$ ,空间复杂度 $O(m \log n)$

树套树：时间复杂度 $O(m \log m \log n)$ ,空间复杂度 $O(m \log n)$

期望得分：14分

结合其它算法可以得更高得分数

算法6

前面的树套树做法，如果能支持修改，就能AC

可以这样做：

维护动态开点树套树，线段树维护区间与 $h$ 取max/min标记

对于查询操作和模板基本一致，但遇到未建的节点需要特殊处理（当然也可以暴力建出来，不影响复杂度）

对于修改操作，先按普通线段树递归处理

递归到的节点，把它的平衡树削去一块，并把削去的一块拍扁，随后加上标记

在回去的时候，上面的节点也应删去对应内容

下放标记的时候，也是把平衡树削去一块，不过不用处理上边

复杂度可以这样考虑：

时间复杂度：

对于一个节点，它必须先被插入才能被删除，所以求出平衡树中节点总数即可

修改时，如果把平衡树上的节点都拆开，也就是，每次递归到一个完整区间，就会使其上面所有节点中加入一个点

这样节点总数是 $O(\log^2 n)$ 的，而pushdown最差情况下也不能增加节点数，只能把一堆节点的数改变

删除时最多删掉 $O(m\log ^2 n)$ 个节点

而实际上可以把相同数字的点合并，降低树高，使每次插入/删除操作复杂度为 $O(\log m)$

一次pushdown操作取决于平衡树的树高，而操作次数是 $O(m \log n)$ 的

所以时间复杂度就是 $O(m\log m\log^2n)$

但是可以进行优化，使得复杂度跑不满

空间复杂度：

考虑最多存在的节点数

在每一次操作中，涉及的线段树节点最多增加一种数，而每次涉及的线段树节点数是 $O(\log n)$ 的，pushdown不会增加涉及节点的数字种数，所以空间复杂度就是 $O(m\log n)$

（如果认为复杂度分析有问题，请私信作者）

时间复杂度 $O(m \log m \log^2n)$ ,空间复杂度 $O(m \log n)$

不过常数很大

期望得分：100分

实际得分取决于常数和空间使用情况，如果~~写得丑~~可能会卡常或者MLE

std最大的点用时2s多一点，空间约270MB

注：lxl说时间复杂度是两个log，然而我不会分析

i_m_a_ 2019-08-15 08:57
dalao能帮我分析一下我那道题中树套树的复杂度吗/kel

noip 毒瘤 2019-08-15 11:30
显然是nlog^2n吧，我记得是jry论文里面写过？

noip 毒瘤 2019-08-15 11:30
*集训队论文

算法7

针对#4

这个点 $n$ 很大，但是 $m$ 很小

考虑把一段区间压缩

对于操作，位于边界上的区间拆成两端，中间部分直接修改

对于询问，求出在区间内部分的长度，然后判断是否应该加到答案里

一个优化：每次操作后，将相邻且数字相同的区间合并

这样y优化后，是可以过纯随机数据的

但是，最后一行的字告诉我们，~~暴力不能出奇迹~~

时间复杂度 $O(m^2)$ ，空间复杂度 $O(m)$

期望得分：14分

算法8

考虑用优雅的暴力：块状链表

块状链表可以 $O(\sqrt n)$ 维护很多区间操作，而且支持插入

首先，每个块维护序列，以及序列被排序的结果

对于区间询问，边角自然是暴力，中间部分可以二分

对于区间操作，边角还是暴力，中间直接打标记

边角处理完后，需要重新排序

需要下放标记时，直接暴力把序列以及排序的结果修改即可

排序时，用基数排序，然后把块的大小设为 ${\sqrt{n}}{\log n}$ ，就可以做到 $O(n \sqrt{n \log n})$

时间复杂度 $O(n \sqrt{n} \log n)$ 或 $O(n \sqrt{n \log n})$ ，空间复杂度 $O(m)$

在题目的数据范围下时间复杂度与树套树接近，而且常数比树套树小，所以跑得比树套树快，std最慢的点不到1s，同时k空间复杂度小，也没有MLE的风险

~~所以事实是：暴力可以出奇迹~~

期望得分：100分

关于 $O(n \sqrt{n \log n})$ 分析：

按照上面的方式分块，可以发现：一共有 $O(\frac{\sqrt{n}}{\log n})$ 个块

每次操作最多暴力处理两个块，然后处理 $O(\frac{\sqrt{n}}{\log n})$ 个完整的块

对于暴力部分，询问、操作和下放标记都是单次 $O(1)$ 的，因而这部分时间复杂度是 $O(\frac{\sqrt{n}}{\log n})$ 的

对于整块，二分是单次 $O(\log n)$ ，打标记是 $O(1)$ ，乘以块的个数，就能得到这部分时间复杂度为 $O({\sqrt{n}}{\log n})$

上面的分析应该不完全正确，不过最多差一个 $O(\log \log n)$

其它

可能也有针对#7的离线做法，期望得分67分，不过我没想出来

~~也许复杂度分析错是树套树跑得比预想中慢的原因~~

~~lxl说可以卡块状链表，不过我感觉难度很大~~

代码

算法6和算法8都很难写，细节非常多

代码很长，而且很乱，基本没法看，不过还是发一下吧

~~由于出题人并不会写算法4的二维线段树，所以没有相应代码~~

算法6：

#include<cstdio>
#define gsz(x) (x?x->size:0)
const int Q=100007,logQ=20,logN=30;
const bool DEBUG=0;
const int INF=0x7fffffff;
bool f=0;
long long read(){
    long long n=0;char c=getchar();bool f=0;
    while(c!='-'&&(c<'0'||c>'9'))c=getchar();
    if(c=='-'){f=1;c=getchar();}
    while(c>='0'&&c<='9'){n=n*10+c-'0';c=getchar();}
    if(f)return -n;
    else return n;
}
char res[25];
void write(long long num){
    if(num==0){putchar('0');return;}
    if(num<0){putchar('-');num=-num;}
    int t=0;
    while(num){res[t++]=num%10+'0';num/=10;}
    while(t--)putchar(res[t]);
}
struct range{
	int num,len;
};
range list[Q*logQ*2];
int scnt;
int slen;
namespace FHQ{
	struct node{
		int num,cnt,rand,size;
		node *lcd,*rcd;
		void pushup(){
			size=gsz(lcd)+cnt+gsz(rcd);
			check();
		}
		void cseq(){
			if(lcd)lcd->cseq();
			list[scnt++]=(range){num,cnt};
			slen+=cnt;
			if(rcd)rcd->cseq();
		}
		void check(){
			if(this==lcd||this==rcd){
				throw 1;
			}
		}
	};
	namespace mem{
		int top;
		node mem[Q*logN*4];
		node *recy[Q*logN*4];
		int c;
		long long seed=84512021546LL;
		int rand(){
			return (int)(seed=seed*998244353+17);
		}
		node* get(int num,int cnt){
			if(cnt==0)return 0;
			node *cur;
			cur=mem+(++top);
			cur->num=num;
			cur->cnt=cnt;
			cur->size=cnt;
			cur->rand=rand();
			cur->lcd=cur->rcd=0;
			return cur;
		}
		void del(node *tr){
			if(!tr)return;
			if(tr->lcd)del(tr->lcd);
			if(tr->rcd)del(tr->rcd);
			recy[c++]=tr;
		}
	}
	void split_num(node *tr,int num,node * &l,node * &r){
		if(tr==0){l=r=0;return;}
		if(tr->num<num){
			split_num(tr->rcd,num,tr->rcd,r);
			l=tr;
			l->pushup();
		}else{
			split_num(tr->lcd,num,l,tr->lcd);
			r=tr;
			r->pushup();
		}
	}
	node *merge(node *l,node *r){
		if(l==0)return r;
		if(r==0)return l;
		if(l->rand>r->rand){
			l->rcd=merge(l->rcd,r);
			l->pushup();
			return l;
		}else{
			r->lcd=merge(l,r->lcd);
			r->pushup();
			return r;
		}
	}
	node *insert(node *tr,int num,int cnt){
		if(cnt==0)return tr;
		node *l,*m,*r;
		split_num(tr,num,l,r);
		split_num(r,num+1,m,r);
		if(m){m->cnt+=cnt;m->size+=cnt;}
		else m=mem::get(num,cnt);
		return merge(l,merge(m,r));
	}
	node *del(node *tr,int num,int cnt){
		if(cnt==0)return tr;
		node *l,*m,*r;
		split_num(tr,num,l,r);
		split_num(r,num+1,m,r);
		if(m->cnt==cnt){
			mem::del(m);
			return merge(l,r);
		}
		else{
			m->cnt-=cnt;
			m->size-=cnt;
			return merge(l,merge(m,r));
		}
	}
	int qrank(node *tr,int num){
		int ans=0;
		while(tr){
			if(tr->num<num){
				ans+=gsz(tr->lcd)+tr->cnt;
				tr=tr->rcd;
			}else{
				tr=tr->lcd;
			}
		}
		return ans;
	}
}

namespace seg{
	struct node{
		int tmax,tmin;
		node *lcd,*rcd;
		FHQ::node *tr;
		void pushdown(int ll,int rr);
		FHQ::node * smax(int num);
		FHQ::node * smin(int num);
		int qrank(int l,int r,int num,int ll,int rr){
			if(l<=ll&&rr<=r){
				if(tr){
					return FHQ::qrank(tr,num);
				}else{
					if(tmax<num)return rr-ll+1;
					else return 0;
				}
			}
			if(l>rr||ll>r)return 0;
			pushdown(ll,rr);
			int ans=0;
			int mid=((ll+rr)>>1);
			ans+=lcd->qrank(l,r,num,ll,mid);
			ans+=rcd->qrank(l,r,num,mid+1,rr);
			return ans;
		}
		void smax(int l,int r,int num,int ll,int rr){
			if(l<=ll&&rr<=r){
				if(tr){
					FHQ::node *t=smax(num);
					if(t){t->cseq();FHQ::mem::del(t);}
					
				}else{
					if(tmax>num){
						
						slen+=rr-ll+1;
						list[scnt++]=(range){tmin,rr-ll+1};
						tmax=tmin=num;
					}
				}
				return;
			}
			if(l>rr||ll>r)return;
			pushdown(ll,rr);
			int prcnt=scnt,prlen=slen;
			int mid=((ll+rr)>>1);
			lcd->smax(l,r,num,ll,mid);
			rcd->smax(l,r,num,mid+1,rr);
			for(;prcnt<scnt;prcnt++){
				tr=FHQ::del(tr,list[prcnt].num,list[prcnt].len);
			}
			tr=FHQ::insert(tr,num,slen-prlen);
		}
		void smin(int l,int r,int num,int ll,int rr){
			if(l<=ll&&rr<=r){
				if(tmin>=num)return;
				if(tr){
					FHQ::node *t=smin(num);
					if(t){t->cseq();FHQ::mem::del(t);}
				}else{
					slen+=rr-ll+1;
					list[scnt++]=(range){tmin,rr-ll+1};
					tmax=tmin=num;
				}
				return;
			}
			if(l>rr||ll>r)return;
			pushdown(ll,rr);
			int prcnt=scnt,prlen=slen;
			int mid=((ll+rr)>>1);
			lcd->smin(l,r,num,ll,mid);
			
			
			rcd->smin(l,r,num,mid+1,rr);
			
			
			
			
			for(;prcnt<scnt;prcnt++){
				tr=FHQ::del(tr,list[prcnt].num,list[prcnt].len);
			}
			tr=FHQ::insert(tr,num,slen-prlen);
		}
	};
	namespace mem{
		int top;
		node mem[Q*logN*3];
		int c;
		node *recy[Q*logN*3];
		node *get(int num){
			node *cur;
			if(c)cur=recy[--c];
			else cur=mem+(++top);
			cur->tmax=cur->tmin=num;
			cur->tr=0;
			cur->lcd=cur->rcd=0;
			return cur;
		}
		void del(node *tr){
			if(tr->lcd)del(tr->lcd);
			if(tr->rcd)del(tr->rcd);
			if(tr->tr)FHQ::mem::del(tr->tr);
			recy[c++]=tr;
		}
	}
	FHQ::node * node::smin(int num){
		if(tmin>=num)return 0;
		tmin=num;
		if(num>=tmax){
			FHQ::node *r=tr;
			tmax=tmin=num;
			FHQ::mem::del(tr);
			tr=0;
			if(lcd)mem::del(lcd);
			if(rcd)mem::del(rcd);
			lcd=rcd=0;
			return r;
		}
		FHQ::node *l,*r;
		FHQ::split_num(tr,num+1,l,r);
		tr=FHQ::merge(FHQ::mem::get(num,gsz(l)),r);
		return l;
	}
	FHQ::node * node::smax(int num){
		if(tmax<=num)return 0;
		tmax=num;
		if(num<=tmin){
			FHQ::node *r=tr;
			tmax=tmin=num;
			FHQ::mem::del(tr);
			tr=0;
			if(lcd)mem::del(lcd);
			if(rcd)mem::del(rcd);
			lcd=rcd=0;
			return r;
		}
		FHQ::node *l,*r;
		FHQ::split_num(tr,num,l,r);
		tr=FHQ::merge(l,FHQ::mem::get(num,gsz(r)));
		return r;
	}
	void node::pushdown(int ll,int rr){
		if(ll==16&&rr==20){
			ll++;
			ll--;
		}
		if(!tr){
			lcd=mem::get(tmax);
			rcd=mem::get(tmax);
			tr=FHQ::mem::get(tmax,rr-ll+1);
			tmax=INF;
			tmin=0;
			return;
		}
		if(tmax!=INF){
			lcd->smax(tmax);
			rcd->smax(tmax);
			tmax=INF;
		}
		if(tmin!=0){
			lcd->smin(tmin);
			rcd->smin(tmin);
			tmin=0;
		}
	}
}
seg::node *root;
int lastans,k,opt,l,r,num,n,m,v;
int main(){
	n=read();m=read();k=read();
	root=seg::mem::get(0);
	for(int t=1;t<=m;t++){
		if(t==43){
			t=t+1;
			t--;
		}
		scnt=slen=0;
		opt=read();
		switch(opt){
			case 1:
				l=(read()^lastans*k);
				r=(read()^lastans*k);
				num=(read()^lastans*k);
				lastans=root->qrank(l,r,num,1,n);
				write(lastans);putchar('\n');
				
				break;
			case 2:
				l=(read()^lastans*k);
				r=(read()^lastans*k);
				num=(read()^lastans*k);
				root->smax(l,r,num,1,n);
				
				break;
			case 3:
				l=(read()^lastans*k);
				r=(read()^lastans*k);
				num=(read()^lastans*k);
				root->smin(l,r,num,1,n);
				
				break;
			case 4:
				return 1;
				break;
		}
	}
}

算法8：

#include<cstdio>
#include<cmath>
#include<algorithm>
const int N=1000007,sqrtN=2000;
bool f=0;
long long read(){
    long long n=0;char c=getchar();bool f=0;
    while(c!='-'&&(c<'0'||c>'9'))c=getchar();
    if(c=='-'){f=1;c=getchar();}
    while(c>='0'&&c<='9'){n=n*10+c-'0';c=getchar();}
    if(f)return -n;
    else return n;
}
char res[25];
void write(long long num){
    if(num==0){putchar('0');return;}
    if(num<0){putchar('-');num=-num;}
    int t=0;
    while(num){res[t++]=num%10+'0';num/=10;}
    while(t--)putchar(res[t]);
}
struct range{
    int len,num;
    void put(){
        for(int i=0;i<len;i++){
            write(num);
            putchar(' ');
        }
    }
};
int cntl[256];
range swp[sqrtN*4];int cnt;
void sort(range *st,range *en){
	int n=en-st;
	range *list=st;
	
	for(int i=0;i<256;i++)cntl[i]=0;
	for(int i=0;i<n;i++)cntl[list[i].num&0xff]++;
	for(int i=1;i<256;i++)cntl[i]+=cntl[i-1];
	for(int i=n-1;i>=0;i--)swp[--cntl[list[i].num&0xff]]=list[i];
	
	for(int i=0;i<256;i++)cntl[i]=0;
	for(int i=0;i<n;i++)cntl[(swp[i].num>>8)&0xff]++;
	for(int i=1;i<256;i++)cntl[i]+=cntl[i-1];
	for(int i=n-1;i>=0;i--)list[--cntl[(swp[i].num>>8)&0xff]]=swp[i];
	
	for(int i=0;i<256;i++)cntl[i]=0;
	for(int i=0;i<n;i++)cntl[(list[i].num>>16)&0xff]++;
	for(int i=1;i<256;i++)cntl[i]+=cntl[i-1];
	for(int i=n-1;i>=0;i--)swp[--cntl[(list[i].num>>16)&0xff]]=list[i];
	
	for(int i=0;i<256;i++)cntl[i]=0;
	for(int i=0;i<n;i++)cntl[(swp[i].num>>24)&0xff]++;
	for(int i=1;i<256;i++)cntl[i]+=cntl[i-1];
	for(int i=n-1;i>=0;i--)list[--cntl[(swp[i].num>>24)&0xff]]=swp[i];
}
bool cmp(range a,range b){
    return a.num<b.num;
}

struct block;
int deflen;
int slen; 
struct block{
    block* nxt;
    int len;
    int size;
    int tmax,tmin;
    range list[sqrtN*2],sorted[sqrtN*2];
    
    int sum[sqrtN*2];
    
    void build(){
        size=0;
        tmax=0x7fffffff;
        tmin=0;
        for(int i=0;i<len;i++){
            sorted[i]=list[i];
        }
        sort(sorted,sorted+len);
        sum[0]=0;
        for(int i=1;i<=len;i++){
            sum[i]=sum[i-1]+sorted[i-1].len;
        }
        size=sum[len];
    }
    void pushdown(){
        int i=0;
        for(;i<len;i++){
            if(list[i].num<tmin)list[i].num=tmin;
            if(list[i].num>tmax)list[i].num=tmax;
        }
        i=0;
        for(;i<len;i++){
            if(sorted[i].num<tmin)sorted[i].num=tmin;
            if(sorted[i].num>tmax)sorted[i].num=tmax;
        }
        tmax=0x7fffffff;
        tmin=0;
    }
    void rebuild();
    int qrank(int num){
        if(num>tmax)return size;
        if(num<=tmin)return 0;
        int l=0,r=len,mid;
        while(l!=r){
            mid=((l+r)>>1);
            if(sorted[mid].num<num)l=mid+1;
            else r=mid;
        }
        return sum[l];
    }
    int qrank(int l,int r,int num){
        pushdown();
        if(num>tmax)return r-l+1;
        if(num<=tmin)return 0;
        if(l<0)l=0;
        if(r>=size)r=size-1;
        int ans=0,pre=0,i;
        for(i=0;;i++){
            if(pre+list[i].len-1>=l)break;
            pre+=list[i].len;
        }
        if(pre+list[i].len-1>=r){
            if(list[i].num<num)ans=r-l+1;
            else ans=0;
        }else{
            if(list[i].num<num)ans+=(pre+list[i].len)-l;
            pre+=list[i].len;
            i++;
            for(;;i++){
                if(pre+list[i].len-1>=r)break;
                if(list[i].num<num)ans+=list[i].len;
                pre+=list[i].len;
            }
            if(list[i].num<num)ans+=r-pre+1;
        }
        return ans;
    }
    void smax(int num){
        if(num<tmax){
            tmax=num;
            if(num<tmin){
                tmin=num;
            }
        }
    }
    bool smax(int l,int r,int num){
        slen-=len;
        pushdown();
        if(l<0)l=0;
        if(r>=size)r=size-1;
        int i=0,pre=0,j=0;
        for(;;i++){
            if(list[i].len==0)continue;
            if(pre+list[i].len-1>=l)break;
            swp[j++]=list[i];
            pre+=list[i].len;
        }
        if(pre+list[i].len-1>=r){
            if(list[i].num>num){
                int ll=pre,rr=pre+list[i].len-1;
                if(ll!=l)swp[j++]=(range){l-ll,list[i].num};
                swp[j++]=(range){r-l+1,num};
                if(rr!=r)swp[j++]=(range){rr-r,list[i].num};
                pre+=list[i].len;
                i++;
            }else{
                pre+=list[i].len;
                swp[j++]=list[i++];
            }
        }else{
            if(list[i].num>num){
                int ll=pre,rr=pre+list[i].len-1;
                if(ll!=l)swp[j++]=(range){l-ll,list[i].num};
                swp[j++]=(range){rr-l+1,num};
                pre+=list[i].len;
                i++;
            }else{
                pre+=list[i].len;
                swp[j++]=list[i++];
            }
            for(;;i++){
                if(list[i].len==0)continue;
                if(pre+list[i].len-1>=r)break;
                if(list[i].num>num){
                    swp[j++]=(range){list[i].len,num};
                }else{
                    swp[j++]=list[i];
                }
                pre+=list[i].len;
            }
            if(list[i].num>num){
                int ll=pre,rr=pre+list[i].len-1;
                swp[j++]=(range){r-ll+1,num};
                if(ll!=l)swp[j++]=(range){rr-r,list[i].num};
                pre+=list[i].len;
                i++;
            }else{
                pre+=list[i].len;
                swp[j++]=list[i++];
            }
        }
        for(;i<len;i++){
            if(list[i].len==0)continue;
            swp[j++]=list[i];
            pre+=list[i].len;
        }
        
        cnt=j;
        if(j!=1&&j>=deflen){
            rebuild();
            slen+=len;
            return 1;
        }else{
            len=j;
            for(i=0;i<j;i++){
                list[i]=swp[i];
            }
            build();
            slen+=len;
            return 0;
        }
        
    }
    void smin(int num){
        if(num>tmin){
            tmin=num;
            if(num>tmax){
                tmax=num;
            }
        }
    }
    bool smin(int l,int r,int num){
        slen-=len;
        pushdown();
        if(l<0)l=0;
        if(r>=size)r=size-1;
        int i=0,pre=0,j=0;
        for(;;i++){
            if(list[i].len==0)continue;
            if(pre+list[i].len-1>=l)break;
            swp[j++]=list[i];
            pre+=list[i].len;
        }
        if(pre+list[i].len-1>=r){
            if(list[i].num<num){
                int ll=pre,rr=pre+list[i].len-1;
                if(ll!=l)swp[j++]=(range){l-ll,list[i].num};
                swp[j++]=(range){r-l+1,num};
                if(rr!=r)swp[j++]=(range){rr-r,list[i].num};
                pre+=list[i].len;
                i++;
            }else{
                swp[j++]=list[i++];
            }
        }else{
            if(list[i].num<num){
                int ll=pre,rr=pre+list[i].len-1;
                if(ll!=l)swp[j++]=(range){l-ll,list[i].num};
                swp[j++]=(range){rr-l+1,num};
                pre+=list[i].len;
                i++;
            }else{
                pre+=list[i].len;
                swp[j++]=list[i++];
            }
            for(;;i++){
                if(list[i].len==0)continue;
                if(pre+list[i].len-1>=r)break;
                if(list[i].num<num){
                    swp[j++]=(range){list[i].len,num};
                }else{
                    swp[j++]=list[i];
                }
                pre+=list[i].len;
            }
            if(list[i].num<num){
                int ll=pre,rr=pre+list[i].len-1;
                swp[j++]=(range){r-ll+1,num};
                if(ll!=l)swp[j++]=(range){rr-r,list[i].num};
                pre+=list[i].len;
                i++;
            }else{
                swp[j++]=list[i++];
            }
        }
        for(;i<len;i++){
            if(list[i].len==0)continue;
            swp[j++]=list[i];
            pre+=list[i].len;
        }
        
        cnt=j;
        if(j!=1&&j>=deflen){
            rebuild();
            slen+=len;
            return 1;
        }else{
            len=j;
            for(i=0;i<j;i++){
                list[i]=swp[i];
            }
            build();
            slen+=len;
            return 0;
        }
    }
    void clr(int num,int _len){
        slen-=len;
        list[0]=(range){_len,num};
        sorted[0]=(range){_len,num};
        sum[0]=0;
        sum[1]=_len;
        len=1;
        size=_len;
        tmax=0x7fffffff;
        tmin=0;
        slen+=len;
    }
    void chklen(int pre,int sum){
        for(int i=0;i<len;i++){
            pre+=list[i].len;
        }
        if(nxt)nxt->chklen(pre,sum);
        else{
            if(pre!=sum){
                throw 1;
            }
        }
    } 
};
namespace mem{
    block mem[sqrtN*3];
    int top;
    block* recy[sqrtN*3];
    int rc;
    block* get(){
        if(rc){
            return recy[--rc];
        }else{
            return mem+(top++);
        }
    }
    void del(block* t){
        recy[rc++]=t;
    }
    
}
void block::rebuild(){
    if(cnt==1)return;
    block* nx1=mem::get();
    int m=(cnt>>1);
    for(int i=0;i<m;i++)list[i]=swp[i];
    for(int i=m,j=0;i<cnt;i++,j++)nx1->list[j]=swp[i];
    nx1->len=cnt-m;
    len=m;
    build();
    nx1->build();
    nx1->nxt=nxt;
    nxt=nx1;
    if((sum[1]!=sorted[0].len)||(nxt->sum[1]!=nxt->sorted[0].len)){
    	throw 1;
    }
}
block *st;
bool jmp;
int lastans,k,opt,l,r,num,n,m,v;
int main(){
    n=read();m=read();k=read();
    
    deflen=sqrt(m*log(m+4)/35/log(2))+1;
    slen=1;
    
    st=mem::get();
    st->list[0]=(range){n,0};
    st->len=1;
    st->build();
    
    for(int t=1;t<=m;t++){
        opt=read();
        block *cur=st;
        int pre=0;
        switch(opt){
            case 1:
                l=(read()^lastans*k)-1;
                r=(read()^lastans*k)-1;
                num=(read()^lastans*k);
                lastans=0;
                while(1){
                    if(pre+cur->size-1>=l)break;
                    pre+=cur->size;
                    cur=cur->nxt;
                }
                if(pre+cur->size-1>=r){
                    lastans=cur->qrank(l-pre,r-pre,num);
                }else{
                    lastans+=cur->qrank(l-pre,cur->size-1,num);
                    pre+=cur->size;
                    cur=cur->nxt;
                    while(1){
                        if(pre+cur->size-1>=r)break;
                        lastans+=cur->qrank(num);
                        pre+=cur->size;
                        cur=cur->nxt;
                    }
                    lastans+=cur->qrank(0,r-pre,num);
                }
                write(lastans);putchar('\n');
                
                break;
            case 2:
                l=(read()^lastans*k)-1;
                r=(read()^lastans*k)-1;
                num=(read()^lastans*k);
                
                while(1){
                    if(pre+cur->size-1>=l)break;
                    pre+=cur->size;
                    cur=cur->nxt;
                }
                if(pre+cur->size-1>=r){
                    jmp=cur->smax(l-pre,r-pre,num);
                    if(jmp){pre+=cur->size;cur=cur->nxt;}
                }else{
                    jmp=cur->smax(l-pre,cur->size-1,num);
                    if(jmp){pre+=cur->size;cur=cur->nxt;}
                    pre+=cur->size;
                    cur=cur->nxt;
                    
                    while(1){
                        if(pre+cur->size-1>=r)break;
                        cur->smax(num);
                        pre+=cur->size;
                        cur=cur->nxt;
                    }
                    cur->smax(0,r-pre,num);
                }
                
                break;
            case 3:
                l=(read()^lastans*k)-1;
                r=(read()^lastans*k)-1;
                num=(read()^lastans*k);
                
                while(1){
                    if(pre+cur->size-1>=l)break;
                    pre+=cur->size;
                    cur=cur->nxt;
                }
                if(pre+cur->size-1>=r){
                    jmp=cur->smin(l-pre,r-pre,num);
                    if(jmp){pre+=cur->size;cur=cur->nxt;}
                }else{
                    jmp=cur->smin(l-pre,cur->size-1,num);
                    if(jmp){pre+=cur->size;cur=cur->nxt;}
                    pre+=cur->size;
                    cur=cur->nxt;
                    
                    while(1){
                        if(pre+cur->size-1>=r)break;
                        cur->smin(num);
                        pre+=cur->size;
                        cur=cur->nxt;
                    }
                    cur->smin(0,r-pre,num);
                }
                
                break;
            case 4:
                return 1;
                break;
        }
        f=0;
    }
}

~~代码长度堪比猪国杀~~

ID

4471

时间

3000ms

内存

500MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

算法1

算法2

算法3

算法4

算法5

算法6

算法7

算法8

关于 $O(n \sqrt{n \log n})$ 分析：

其它

代码

决战

信息

1 条题解

自动搬运

以下是正文

算法1

算法2

算法3

算法4

算法5

算法6

算法7

算法8

关于O(nnlog⁡n)O(n \sqrt{n \log n})O(nnlogn​)分析：

其它

代码

决战

信息

还没有账户？

登录

关于 $O(n \sqrt{n \log n})$ 分析：