自动搬运

查看原文

来自洛谷，原作者为

	功在不舍 骐骥一跃，不能十步；驽马十驾，功在不舍。锲而舍之，朽木不折；锲而不舍，金石可镂。

搬运于2025-08-24 22:11:22，当前版本为作者最后更新于2020-04-28 18:36:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

感觉题解们都不太对我这种萌新友好啊

我来一篇带图的题解把。

1.引入：我们来考虑一个问题，怎么求一个串有多少个本质不同的子串？

如果你用暴力枚举子串或者$Manacher+hash$，都是$O(n^2)$的太慢了。

他们没有利用到各个回文子串之间的包含关系，所以比较慢。 zzh 回文自动机就是来利用这种关系解决问题$O(n)$算法

2.回文树

和AC自动机一样，回文自动机也要有一颗树把回文串“串起来”。

我们知道一个长的回文串去掉他的两头，能得到一个短回文串，

我们利用回文字符串这样性质把他们折叠挂在树上。

但是长度为奇数的回文子串 有中心，而长度为 偶数的回文子串没有。

我们要把长度为奇数、偶数的分开挂着。

0代表偶数长度的根，1代表奇数长度的根。

树上的每一个点都代表一个不同的回文子串（不含0，1）

以abbaabba为例子，下面是他的回文树，上面串着所有他的回文串。

挂的同时我们还可以统计各个回文子串的长度。

$len[0]=0,len[1]=-1$

其他的点深度+1，len就比父节点增加2。

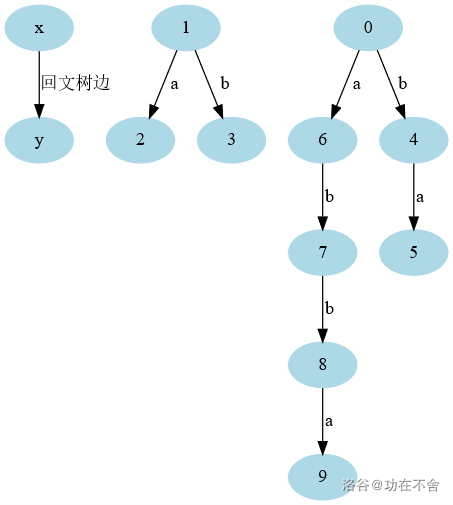
注意这里节点代表的状态和 $trie$ 树不一样。

状态应该从下往上再往下读。

例如8号点代表的回文子串是 $bbaabb$

注意如果在奇数树上，最顶上的边只能读1次。

这棵树的节点个数-2就是abbaabba本质不同的回文串个数。

3.$O(n)$构建与$fail$

我们肯定不能直接暴力把所有回文子串挂上去。

我们用一种类似后缀树的办法 “增量构造”

即利用$s[0\ to\ i-1]$的回文树，加入$s[i]$位得到新的回文树。

明显，我们可能会得到一些新的回文子串，考虑怎么把他放到树上。

由于所有新产生的回文子串都是新最长回文子串的回文后缀，且长度应比最长的小，我们可以把他们“翻转”一下，就可以发现他们一定在$s[0\ to \ i-1]$的回文树里！（即同时也是前缀）

所以插入一个新点，最多只会建立“最长新回文后缀”这么一个节点，保证了回文自动机的点数是$O(n)$的。

这也告诉我们一个串的本质不同的回文子串最多有n个，由$aaaa.....$取到，于是问题转化为了怎么把这一个回文串放到树上。

首先，我们可以发现，如果设新产生的回文子串中长度最大的长度为$len$,则$s[i-len+2\ \ to\ \ i-1]$（就是掐头去尾）一定也是一个回文串（$len=0$直接不用管了）。

其次，这个回文串一定是$s[0\ to\ i-1]$满足$s[i-len[x]-1]=s[i]$的最长回文后缀 $x$，否则添头增尾得到的新的回文子串不是最长的。

“最长”“后缀”让我们想到了什么？$->AC:fail[x]$

类似的，定义fail[x]为x代表的回文子串的最长回文后缀。

假设 以$i-1$位结束的最长回文子串在$cur$位置

$cur,fail[cur],fail[fail[cur]] ......$一定包含了所有新产生的回文子串。（其中合法的是满足$s[i-len[x]-1]==s[i]$的）

$while$遍历，当其中第一次遇到$s[i-len[x]-1]==s[i]$时，一定是新的最长回文后缀,如果那一位在回文数上有$s[i]$这个子节点就直接走过去(重复了)，否则就新建一个。（是不是和AC自动机很像）

下图是abbaabba的完整回文自动机。

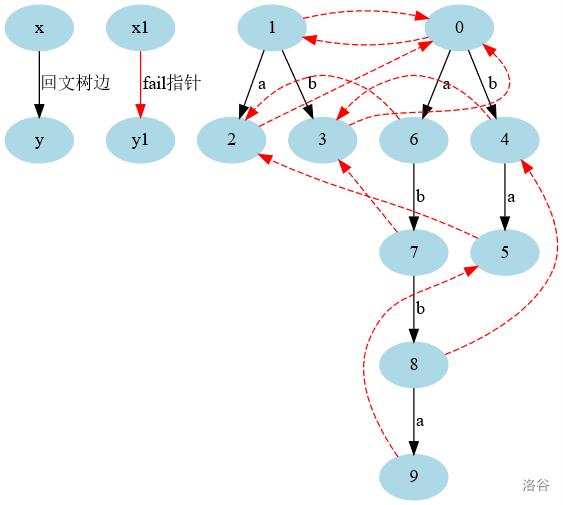
你可能会疑惑，0、1一个是偶数空，一个是奇数空，他们的$fail$是干嘛的？

考虑$abbac$,加入到$c$的时候，不管你怎么跳$fail$都匹配不上，但是它 会在奇数根1下面挂上，表示单独的字符C。

$fail[0]=1$ 结合上面的图你可以发现，当出现我说的情况时，fail最后会从奇数根下面的某一位 跳到0，若0也不能增加，就得跳到1去了(奇数根一定可以挂，想想为什么)，让0指向1，就实现了增添新的单独字符的功能。

你可能又会问了，这样不是跳了两次吗，为什么不让奇数根下面的字符直接$fail=1$,而是让他等于0？

这当然是不对的，跳$fail$的本质过程是判断能不能加入新的位，不能在单个字符周围加入新的字符形成长度为3的新回文串，不代表不能再“0空”位置形成 $aa,bb,cc$这样长度为2的回文串。

本模板题要求以每一位结尾的回文子串个数，设$num[x]$为回文自动机上$x$号点中回文子串个数，当新加入一个点$tot$时，$num[tot]=num[fail[tot]]+1$，即比他的最长回文后缀多含有一个回文子串。

以下是代码,说几个细节问题。

1.如果$i$从$0$开始，$i-len[x]-1$可能出现负数，特判一下。

2.求新点的$fail$时是$getfail(fail[pos],i)$，如果写成了$getfail(pos,i)$，自己会被当成是自己的最长回文后缀(和AC自动机一样不允许！)，$fail$指向自己会导致程序死循环。

3.求新点的$fail$必须在建立新点之前！

否则考虑 要建立奇数根下的点时（abbbc），他们$fail[i]=0$,$getfail(fail[pos],i)$会跳到1(0匹配的话不会再1下建点)，如果1下已经建立它的点，$fail$也会指向他自己导致程序卡死！

时间复杂度$O(n)$，首先建立的节点数是$O(n)$的，其次因为每次执行$while$循环的时候cur的深度会-1，而cur的深度总共增加了n次（for循环中），所以$while$的执行次数也是$O(n)$的

差不多了完结撒花~

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char s[2000001];
int len[2000001],n,num[2000001],fail[2000001],last,cur,pos,trie[2000001][26],tot=1;
int getfail(int x,int i)
{
	while(i-len[x]-1<0||s[i-len[x]-1]!=s[i])x=fail[x];
	return x;
}
int main()
{
	scanf("%s",s);
    n=strlen(s);
    fail[0]=1;len[1]=-1;
    for(int i=0;i<=n-1;i++){
    	if(i>=1)s[i]=(s[i]+last-97)%26+97; 
    	pos=getfail(cur,i);
        //找到cur的fail链中能匹配i位的最长回文后缀
        if(!trie[pos][s[i]-'a']){
        	fail[++tot]=trie[getfail(fail[pos],i)][s[i]-'a'];
        	trie[pos][s[i]-'a']=tot;
        	len[tot]=len[pos]+2;
            num[tot]=num[fail[tot]]+1;
		}//不存在建立点，存在直接走过去
        cur=trie[pos][s[i]-'a'];
        last=num[cur];
		printf("%d ",last);	   
	}
	return 0;
}