自动搬运

查看原文

来自洛谷，原作者为

	ix35 垒球

搬运于2025-08-24 22:11:20，当前版本为作者最后更新于2020-01-26 15:56:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

线段树合并&分裂

网上找线段树合并/分裂的博客，讲得很清楚的也不多，某些部分只有自己 yy 一下了。

前置芝士：权值线段树，动态开点线段树。

在以下讨论中，我们设值域都为 $[1,n]$ 中的整数。

先定义代码中的一些东西：

$ch[i][0]$ 表示 $i$ 的左子结点，$ch[i][1]$ 表示 $i$ 的右子结点，$val[i]$ 表示 $i$ 点维护的值（出现了多少个该值域中的数）

---

一、线段树合并

有时我们需要整合两棵权值线段树的信息，这个整合的过程称为线段树合并。我们以最简单的合并为例：将两棵树相加。

两棵树如何相加呢？在权值线段树上，每个点维护了一个当前区间中数的个数，而数的个数是可以相加的，这个合并的过程可以理解为：把两个可重集合并，对应的权值线段树上发生的过程。而相加的原理很简单，两棵同构的线段树，只需要对应位置相加即可，如图：

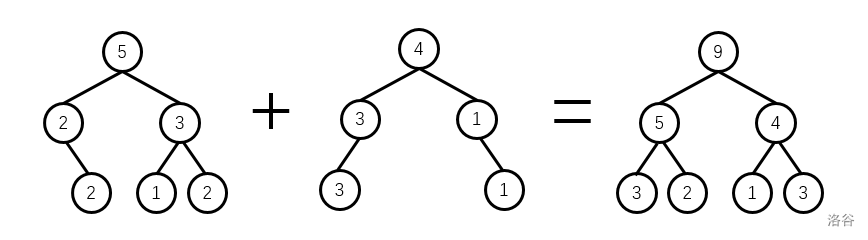
注意动态开点线段树上某些点是缺的，其值当然是 $0$。

如何合并两棵线段树呢？

暴力是很简单的，我们枚举 $1$ 到 $n$，将第二棵树中对应位置上的值在第一棵树上做单点修改即可。

这个方法可以用启发式合并进一步优化，但只能适用于一些特殊情况（比如说如果带了分裂或者一个值在多棵树上出现，启发式合并就歇菜了）。

---

而我们可以递归处理线段树合并，设我们现在要合并的是以 $x,y$ 为根的两棵子树，要确保它们在线段树上处于同一位置（即它们是两棵树上代表同一区间的点）。

如果 $x,y$ 其中一个为 $0$ （也就是某个权值线段树上没有这个位置的点），无需合并，返回另一个非 $0$ 的点即可。

否则，我们先合并 $x,y$ 的左右子结点，再根据两子结点的信息整合得到 $x,y$ 合并的结果。

线段树合并一般有两种写法：新建结点和不新建结点。但是两者原理是一样的。

新建结点的写法：

新建一个结点 $p$ 作为 $x,y$ 合并的结果。将 $ch[x][0]$ 和 $ch[y][0]$ 的合并结果记为 $sl$，$ch[x][1]$ 和 $ch[y][1]$ 的合并结果记为 $sr$，令 $sl,sr$ 分别为 $p$ 的两个子结点，对 $p$ 做一次 pushup​ 即可得到结果。此后 $x,y$ 就没有用的，可以回收（节省空间的方法）。但是有时 $x,y$ 的信息不能丢，这时就不能回收。

（这里原先的代码有点问题，先删了）

不新建结点的写法：

如果一个点合并完就可以扔掉，那还可以写得更加简便，直接将 $x$ 作为合并后的结果，将 $y$ 的值加到 $x$ 上即可（直接对应位置相加），甚至不需要 pushup，但是注意，如果 $x=0$，返回的是 $y$，所以比较保险的写法是 $x=merge(x,y)$。

事实上这里我们连当前区间的左右端点 $l,r$ 也可以去掉，因为到叶结点后 $ch[x][i]$ 自然是 $0$，自然会返回。

int merge (int x,int y) {
   	if (!x||!y) {return x+y;}     // 只有一边有点，不用合并
   	val[x]+=val[y];               // 信息整合
   	ch[x][0]=merge(ch[x][0],ch[y][0]);
   	ch[x][1]=merge(ch[x][1],ch[y][1]);
   	del(y);                       // 垃圾回收
   	return x;
}

这东西看着很一般，复杂度怎么样呢？

单独讨论一次合并的复杂度没有什么意义，如果两棵树都是满的，复杂度就到 $O(n)$ 了，所以一般从均摊角度来讨论。

---

如果现在有 $m$ 棵线段树（每棵树初始只有一个位置有权值），经过若干次合并最后变成 $1$ 棵，此过程的复杂度是多少呢？

例题：P4556，P5298

不说具体怎么做了，这些题都有很完整的题解，我就分析一下复杂度（这些题都符合上面提到的模型）。

一开始有 $m$ 棵树，只有一个位置有权值，所以一棵树上结点数量为 $O(\log n)$，$m$ 棵树的结点总数也就是 $O(m\log n)$。

分析上面的代码，发现每一次进入 merge 函数，要么停止递归，要么继续递归并有一个点被垃圾回收。显然停止递归的 merge 次数与继续递归的 merge 次数同阶（不继续递归的情况是从递归的情况出来的，不会超过其两倍的数量）。

因此整个过程的复杂度就等于继续递归的 merge 函数进入次数的复杂度（每一次执行 merge 在不考虑递归时复杂度 $O(1)$），也就等同于被删除的结点个数，是不超过 $O(m\log n)$ 的（有点像势能分析？）。

注意复杂度本身和是否回收结点没有关系，只是借以分析而已。

所以整个过程的复杂度也就是 $O(m\log n)$。

但是线段树合并的复杂度不总是对的，不过本题中 $1$ 操作的复杂度我不知道是否是均摊 $\log n$ 的，希望有人能证明/证伪一下。

---

二、线段树分裂

将一个可重集前 $k$ 小的数与之后的数分成两个集合，那么对应的权值线段树就要裂成两棵权值线段树。

举个栗子：将 $[1,3]$ 和 $[4,4]$ 分开（这里为了方便直接用权值描述了，一般是按照第 $k$ 小的位置来的）：

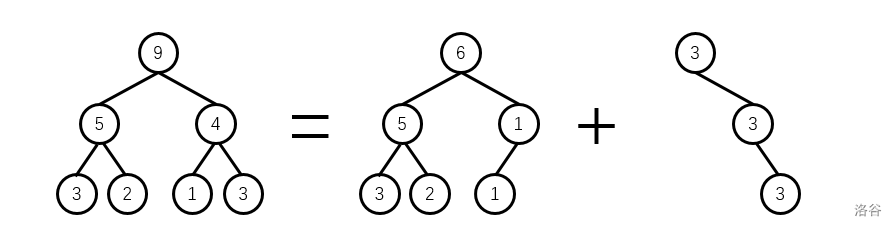
暴力当然也很简单，找到第 $k$，后面的值新建一棵树，在原树上减掉即可。

然而我们可以仿照 FHQ Treap 的套路，实现 $O(\log n)$ 的分裂。

设我们现在要将以 $x$ 为根的树分裂成 $x,y$ 为根的这两棵树（$y$ 本来是不存在的，传引用），以第 $k$ 小为界，前 $k$ 小在 $x$，之后的在 $y$。

首先看 $x$ 的左子树的值 $v$，如果 $v<k$，那么左侧依然归 $x$（不需要处理），递归右侧即可，注意 $k$ 变成了 $k-v$。

如果 $v=k$，那么左边归 $x$，右边归 $y$ 即可。

如果 $v>k$，那么右边归 $y$，递归左侧即可。

看完结构后看权值，$x$ 的新权值当然是 $k$，那么 $y$ 的权值也就是 $x$ 原先的权值减去 $k$ 了。

可以发现，如果 $v\ge k$，那么 $y$ 的右子结点都是需要赋值的，下面的代码直接归到了同一句里（else 所在的那一句）：

void split (int x,int &y,ll k) {
	y=newnod();
	ll v=val[ch[x][0]];
	if (k>v) {split(ch[x][1],ch[y][1],k-v);}
	else {swap(ch[x][1],ch[y][1]);}         // 右子树归 y，x 的右子树变成 0
	if (k<v) {split(ch[x][0],ch[y][0],k);}
	val[y]=val[x]-k;
	val[x]=k;
	return;
}

这个每次只递归一边，复杂度是 $O(\log n)$ 没啥问题。

---

三、这道题

每个操作分别来看。

将 $[x,y]$ 分裂出来：先分出 $[1,x-1]$，再从 $[x,n]$ 中分出 $[x,y]$ 和 $[y+1,n]$，最后把 $[1,x-1]$ 和 $[y+1,n]$ 合并。我注意到 std 不是这样的，std 的分裂写的就是分裂出一个区间，我在这里用了一次合并，但是复杂度是对的，稍后会证明复杂度为 $O(\log n)$；

将 $t$ 树合并入 $p$ 树：单次合并即可，不确定复杂度，但是不超过 $2\times 10^3$ 次总没问题的；

$p$ 树中插入 $a$ 个 $q$：单点修改，复杂度 $O(\log n)$；

查询 $[x,y]$ 中数的个数：区间求和，复杂度 $O(\log n)$；

查询第 $k$ 小：经典操作，复杂度 $O(\log n)$。

最后说一下 $0$ 操作的复杂度：

两次分裂是 $O(\log n)$ 没问题，主要看合并。注意合并的两个区间没有交集，我们就看一看每一层会涉及几个点。

对于第 $1$ 层：总共就 $1$ 个点...

对于第 $i$ 层：如果第 $i-1$ 层只递归下来 $1$ 个点（设为 $u$），再设 $x$ 和 $y$ 为 $u$ 的左右子结点。如果前一棵树占了 $x,y$ 两个点，那么因为后一棵树占的区间严格在前一棵树之后，所以只会占 $y$，那么需要递归的只有 $y$，反过来的话同理需要递归的只有 $x$，所以第 $i$ 层也只需要递归 $1$ 个点。

每一层只往下递归一个点，复杂度就是 $O(\log n)$ 了。

代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN=200010;
int n,m,tot,cnt,seq=1,op,x,y,z,bac[MAXN<<5],ch[MAXN<<5][2],rt[MAXN];
ll val[MAXN<<5];
int newnod () {return (cnt?bac[cnt--]:++tot);}
void del (int p) {
	bac[++cnt]=p,ch[p][0]=ch[p][1]=val[p]=0;
	return;
}
void modify (int &p,int l,int r,int pos,int v) {
	if (!p) {p=newnod();}
	val[p]+=v;
	if (l==r) {return;}
	int mid=(l+r)>>1;
	if (pos<=mid) {modify(ch[p][0],l,mid,pos,v);}
	else {modify(ch[p][1],mid+1,r,pos,v);}
	return;
}
ll query (int p,int l,int r,int xl,int xr) {
	if (xr<l||r<xl) {return 0;}
	if (xl<=l&&r<=xr) {return val[p];}
	int mid=(l+r)>>1;
	return query(ch[p][0],l,mid,xl,xr)+query(ch[p][1],mid+1,r,xl,xr);
}
int kth (int p,int l,int r,int k) {
	if (l==r) {return l;}
	int mid=(l+r)>>1;
	if (val[ch[p][0]]>=k) {return kth(ch[p][0],l,mid,k);}
	else {return kth(ch[p][1],mid+1,r,k-val[ch[p][0]]);}
}
int merge (int x,int y) {
	if (!x||!y) {return x+y;}
	val[x]+=val[y];
	ch[x][0]=merge(ch[x][0],ch[y][0]);
	ch[x][1]=merge(ch[x][1],ch[y][1]);
	del(y); 
	return x;
}
void split (int x,int &y,ll k) {
	if (x==0) {return;}
	y=newnod();
	ll v=val[ch[x][0]];
	if (k>v) {split(ch[x][1],ch[y][1],k-v);}
	else {swap(ch[x][1],ch[y][1]);}
	if (k<v) {split(ch[x][0],ch[y][0],k);}
	val[y]=val[x]-k;
	val[x]=k;
	return;
}
int main () {
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++) {
		scanf("%d",&x);
		modify(rt[1],1,n,i,x);
	}
	for (int i=1;i<=m;i++) {
		scanf("%d",&op);
		if (op==0) {
			scanf("%d%d%d",&x,&y,&z);
			ll k1=query(rt[x],1,n,1,z),k2=query(rt[x],1,n,y,z);
			int tmp=0;
			split(rt[x],rt[++seq],k1-k2);
			split(rt[seq],tmp,k2);
			rt[x]=merge(rt[x],tmp);
		} else if (op==1) {
			scanf("%d%d",&x,&y);
			rt[x]=merge(rt[x],rt[y]);
		} else if (op==2) {
			scanf("%d%d%d",&x,&y,&z);
			modify(rt[x],1,n,z,y);
		} else if (op==3) {
			scanf("%d%d%d",&x,&y,&z);
			printf("%lld\n",query(rt[x],1,n,y,z));
		} else if (op==4) {
			scanf("%d%d",&x,&y);
			if (val[rt[x]]<y) {printf("-1\n");continue;}
			printf("%d\n",kth(rt[x],1,n,y));
		}
	}
	return 0;
}