自动搬运

查看原文

来自洛谷，原作者为

	command_block 众水皆昂首，饮月唯我一。

搬运于2025-08-24 22:11:04，当前版本为作者最后更新于2019-08-09 19:45:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

很好的一到计算几何题目啊,怎么没人做qwq?

此外是用我的写法,这题并不卡精度……

前置芝士

• 判断一个点是否在简单多边形内

这个题要求在多边形边上也不算,那么先一通判定该点是否在某条边上。

然后过这个点随意做一条射线,如果与多边形有奇数个交点则在多边形内,否则在外面。

(为了避免恰好在多边形顶点处相交的情况,最好随机射线方向,或者设一个比较刁钻的值)

• 求线段与圆的交点

先求出直线与圆的交点,在判断是否在线段上即可。

具体求法:判断直线到圆心$O$的距离,如果相切或者相离则舍去。

设两个交点是$A_1,A_2$。

过圆心做直线的垂线,算出交点$M$,半径$r$和$OM$,$A_1M$组成直角三角形,那么勾股一下得到$A_1M$和$A_2M$。

在之后,把向量$\overrightarrow{MO}$的方向向量分别左转和右转$90$度,然后缩放$A_1M$倍,加上$M$,即可得到两个交点。

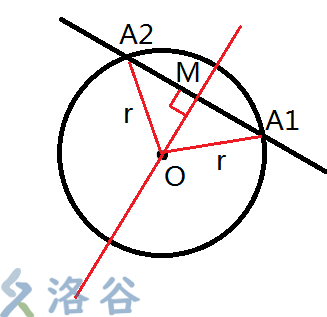
• 平分一段弧

利用垂径定理,作弦的垂线,求出垂线的方向向量,在缩放$r$倍即可恰好碰到圆周。

问题转化

这里每个点被覆盖到的概率是独立的,被根据期望的线性性,我们可以一个一个来算,最后再加起来。

那么问题就变成了:给出一个点和一个简单多边形,问在简单多边形随机旋转以后这个点有多少概率在多边形内。

与其让多边形转,不如让点转,那么问题又变成了:

给出一个点和一个简单多边形,问在点随机旋转以后这个点有多少概率在多边形内。

那么我们以原点为圆心,点到原点距离为半径,画一个圆,这就是那个点的运动轨迹。

这个圆弧在多边形内的长度除以2Pi就是答案。

解决方案

(假如这个点就是原点,那么形不成圆弧,直接判断该点是否在多边形内)

首先算出这个圆弧与多边形的所有交点。

如果没有交点,要么整个圆都在多边形外面,要么整个圆都在里面。

随意取圆上任意一点判断是否在多边形内即可。

如果有交点,就把这些交点极角排序,可以得到$O(m)$段弧,我们要一一判断这些弧在不在圆内。

如何判断?求出弧的重点,然后判断是否在多边形内即可这里的复杂度是$O(m)$。

那么这个题就做完了,总的复杂度$O(nm^2)$,有点松。

#include<algorithm>
#include<cstdio>
#include<cmath>
#define eps 1e-7
#define MaxN 1050
using namespace std;
const double Pi=acos(-1);
int sign(double x)
{return x>eps ? 1 : (x<-eps ? -1 : 0);}
struct Point
{
  double x,y,rt;
  Point operator + (const Point &B) const
  {return (Point){x+B.x,y+B.y};}
  Point operator - (const Point &B) const
  {return (Point){x-B.x,y-B.y};}
  Point operator * (const double &B) const
  {return (Point){x*B,y*B};}
  Point operator / (const double &B) const
  {return (Point){x/B,y/B};}
  double operator ^ (const Point &B) const
  {return x*B.y-y*B.x;}
  bool operator == (const Point &B) const
  {return sign(x-B.x)==0&&sign(y-B.y)==0;}
}p[MaxN];
bool cmp(Point A,Point B)
{return sign(A.rt-B.rt)<0;}
double dis(Point A,Point B)
{return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}
struct Line
{
  Point a,b;
  double len(){return dis(a,b);}
}l[MaxN];
bool onl2(Point A,Line L)
{
  return sign((A-L.a)^(A-L.b))==0&&
         sign(A.x-min(L.a.x,L.b.x))>=0&&
         sign(A.y-min(L.a.y,L.b.y))>=0&&
         sign(A.x-max(L.a.x,L.b.x))<=0&&
         sign(A.y-max(L.a.y,L.b.y))<=0;
}
bool _onl2(Point A,Line L)
{
  return sign(A.x-min(L.a.x,L.b.x))>=0&&
         sign(A.y-min(L.a.y,L.b.y))>=0&&
         sign(A.x-max(L.a.x,L.b.x))<=0&&
         sign(A.y-max(L.a.y,L.b.y))<=0;
}
Point inter(Line L1,Line L2)
{
  double ls=(L1.b-L1.a)^(L2.a-L1.a),
         rs=(L1.b-L1.a)^(L2.b-L1.a);
  return L2.a+(L2.b-L2.a)*ls/(ls-rs);
}
double disl0(Point A,Line L)
{return fabs((L.a-A)^(L.b-A))/dis(L.a,L.b);}
int m;
//判断点是否在简单多边形内
bool in(Point A)
{
  for (int i=1;i<=m;i++)
    if (onl2(A,l[i]))return 0;
  Line L=(Line){A,(Point){A.x+0.2333,A.y+0.6666}};
  int cnt=0;
  for (int i=1;i<=m;i++){
    Point B=inter(L,l[i]);
    if (sign(B.y-A.y)>0&&_onl2(B,l[i]))cnt++;
  }return cnt&1;
}
double _r[MaxN];
int n;
void input()
{
  scanf("%d%d",&n,&m);
  double x,y;
  for (int i=1;i<=n;i++){
    scanf("%lf%lf",&x,&y);
    _r[i]=sqrt(x*x+y*y);
  }
  for (int i=1;i<=m;i++)
    scanf("%lf%lf",&l[i].a.x,&l[i].a.y);
  for (int i=1;i<m;i++)
    l[i].b=l[i+1].a;
  l[m].b=l[1].a;
}
double ans;
Point bas=(Point){0,0},t[MaxN];
//判断一段弧是否在圆内
void check(Point A,Point B,double r)
{
  Point C=(B-A)/dis(A,B);
  C=(Point){-C.y,C.x}*r;
  //注意逆时针序
  if (in(C)){
    if (A.rt>B.rt)ans+=Pi*2;
    ans+=B.rt-A.rt;
  }
}
void solve(double r)
{
  if (sign(r)==0){
    if (in(bas))ans+=Pi*2;
    return ;
  }int tot=0;
  for (int i=1;i<=m;i++){
    if (disl0(bas,l[i])-r>-1e-3)continue ;
    Point C=(l[i].a-l[i].b)/dis(l[i].a,l[i].b);
    //C: l的方向向量
    Line ML=(Line){bas,(Point){-C.y,C.x}};
    //ML: l的垂线
    Point M=inter(ML,l[i]);
    double rl=sqrt(r*r-M.x*M.x-M.y*M.y);
    //勾股(垂径)定理
    C=C*rl;
    Point P1=M+C,P2=M-C;
    //直线与圆交点计算完毕
    if (_onl2(P1,l[i]))t[++tot]=P1;
    if (_onl2(P2,l[i]))t[++tot]=P2;
  }
  //特判整个圆在多边形内/外的特殊情况
  if (tot==0){
    Point B=(Point){0,r};
    if (in(B))ans+=2*Pi;
    return ;
  }
  for (int i=1;i<=tot;i++)
    t[i].rt=atan2(t[i].x,t[i].y);
  sort(t+1,t+tot+1,cmp);
  //极角排序
  for (int i=1;i<=tot;i++)
    if (!(t[i]==t[i%tot+1]))
      check(t[i],t[i%tot+1],r);
}
int main()
{
  input();
  for (int i=1;i<=n;i++)solve(_r[i]);
  printf("%.5lf",fabs(ans/Pi/2));
  return 0;
}