自动搬运

查看原文

来自洛谷，原作者为

	Lolierl **

搬运于2025-08-24 22:10:39，当前版本为作者最后更新于2019-07-23 11:29:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

USACO银组题目，照例还是比较灵活、巧妙的。

题意：一个01矩阵，每次翻转一行或一列，最后除了一个元素之外的其他元素完全一样，求这个元素。

乍一看似乎没什么思路。怎么下手呢？

首先我们注意到，0和1是对称的，也就是说因为不限次数，只需把每一行翻转一遍就可以把元素01互换。

于是我们先把第一行和第一列翻转成0。

方法：对于第一行中的1，翻转它所在的列；对于第一列中的1，翻转它所在的行。

于是我们得到了一个新矩阵：(以5*5为例）

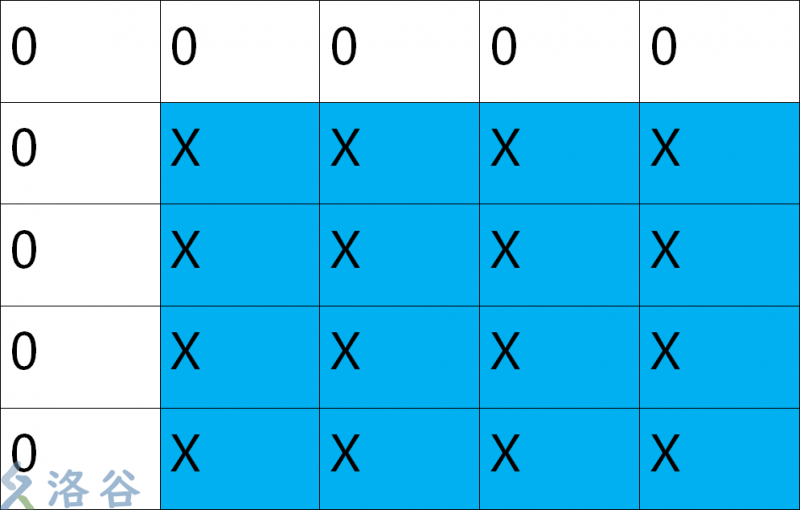
于是我们发现：在不改变第一行和第一列的情况下，蓝色部分无法被改变（因为两次翻转同一行等于没有翻转）。

若有解，则解只有以下三种位置：（1，1）、第一行或第一列（除（1，1）外）、蓝色区域中

若答案在蓝色区域中，目标位置此时一定为1并且其他部分全部为0

若答案在（1，1），则蓝色区域一定此时全部为1（翻转第一行再翻转第一列后，图中只有（1，1）为0）

若答案在第一行或第一列（除（1，1））上，则目标位置所在列或行在蓝色区域中一定全部为1且蓝色区域其他部分全部为0（翻转该列或行后，图中只有目标位置为1）

若不符合这三种情况，则无解

（感性理解一下没有其他情况吧qwq，蒟蒻也不会严谨证明啊）

于是我们就愉快地做完了

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector> 
#define pii pair<int, int>
using namespace std; 

int main()
{
	int n; 
	scanf("%d", &n); 
	if(n == 1){printf("-1"); return 0; }
	
	char c; 
	int a[n + 1][n + 1]; 
	
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
		{
			c = getchar(); 
			while(c != 'L' && c != 'R')c = getchar(); 
			a[i][j] = ((c == 'L') ? 0 : 1); 
		}
	
	for(int i = 1; i <= n; i++)
		if(a[i][1])
			for(int j = 1; j <= n; j++)
				a[i][j] ^= 1; 
	
	for(int i = 2; i <= n; i++)
		if(a[1][i])
			for(int j = 1; j <= n; j++)
				a[j][i] ^= 1; 
	//翻转			
	int f = 0; 
	for(int i = 2; i <= n; i++)
		for(int j = 2; j <= n; j++)
			f += a[i][j]; 
	//通过子矩阵和判断情况
	if(f == (n - 1) * (n - 1))
	{
		if(n == 2)printf("-1\n"); else printf("1 1\n"); 
		return 0; 
	}
	else if(f == 1)
	{
		for(int i = 2; i <= n; i++)
			for(int j = 2; j <= n; j++)
				if(a[i][j]){printf("%d %d", i, j); return 0; }
	}
	else if(f == n - 1)
	{
		for(int i = 1; i <= n; i++)
		{
			int s = 0; 
			for(int j = 1; j <= n; j++)
				s += a[i][j]; 
			if(s == n - 1){printf("%d %d", i, 1); return 0; }
		}
		for(int i = 1; i <= n; i++)
		{
			int s = 0; 
			for(int j = 1; j <= n; j++)
				s += a[j][i]; 
			if(s == n - 1){printf("%d %d", 1, i); return 0; }
		}
	}//三种情况
	printf("-1"); 
	return 0; 
} 

有错误请指出qwq