自动搬运

查看原文

来自洛谷，原作者为

	Time_tears oi复健ing

搬运于2025-08-24 22:10:36，当前版本为作者最后更新于2020-09-11 14:59:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本题是一道很好的轮廓线 Dp，希望这篇题解能对你有所帮助，点个赞吧。

直接进入正题，我们怎么来考虑轮廓线我们设 $f_{s}$ 表示最下面的连通情况 。

首先我们初始化第 $0$ 行，这一部分就只需要枚举一个 $O(2^{3*n } )$ 的状态 $s$ ，把 $s$ 的最小连通情况 (连通块从零开始编号)（这里连通块一定是相邻的，所以直接算）表示出来后，我们就可以开始 Dp 了。

我们考虑怎么转移到 $i,j$ ，有这么几种情况：

1. $j=0$

这里又可以分为两种情况

$<1>$ 继承上一行的衣钵：$(shu_{i,j})$ 的贡献

$<2>$ 我自立山头：$(0)$ 的贡献（自立山头是把新连通块当成 $6$，反正后面会处理，这里不慌。同时，自立山头有一个前提：上一行已经和其他点连通了，要不然 $i-1,j$ 这个点就被抛弃了 )

2. $j>0$

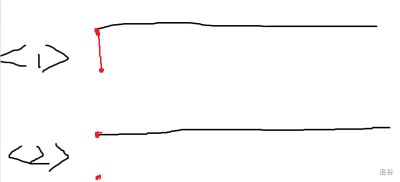
$<1>$ 还是继承上一行的衣钵： $(shu_{i,j})$ 的贡献

$<2>$ 我自立山头： $(+0)$ 的贡献

$<3>$ 把我加入 $i,j-1$ 的连通块： $(heng_{i,j})$ 的贡献

$<4>$ 靠我把 $i,j-1$ 和 $i-1,j$ 给连起来： $(shu_{i,j}+heng_{i,j})$ 的贡献

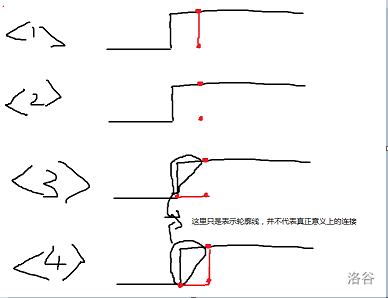
然后就是一些实现上面的细节，假如我们每次都要算状态复杂度直接爆炸，所以我们直接预处理并记忆化状态，这样就好办很多（ $CSH$ 函数），然后初始与 $s$ 有关的状态 （$Calc$ 函数），然后注意一下细节就可以了。$：)$

代码一定不要抄噢。

#include<cstdio>
#include<iomanip>
#include<cstring>
#define N 30005
#define M (1<<18)+5
#define ll long long
#define mod 1000000007
#define O4 __inline__ __attribute__((always_inline))
using namespace std;
int las=1,cnt[M][7],tr[M][7];
int n,k,now,he[N][7],su[N][7],vis[M];
const int Mxdt=180000;
O4 char gc() {
	static char buf[Mxdt],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,Mxdt,stdin),p1==p2)?EOF:*p1++;
}
O4 int read() {
	int res=0,bj=0;
	char ch=gc();
	while(ch<'0'||ch>'9')bj|=(ch=='-'),ch=gc();
	while(ch>='0'&&ch<='9')res=(res<<3)+(res<<1)+(ch^48),ch=gc();
	return bj?-res:res;
}
O4 int Mod(int x) {
	return x<=mod?x:x-mod;
}
struct at {
	ll val;
	int cnt;
	at() {
		val=1e18,cnt=0;
	} at(ll _v,int _c):val(_v),cnt(_c) {}
};
O4 at operator *(at a,at b) {
	return (a.val!=b.val)?(a.val<b.val?a:b):(at(a.val,Mod(a.cnt+b.cnt)));
}
O4 at operator +(at a,ll b) {
	return at(a.val+b,a.cnt);
}
struct Node {
	pair<at,bool>val[M];
	int s[M],top;
	Node() {}
	O4 void clear() {
		for(int i=1; i<=top; ++i)val[s[i]].second=0;
		top=0;
	}
	at &operator[](int x) {
		if(!val[x].second)val[x]=make_pair(at(),1),s[++top]=x;
		return val[x].first;
	}
} dp[2];
O4 void Init(ll val=0) {
	for(int st=0,s=0,ct=0; st<(1<<k-1); dp[now][s]=at(val,1),++st,s=ct=val=0)
		for(int t=1; t<k; ++t)((st&(1<<t-1))?val+=he[0][t]:++ct),s|=ct<<(t*3);
}
O4 int Get(int s,int x) {
	return (s>>3*x)&7;
}
O4 int Change(int s,int x,int y) {
	return s^((Get(s,x)^y)<<3*x);
}
O4 void Work(int s,int x) {
	for(int i=0; i<k; ++i)
		if(Get(s,i)==x&&++cnt[s][x]>1)return;
}
O4 void CSH(int s) {
	if(vis[s])return;
	static int cnt,tmp,id[7];
	memset(id,-1,sizeof(id)),cnt=0,tmp=s;
	for(int i=0,x; i<k; ++i)x=Get(s,i),s=Change(s,i,(~id[x])?id[x]:id[x]=cnt++);
	return vis[tmp]=s,void();
}
O4 void Merge(int s,int x) {
	int t1=Get(s,x-1),t2=Get(s,x),tmp=s;
	if(t1==t2)return tr[tmp][x]=s,void();
	for(int i=0; i<k; ++i)if(Get(s,i)==t2)s=Change(s,i,t1);
	tr[tmp][x]=s;
}
O4 void Calc(int s) {
	static int vis[M]= {0};
	if(vis[s])return;
	vis[s]=1,CSH(s);
	for(int i=0; i<k; ++i)CSH(Change(s,i,6));
	for(int i=1; i<k; ++i)Merge(s,i),CSH(tr[s][i]);
	for(int i=0; i<k; ++i)Work(s,i);
	for(int i=1; i<k; ++i)CSH(Change(s,i,Get(s,i-1)));
}
O4 void Update(int s,at x) {
	dp[now][vis[s]]=dp[now][vis[s]]*x;
}
int main() {
	n=read(),k=read();
	for(int i=0; i<n; ++i)for(int j=1; j<k; ++j)he[i][j]=read();
	for(int i=0; i<k; ++i)for(int j=1; j<n; ++j)su[j][i]=read();
	Init();
	for(int i=1; i<n; ++i)
		for(int j=0,x; j<k; ++j) {
			now^=1,las^=1,dp[now].clear();
			for(int t=1,s; t<=dp[las].top; ++t) {
				at atom=dp[las][s=dp[las].s[t]];
				if(Calc(s),!j) {
					Update(s,atom+su[i][j]);
					if(cnt[s][Get(s,j)]>1)Update(Change(s,j,6),atom);
				} else {
					Update(s,atom+su[i][j]);
					if(cnt[s][Get(s,j)]>1)Update(Change(s,j,Get(s,j-1)),atom+he[i][j]),Update(Change(s,j,6),atom);
					if(Get(s,j)!=Get(s,j-1))Update(tr[s][j],atom+(su[i][j]+he[i][j]));
				}
			}
		}
	printf("%d\n",dp[now][0].cnt);
	return 0;
}