自动搬运

查看原文

来自洛谷，原作者为

	KAMIYA_KINA 近若咫尺，却邈以山河

搬运于2025-08-24 22:10:35，当前版本为作者最后更新于2021-10-17 21:08:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Tag

构造。

Description

你需要构造一个 $n$ 阶完全图，使得其最大上升路径长度最小。

$\texttt{data range:} n\leq 500$，保证 $n$ 是偶数.

Solution

非常好玩的构造题，看了鱼大的题解之后又学到了新知识呢！

先给出题面中的一个证明，对于一个带权无向完全图而言，一共有 $2n$ 个点，其有 $n(2n-1)$ 条边，每个点上放一个人，然后将边从小枚举到大，每次交换两个点上的人，那么所有人一共走了 $2n(2n-1)$ 步，所以一个人就走了 $(2n-1)$ 步，然后这 $(2n-1)$ 步就是答案的下界了。

现在的问题是我们需要构造一个完全图来达到这个下界，接下来的内容大多是鱼大的方法给的启发。

考虑一个完全图的生成子图 $H$ 是 $k-$正则的，即为这个生成子图中所有点的度数为 $k$，那么我们称这个生成子图 $H$ 是 $G$ 的一个 $k-$因子。

特殊地，$G$ 的一个 $1-$因子就是这个图的一个完美匹配。（根据定义即可证明）

那么给出一个非常显然的结论：偶数阶完全图 $K_{2n}$ 一定存在 $1-$因子分解。

而且一个 $1-$因子一定是只有 $n$ 条边，那么这个完全图 $K_{2n}$ 一定可以分解成 $2n-1$ 个 $1-$因子。（因为他有 $n(2n-1)$ 条边嘛）

我们惊讶的发现这个东西的数值跟答案的下界一样，所以我们就可以想办法去构造这 $2n-1$ 个 $1-$因子，然后保证这 $2n-1$ 个因子中第 $i$ 个当中的值严格小于第 $i+1$ 个就可以了。

思考这样为什么是对的，根据 $1-$因子的定义，这个生成子图中点度数为 $1$，所以通过了一条第 $i$ 个 $1-$因子的边后，不可能再次达到第 $i$ 个 $1-$因子的点，这是显然的，所以只能往更高的 $1-$因子转移，但是整体的 $1-$因子个数是 $2n-1$ 个，所以肯定不会上升超过 $2n-1$ 次，证毕。

接下来思考如果构造。

我们将这 $2n$ 个点分成两部分，第一部分是 $2n-1$ 个正多边形围在最外圈，最后一个点放在里面，之后就可可以螺旋构造很容易构造了。每个 $1-$因子就是将中间这个点连到周围的 $2n-1$ 个点其中一个上，然后其他的点与中心点连的这条边垂直就可以了，具体可以看下图，是 $n=4$ 时的一种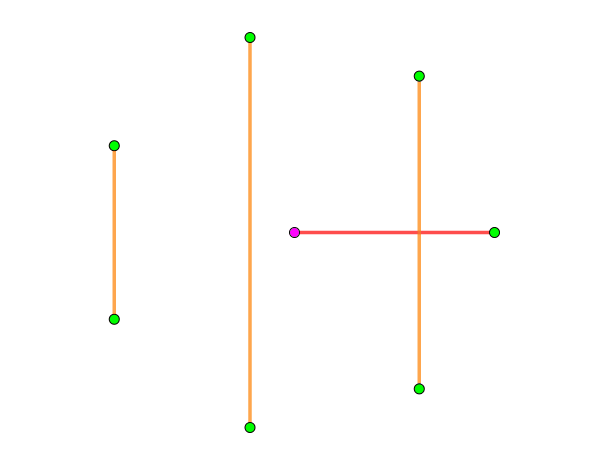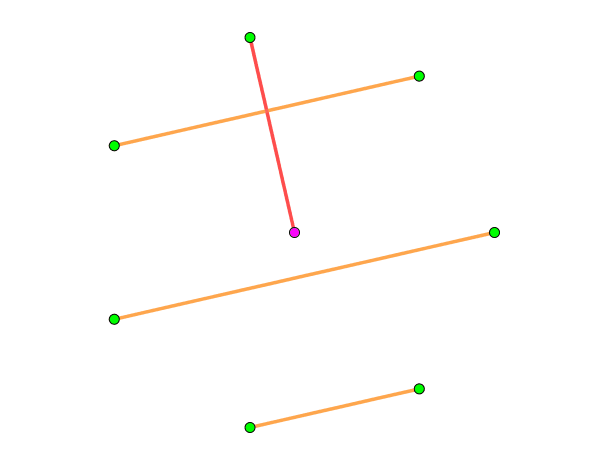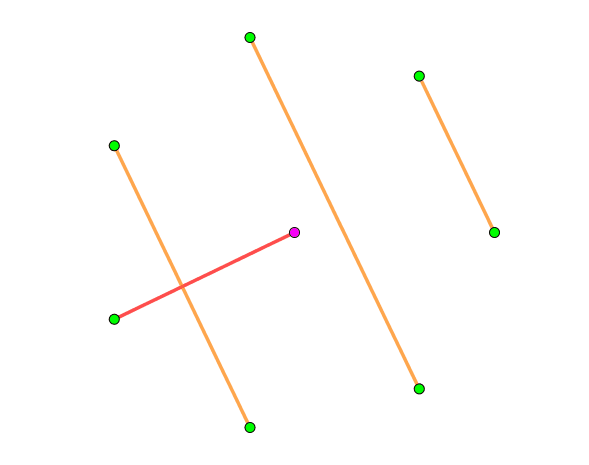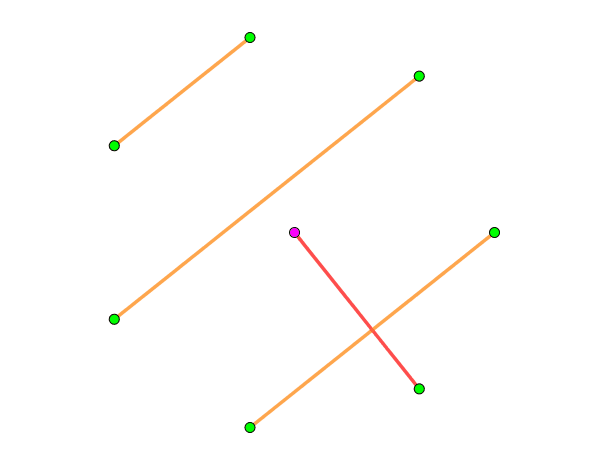构造：

（从鱼大那里蒯的，图床崩了的话可以点一下去原地址看）

然后直接做就可以了。

时间复杂度 $O(n^2)$.

Code

const int N = 5e2 + 1;

int g[N][N];

inline void solve() {
    int n = rd - 1, w = 0;//钦定第 n 个点为放到中间的那个点
    for(int i = 0; i < n; i++) {
        g[i][n] = g[n][i] = ++w;
        for(int j = 1; j <= n >> 1; j++) {//螺旋构造转转转
            int u = (i - j + n) % n, v = (i + j) % n;
            g[u][v] = g[v][u] = ++w;
        }
    }
    for(int i = 0; i < n; i++)
        for(int j = i + 1; j <= n; j++)
            cout << g[i][j] << (j == n ? '\n' : ' ');
    return ;
}

Final

本来是想要做另一道题来着，然后看到鱼大的题解里面放了这一题的链接，以为是前置知识什么的，发现那题比这题简单多了。