自动搬运

查看原文

来自洛谷，原作者为

	lonlyn **

搬运于2025-08-24 22:10:18，当前版本为作者最后更新于2019-08-06 12:00:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

可能在博客里内容更丰富一些

  10%的数据：打表状压dp。

  30%的数据：非常朴素的状压dp+矩阵加速。

  50%的数据：虽然方案数 $2^{11}$ 比较多，但是真正可行的方案只有199种。我们只需针对可行的方案进行处理，便可以在时间空间上得以满足。（如果发现因为tle得了30分大概需要卡一卡常数反正我卡了）

  50分代码自动省略（大佬们应该都会虽然博客里有）。

  100%数据：

  当x为17的时候我们发现可行的方案数也达到 3571 让人无法接受。所以我们要减少方案。

  方法就是将类似的方案合并，也就是将能循环互相得到的方案归到一组，成为一个总的状态，用它进行转移。

  为什么可以这么做？

  对于两组状态 $A,B$ ，我们现在要求由 $A$ 状态转移到 $B$ 状态，对于任意的两个状态 $s1,s2\in{A}$ ，它转移到B状态的方案数是相同的。

  证明？显然因为这是个可以循环的结构。我们完全可以把s2旋转到s1的位置重合（属于一个方案组），同样s2时的B中状态也同时旋转到与s1时的B中状态相同。所以是等价的。

  （这个道理不好说明可以意会一下。下面有图片解释）

  通过分组思维我们就可以将方案数减少到 211 种，然后就可以解决此题。

  同时记录一下几个坑：

  1.注意全0方案的处理。全0方案自成一组，它到任何方案组的方案数为其方案组里的状态总数，任何方案组到全0方案组的的方案数为 1 。

  2.方案组可以转移到方案组自身。且注意此时方案数不一定为方案组里状态总数-1。

  3.方案组里的状态总数并不一定等于 x 。

  最后再来个方案组等价举例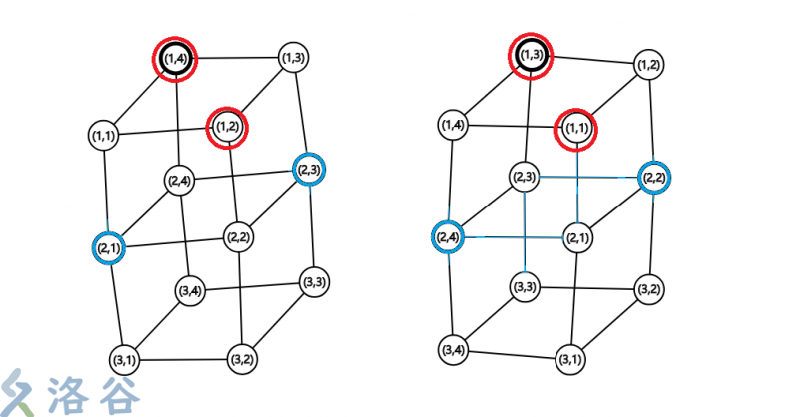：   如图，第一层（红色）左右两个状态等价。它们转移到第二层（蓝色）的可选点也就是蓝色标出的点，旋转后即相同。

  完结撒花。蒟蒻代码如下:

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<ctime>
#include<vector>
using namespace std;
#define ll long long
#define il inline
#define rg register
const ll mod=998244353;
struct matrix{
    ll a[233][233];
    void clr(){
        memset(a,0,sizeof(a));
    }
}u,v,ed;
ll n,x,ans;
int a_id[132000],tot;
int num[20]; int p;
int s[132000],vis[132000];
vector<int> G[132000];
il matrix unit(){
    matrix tmp; tmp.clr();
    for (rg int i=1;i<=230;++i)
      tmp.a[i][i]=1;
    return tmp;
}
il matrix operator * (matrix aa,matrix bb){
    matrix tmp; tmp.clr();
    for (rg int k=1;k<=tot;++k){
        for (rg int i=1;i<=tot;++i){
            for (rg int j=1;j<=tot;++j){
                tmp.a[i][j]=((tmp.a[i][j]+aa.a[i][k]*bb.a[k][j]))%mod;
            }
        }
    }
    return tmp;
}
il int work(int tmp){
    if (tmp&(1<<x)) return tmp-(1<<x)+1;
    else return tmp;
}
il void checkcircle(int tmp){
    G[tmp].push_back(tmp);
    a_id[++tot]=tmp;
    s[tmp]++; vis[tmp]=1;
    int nxt=work(tmp<<1);
    while (!vis[nxt]){
        G[tmp].push_back(nxt);
        vis[nxt]=true; s[tmp]++;
        nxt=work(nxt<<1);
    }
}
il void check(int tmp){
    if (vis[tmp]) return;
    int xx=tmp;
    p=0; memset(num,0,sizeof(num));
    while (tmp){
        ++p;
        if (tmp&1) num[p]=true;
        tmp>>=1;
    }
    for (rg int i=2;i<=x;++i)
      if (num[i]&&num[i-1]) return;
    if (num[x]&&num[1]) return;
    checkcircle(xx);
    u.a[tot][tot]=s[a_id[tot]];
}
il void link(){
    for (rg int i=1;i<=tot;++i){
        for (rg int j=1;j<=tot;++j){
            int uu=a_id[i],vv=a_id[j],sum=0,to;
            if (vv==0){
                v.a[i][j]=1;
                continue;
            }
            if (uu==0){
                v.a[i][j]=s[vv];
                continue;
            }
            for (rg int k=0;k<G[vv].size();++k){
                to=G[vv][k];
                if ((uu&to)==0) ++sum;
            }
            v.a[i][j]=sum;
        }
    }
}
int main(){
    cin>>n>>x;
    for (rg int i=0;i<=(1<<x)-1;++i) check(i);
    link();
    matrix tmp=unit(); n--;
    while (n){
        if (n&1) tmp=tmp*v;
        v=v*v; n>>=1;
    }
    ed=u*tmp;
    for (rg int i=1;i<=tot;++i)
      for (rg int j=1;j<=tot;++j){
        ans=(ans+ed.a[i][j]+mod)%mod;
    }
    cout<<ans;
    return 0;
}

对蒟蒻我来说这题感觉真的很鲁棒