自动搬运

查看原文

来自洛谷，原作者为

	_awa_wangjiawen 退役倒计时：71day

搬运于2025-08-24 22:10:09，当前版本为作者最后更新于2025-08-19 15:02:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

在一个圆上给出 $n$ 个点两两相连最多能分成几块区域。

思路

平面上，一条线与 $x$ 条线相交，就会多分割出 $x+1$ 块区域。（可简单试验证明得）

尝试用递推的方法，从已给出 $n-1$ 个点推出给出 $n$ 个点。

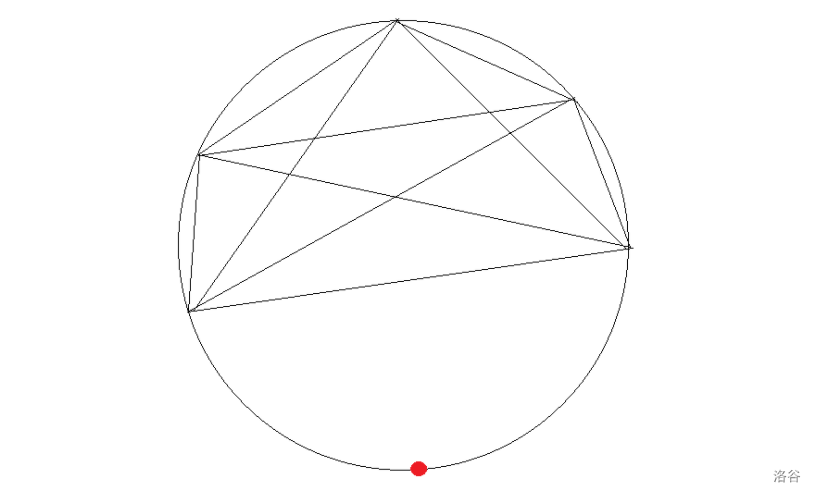
当我们加入第 $n$ 个点时，将其与其他 $n-1$ 个点连线，然后把每条线拿出来单独看。

单独看一条线，它会把圆分割成两个区域（这里称为 $A$ 和 $B$）。$A$ 和 $B$ 中的点需要两两相连，一定会与这条线相交，所以这条线会与 $|A| \times |B|$ 条线相交，也就会多分割出 $|A| \times |B| + 1$ 块区域。（这里 $|A|$ 指 $A$ 中点的个数）

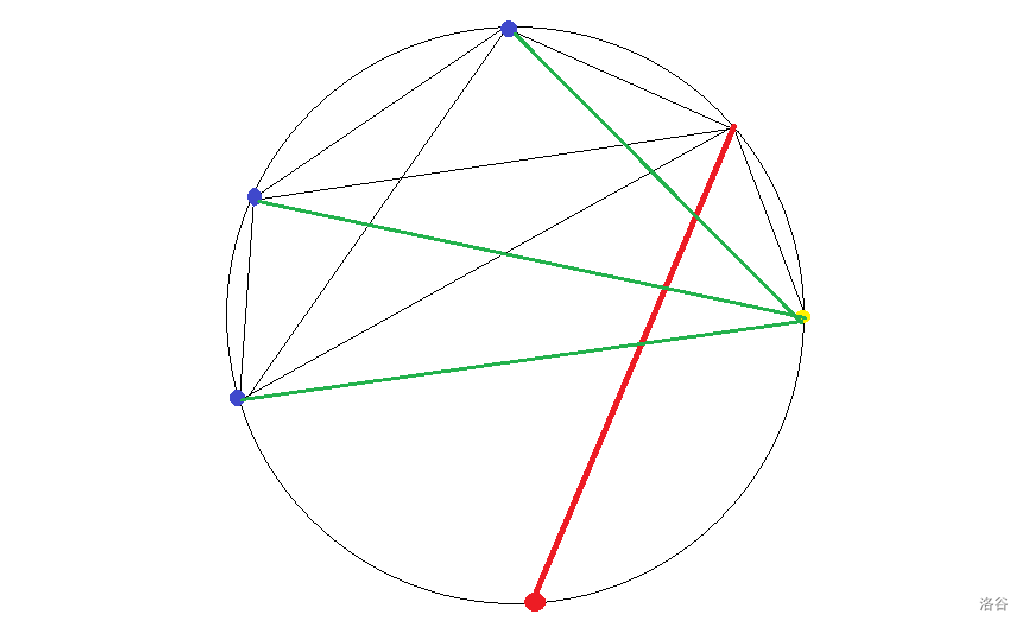
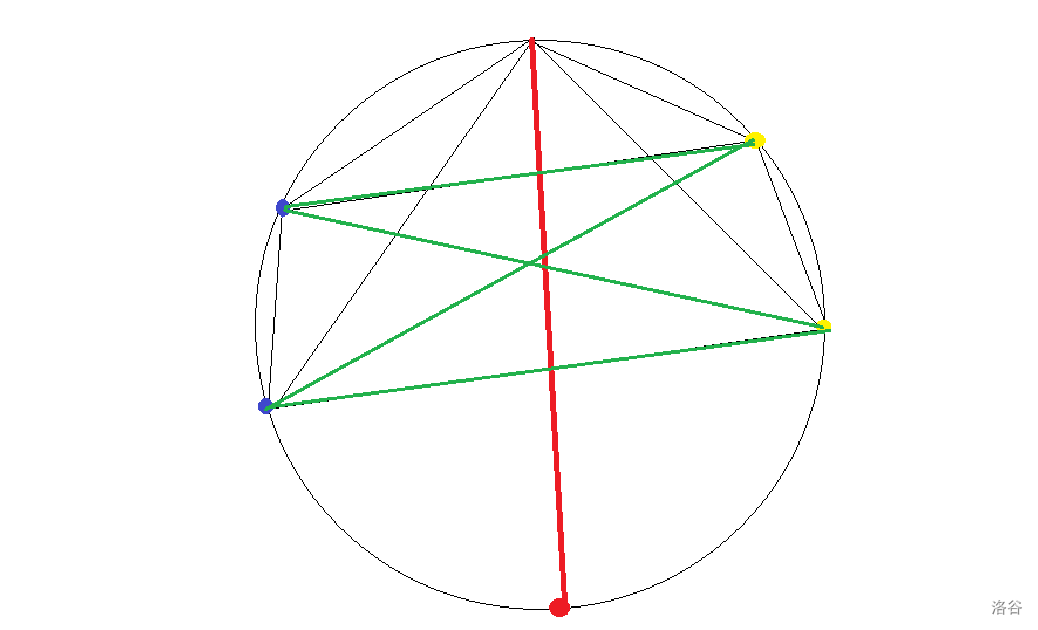
代码

#include<bits/stdc++.h>
using namespace std;
const long long mod1=998244353;
const long long mod2=1000000007;
const long long inf=0x3f3f3f3f3f3f3f3f;
long long ans[101];
long long n;

void init();
void domemset();
long long read();
void write(long long x);


void fun()
{
//	domemset();
	write(ans[max(0ll,n-1)]);
	putchar('\n');
	return ;
}


int main()
{
	init();
//	t=read();
//	for(int i=1;i<=t;i++)
//	while(1)
	while(cin>>n)
		fun();
	return 0;
}
void init()
{
	ans[0]=1;
	for(int i=1;i<=64;i++)
	{
		ans[i]=ans[i-1];
		for(int j=0;j<=i-1;j++)
			ans[i]=ans[i]+j*(i-1-j)+1;
	}
	return ;
}
void domemset()
{

	return ;
}
long long read()
{
	long long x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<3)+(x<<1)+(ch^'0');
		ch=getchar();
	}
	return x*f;
}
void write(long long x)
{
	if(x<0)
		putchar('-'),x=-x;
	if(x>=10)
		write(x/10);
	putchar((x%10)^'0');
	return ;
}